Классификция. Задача классификации

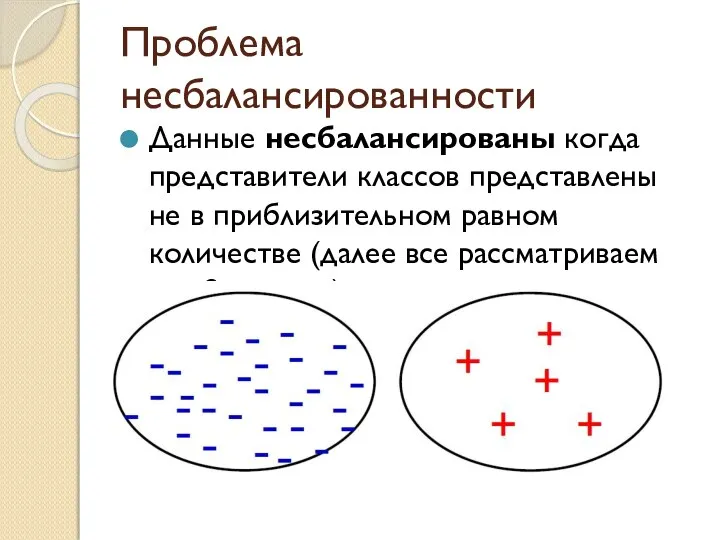
Проблема несбалансированности
Данные несбалансированы когда представители классов представлены не в приблизительном равном количестве (далее все рассматриваем для 2 классов)

В чем проблема?
Многие стандартные классификаторы пытаются увеличить точность и не изменить распределение обучающей выборки, поэтому они игнорируют маленькие классы. Если данные не сбалансированы, то предсказание большего класса для любого объекта приводит к точности порядка 90% (в зависимости от соотношения классов)

Цель классификации - детектирование
Стоимость ошибки неправильно классифицировать ненормальный образец данных как нормальный много выше чем наоборот.
Пример - поиск раковых клеток среди здоровых

Примеры несбалансированных данных:
1) из 100 000 тысяч подавших заявку, только 2% проходят в гарвард на стажировку
2) автоматизированная машина проверяющая на дефект произведенные на конвейере продукты намного чаще выбирает продукт без дефекта
3) тест на проверку заболевания раком получает в результатах много больше здоровых людей чем больных
4) в отслеживании воровства кредитных карт законных переводов много больше чем незаконных
5)мошеннические телефонные звонки
6)обнаружение нефтяных пятен по изображениям со спутника
7)оценка рисков

Техники работы с несбалансированными данными
I. Работа с данными :
SMOTE
Random Undersampling
Random Oversampling
II.Чувствительность к стоимости ошибки
III. Выбор характеристик

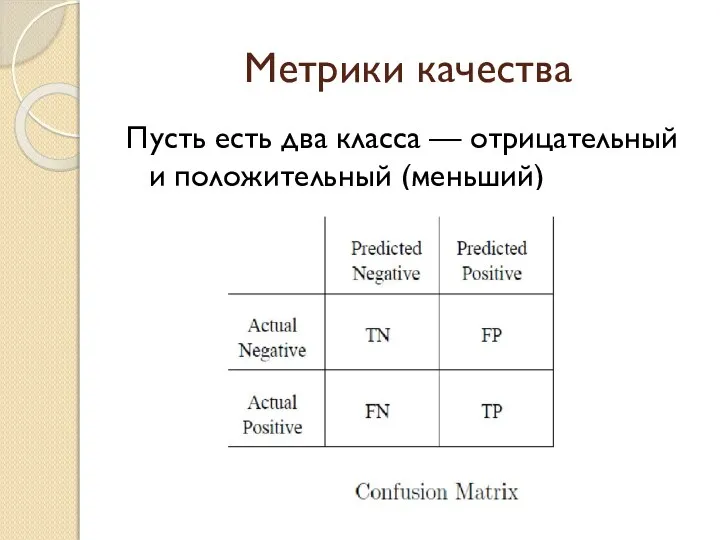
Метрики качества
Пусть есть два класса — отрицательный и положительный (меньший)

1) Accuracy – для сбалансированных данных
Процент правильно классифицированных образцов от всего числа образцов

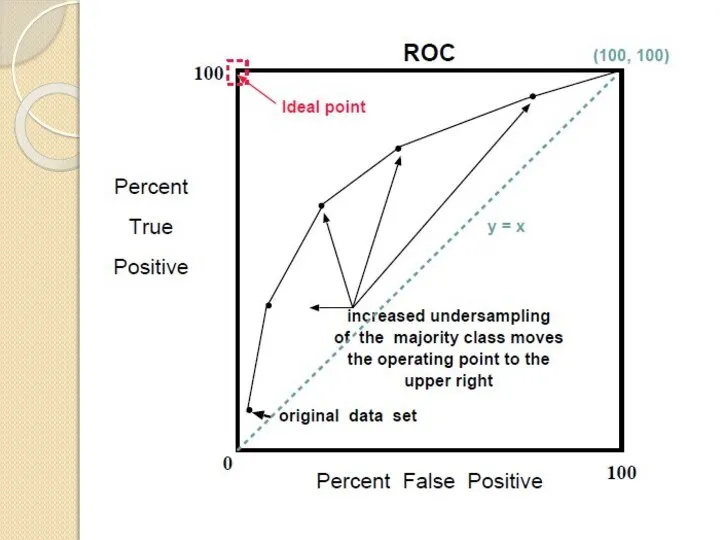
2) ROC кривая – для несбалансированных
представляет границы лучших решений для относительных TP (по оси У) & FP(по оси Х)
каждая точка — классификатор с какими-то параметрами
линия х=у — при произвольном выборе метки класса

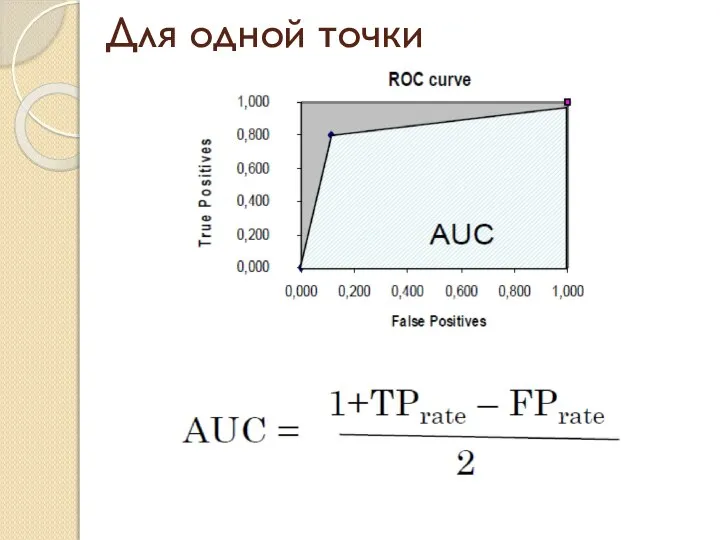
AUC - площадь под ROC кривой .
Она эквивалентна вероятности того что классификатор ценит произвольно выбранный образец меньшего класса выше чем произвольно выбранный образец из большего класса. (она больше 0,5)
Т.е. это численная характеристика для сравнения классификаторов

Для одной точки

Преимущества ROC
Когда алгоритм изучает больше образцов одного (-) класса он будет ошибочно классифицировать больше образцов другого класса (+). т.о. ROC изображает согласование между долей правильных и долей ложных предсказаний классификатора.
ROC показывает в каком диапазоне (в нашем случае соотношений обьемов классов) классификатор лучше других
ROC кривые нечувствительны к распределению по классам т. е. если соотношение между образцами из меньшего и большего класса изменится ROC кривая не изменится

Алгоритм SMOTE
Считываем число образцов меньшего класса Т
Процент генерируемых образцов N
Число ближайших соседей k
Для каждого образца (i) (вектора из атрибутов) из T(меньшего класса ) находим k ближайших соседей и генерируем [N/100] исскуственных образцов, повторяя на каждом шаге:
Из найденных соседей произвольно выбираем одного (nn), прибавляем к каждому из атрибутов i разницу между соответсвующими атрибутами i и nn, умноженную на произвольное число из отрезка [0,1] – получили новый вектор атрибутов – это новый искуственный образец меньшего класса
(атрибуты здесь – непрерывные величины,
т.е. числа)

SMOTE

Преимущества SMOTE
Этот способ увеличения меньшего класса не приводит к переобучению (в отличие от random oversampling), т. е. алгоритм одинаково хорошо работает и на новых данных.
Множественные примеры с различным распределением данных и соотношением представителей классов показывают, что SMOTE работает лучше
Не требует инициализации каких-либо величин, что сильно влияло бы на результат классификации
Недостатки SMOTE
Данный алгоритм не выходит за рамки существующих образцов меньшего класса, т.е. не будут созданы образцы с существенно отличными атрибутами, что вполне возможно в настоящих данных

Модификации SMOTE для дискретных атрибутов образцов
При вычислении атрибутов генерируемого образца для номинальных атрибутов значением будут самые частые соответсвующие номинальные атрибуты среди k ближайших соседей и рассматриваемого образца
SMOTE-NC