- Главная
- Математика
- Lektsia_1

Содержание
- 2. Метрология - наука о весах и мерах. Государственный стандарт (РМГ 29-2013 «Государственная система обеспечения единства измерений.
- 3. наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности Предмет изучения
- 4. Задачи метрологии Метрология как наука решает следующие основные задачи: – развитие общей теории измерений, установление единиц
- 5. Метрология В современном понимании метрология делится на теоретическую, к которой относят решение первых из перечисленных задач,
- 6. Роль метрологии В настоящее время измерения являются основой для нормальной работы любого предприятия или научно-исследовательского учреждения.
- 7. Основные понятия физическая величина : одно из свойств физического объекта, в качественном отношении общее для многих
- 8. Основные понятия Единство измерений – состояние измерений, при котором их результаты выражены в узаконенных единицах и
- 9. Основные понятия принцип измерений: Явление материального мира, положенное в основу измерения. Примеры 1 Применение эффекта Джозефсона
- 10. Основные понятия результат (измерения величины): Множество значений величины, приписываемых измеряемой величине вместе с любой другой доступной
- 11. Основные понятия 1 Для измерения, в котором имеют место повторные показания, каждое показание может использоваться, чтобы
- 12. Основные понятия погрешность (результата измерения): Разность между измеренным значением величины и опорным значением величины. Погрешность измерения
- 13. Основные понятия истинное значение (величины): Значение величины, которое соответствует определению измеряемой величины. Под истинным значением физической
- 14. Основные понятия опорное значение (величины): Значение величины, которое используют в качестве основы для сопоставления со значениями
- 15. Основные понятия случайная погрешность (измерения): Составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) при
- 16. Основные понятия доверительные границы (погрешности измерения): Верхняя и нижняя границы интервала, внутри которого с заданной вероятностью
- 17. Неопределенности измерений неопределенность (измерений): Неотрицательный параметр, характеризующий рассеяние значений величины, приписываемых измеряемой величине на основании измерительной
- 18. Погрешности измерения Границы относительной погрешности в долях или процентах находят из отношений: где — границы абсолютной
- 19. Понятие о физических величинах и системах единиц Под физической величиной понимается свойство, общее в качественном отношении
- 20. Понятие о физических величинах и системах единиц Все остальные величины и единицы определяются однозначно через основные
- 21. Основные и дополнительные единицы СИ
- 23. Скачать презентацию
Слайд 2Метрология - наука о весах и мерах.
Государственный стандарт (РМГ 29-2013 «Государственная система
Метрология - наука о весах и мерах.
Государственный стандарт (РМГ 29-2013 «Государственная система

Метрология – это наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.
Термин «метрология» произошел от греческого metron — мера и logos — учение, слово.
Основные направления метрологии:
общая теория измерений; единицы физических величин и их системы; методы и средства измерений; методы определения точности измерений; основы обеспечения единства измерений и единообразия средств измерения; эталоны и образцовые средства измерений; методы передачи размеров единиц от эталонов и образцовых средств измерений рабочим средствам измерений.
Слайд 3наука об измерениях, методах и средствах обеспечения их единства и способах достижения
наука об измерениях, методах и средствах обеспечения их единства и способах достижения

Предмет изучения метрологии — методы и средства, позволяющие проводить учет продукции, исчисляющейся по массе, длине, объему, расходу, мощности, энергии;
измерения для контроля и регулирования технологических процессов и для обеспечения функционирования транспорта и связи;
Измерения физических величин, технических параметров, состава и свойств веществ, проводимые при испытаниях и контроле продукции.
Слайд 4Задачи метрологии
Метрология как наука решает следующие основные задачи:
– развитие общей теории
Задачи метрологии
Метрология как наука решает следующие основные задачи:
– развитие общей теории

– разработка методов и средств измерений, способов определения точности измерений;
– обеспечение единства измерений и единообразия средств измерений, установление эталонов и образцовых средств измерений;
– разработка методов передачи размеров единиц от эталонов и образцовых средств рабочим средствам измерений.
Слайд 5Метрология
В современном понимании метрология делится на теоретическую, к которой относят решение первых
Метрология
В современном понимании метрология делится на теоретическую, к которой относят решение первых

РМГ 29-2013:
теоретическая метрология (theoretical metrology): Раздел метрологии, предметом которого является разработка фундаментальных основ метрологии.
законодательная метрология (legal metrology): Раздел метрологии, предметом которого является установление обязательных технических и юридических требований по применению единиц величин, эталонов, методов и средств измерений, направленных на обеспечение единства и требуемой точности измерений.
практическая (прикладная) метрология (practical (applied) metrology): Раздел метрологии, предметом которого являются вопросы практического применения разработок теоретической метрологии и положений законодательной метрологии.
Слайд 6Роль метрологии
В настоящее время измерения являются основой для нормальной работы любого предприятия
Роль метрологии
В настоящее время измерения являются основой для нормальной работы любого предприятия

Измерения нужны не только в технике. Успехи и темпы развития естественных наук самым непосредственным образом зависят от состояния измерительной техники. Без преувеличения можно утверждать, что бурное развитие естественных наук за последнее столетие целиком обусловлено столь же стремительным развитием измерительной техники, созданием современных и высокоточных средств измерений.
История науки знает немало примеров, когда успехи в области измерений служили основой научно-технического прогресса. Например, повышение точности измерения плотности воды привело в 1932 году к открытию тяжелого изотопа водорода – дейтерия, ничтожное содержание которого в обычной воде увеличивает ее плотность. При создании теории относительности Альбертом Эйнштейном использовались результаты эксперимента Майкельсона, который на основании тщательных измерений показал, что отсутствует смещение интерференционной картины при взаимном движении источника и приемника света.
Слайд 7Основные понятия
физическая величина : одно из свойств физического объекта, в качественном отношении
Основные понятия
физическая величина : одно из свойств физического объекта, в качественном отношении

измерение (величины): Процесс экспериментального получения одного или более значений величины, которые могут быть обоснованно приписаны величине. Измерение подразумевает сравнение величин или включает счет объектов. Измерение предусматривает описание величины в соответствии с предполагаемым использованием результата измерения, методику измерений и средство измерений, функционирующее в соответствии с регламентированной методикой измерений и с учетом условий измерений.
объект измерения: Материальный объект или явление, которые характеризуются одной или несколькими измеряемыми и влияющими величинами. Пример — Вал, у которого измеряют диаметр; технологический процесс, во время которого измеряют температуру; спутник Земли, координаты которого измеряются или с помощью которого измеряют координаты местоположения объекта на Земле. Это все объекты измерения.
Слайд 8Основные понятия
Единство измерений – состояние измерений, при котором их результаты выражены в
Основные понятия
Единство измерений – состояние измерений, при котором их результаты выражены в

Единство измерений обеспечивается их свойствами:
Сходимость результатов измерений – это близость результатов измерений, полученных одним и тем же методом, идентичными средствами измерений, и близость к нулю случайной погрешности измерений.
Воспроизводимость результатов измерений – близость результатов измерений одной и той же величины, полученных в разных местах, разными методами, разными средствами, разными операторами, в разное время, но приведенных к одним и тем же условиям измерений (температуре, давлению, влажности и др.).
Правильность результатов измерений определяется правильностью как самих методик измерений, так и правильностью их использования в процессе измерений, а также близостью к нулю систематической погрешности измерений.
Слайд 9Основные понятия
принцип измерений: Явление материального мира, положенное в
основу измерения.
Примеры
1 Применение эффекта Джозефсона
Основные понятия
принцип измерений: Явление материального мира, положенное в
основу измерения.
Примеры
1 Применение эффекта Джозефсона

метод измерений: Прием или совокупность приемов сравнения измеряемой величины с ее единицей или соотнесения со шкалой в соответствии с реализованным принципом измерений.
Слайд 10Основные понятия
результат (измерения величины): Множество значений величины, приписываемых измеряемой величине вместе с
Основные понятия
результат (измерения величины): Множество значений величины, приписываемых измеряемой величине вместе с

Информация, приводимая в результате измерения, определяется особенностями конкретного измерения и соответствует требованиям, предъявляемым к этому измерению. В большинстве случаев информация относится к точности измерения и выражается показателями точности, в обоснованных случаях содержит указание методики измерений. Результат измерения может быть представлен измеренным значением величины с указанием соответствующего показателя точности. К показателям точности относятся, например, среднее квадратическое отклонение, доверительные границы погрешности, стандартная неопределенность измерений, суммарная стандартная и расширенная неопределенности.
измеренное значение (величины): Значение величины, которое представляет результат измерения.
средство измерения – техническое устройство, используемое при измерениях и имеющее нормированные метрологические характеристики.
Слайд 11Основные понятия
1 Для измерения, в котором имеют место повторные показания, каждое показание
Основные понятия
1 Для измерения, в котором имеют место повторные показания, каждое показание

2 Когда диапазон истинных значений величины, представляющих измеряемую величину, мал по сравнению с неопределенностью (погрешностью) измерений, измеренное значение величины может рассматриваться как оценка, по сути дела, единственного истинного значения величины, и оно часто представляет собой среднее арифметическое или медиану отдельных измеренных значений, которые получены при повторных измерениях.
3 В случае, когда диапазон истинных значений величины, представляющих измеряемую величину, нельзя считать малым по сравнению с неопределенностью (погрешностью) измерений, измеренное значение часто будет оценкой среднего арифметического или медианы набора истинных значений величины.
4 Для понятия измеренное значение величины используют термины результат измерения и оценка значения измеряемой величины или просто оценка измеряемой величины.
Слайд 12Основные понятия
погрешность (результата измерения): Разность между измеренным значением величины и опорным значением
Основные понятия
погрешность (результата измерения): Разность между измеренным значением величины и опорным значением

Если опорное значение величины известно, как, например, при калибровке средств измерений, то известно и значение погрешности измерения. Если в качестве опорного значения выступает истинное значение величины, то значение погрешности неизвестно.
Ранее использовался термин погрешность результата измерения: отклонение результата измерения от истинного (действительного) значения измеряемой величины.
Погрешность измерения равна сумме случайной и систематической погрешностей.
Слайд 13Основные понятия
истинное значение (величины): Значение величины, которое соответствует определению измеряемой величины.
Под
Основные понятия
истинное значение (величины): Значение величины, которое соответствует определению измеряемой величины.
Под

Основные постулаты метрологии:
– истинное значение определенной величины существует и оно постоянно;
– истинное значение измеряемой величины отыскать невозможно.
Отсюда следует, что результат измерения математически связан с измеряемой величиной вероятностной зависимостью. Поскольку истинное значение есть идеальное значение, то в качестве наиболее близкого к нему используют действительное значение.
принятое значение (величины): Значение величины, по соглашению приписанное величине для данной цели.
Иногда принятое значение величины является оценкой истинного значения величины.
Неопределенность измерений, связанная с принятым значением часто достаточна мала и может быть принята равной нулю для конкретной цели. В этом случае используют понятие действительное значение величины.
действительное значение (величины): Значение величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.
Слайд 14Основные понятия
опорное значение (величины): Значение величины, которое используют в качестве основы для
Основные понятия
опорное значение (величины): Значение величины, которое используют в качестве основы для

Опорное значение величины может быть истинным значением величины, подлежащей измерению, в этом случае оно неизвестно, или принятым значением величины, в этом случае оно известно.
Опорное значение величины со связанной с ним неопределенностью (погрешностью) измерений обычно приводят для:
материала, например, аттестованного стандартного образца;
устройства, например, стабилизированного лазера;
референтной методики измерений;
сличения эталонов.
Слайд 15Основные понятия
случайная погрешность (измерения): Составляющая погрешности измерения, изменяющаяся случайным образом (по знаку
Основные понятия
случайная погрешность (измерения): Составляющая погрешности измерения, изменяющаяся случайным образом (по знаку

систематическая погрешность (измерения): Составляющая погрешности измерения, остающаяся постоянной или же закономерно изменяющаяся при повторных измерениях одной и той же величины.
В зависимости от характера изменения во времени систематические погрешности подразделяют на постоянные, прогрессирующие, периодические и погрешности, изменяющиеся по сложному закону. В зависимости от характера изменения по диапазону измерений систематические погрешности подразделяются на постоянные и пропорциональные.
Постоянные погрешности — погрешности, которые в течение длительного времени, например, в течение времени выполнения всего ряда измерений, остаются постоянными (или — неизменными). Они встречаются наиболее часто.
Прогрессирующие погрешности — непрерывно возрастающие или убывающие погрешности. К ним относятся, например, погрешности вследствие износа измерительных наконечников, контактирующих с деталью при контроле ее прибором активного контроля.
Периодические погрешности — погрешности, значение которых является периодической функцией времени или перемещения указателя измерительного прибора.
Погрешности, изменяющиеся по сложному закону, происходят вследствие совместного действия нескольких систематических погрешностей.
Пропорциональные погрешности — погрешности, значение которых пропорционально значению измеряемой величины.
Слайд 16Основные понятия
доверительные границы (погрешности измерения): Верхняя и нижняя границы интервала, внутри которого
Основные понятия
доверительные границы (погрешности измерения): Верхняя и нижняя границы интервала, внутри которого

Доверительные границы при вероятности, равной 1, называют границами погрешности. Доверительные границы погрешности иногда неправильно называют доверительная погрешность.
максимальная допускаемая погрешность (измерения): Максимальное значение погрешности измерения (без учета знака), разрешенное спецификацией или нормативными документами для данного измерения.
погрешность метода (измерений): Составляющая погрешности измерений, обусловленная несовершенством принятого метода измерений.
инструментальная погрешность (измерения): Составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений.
абсолютная погрешность (измерения): Погрешность измерения, выраженная в единицах измеряемой величины.
относительная погрешность (измерения): Погрешность измерения, выраженная отношением абсолютной погрешности измерения к опорному значению измеряемой величины.
Слайд 17Неопределенности измерений
неопределенность (измерений): Неотрицательный параметр, характеризующий рассеяние значений величины, приписываемых измеряемой
Неопределенности измерений
неопределенность (измерений): Неотрицательный параметр, характеризующий рассеяние значений величины, приписываемых измеряемой

стандартная неопределенность (измерений): Неопределенность измерений, выраженная в виде стандартного отклонения. (это по сути СКО)
суммарная стандартная неопределенность (измерений): Стандартная неопределенность измерений, которую получают суммированием отдельных стандартных неопределенностей измерений, связанных с входными величинами в модели измерений.
расширенная неопределенность (измерений): Произведение суммарной стандартной неопределенности и коэффициента охвата большего, чем 1. (это по сути доверительные границы погрешности измерений)
Коэффициент зависит от вида распределения вероятностей выходной величины в модели измерений и выбранной вероятности охвата.
оценивание (неопределенности измерений) по типу А: Оценивание составляющей неопределенности измерений путем статистического анализа измеренных значений величины, получаемых при определенных условиях измерений.
оценивание (неопределенности измерений) по типу В: Оценивание составляющей неопределенности измерений способами, отличными от оценивания неопределенности измерений по типу А. Это оценивание, основанное на информации, связанной со значениями величины, взятыми из авторитетных публикаций, связанной со значением аттестованного стандартного образца, полученной из сертификатов калибровки, о дрейфе, связанной с классом точности поверенного средства измерений или полученной исходя из пределов, установленных на основе опыта.
Слайд 18Погрешности измерения
Границы относительной погрешности в долях или процентах находят из отношений:
где
Погрешности измерения
Границы относительной погрешности в долях или процентах находят из отношений:
где

Неопределенности измерения
При классическом подходе дисперсию относят к истинному значению измеряемой величины X, в теории неопредеелнностей — к результату измерений L. Но это различие не влияет на подведение окончательных результатов, поскольку и в классическом подходе погрешности измерений также приписывают результату измерений. Таким образом, обе концепции дополняют друг друга, сливаясь в единую концепцию оценивания точности результатов измерений.
истинное значение величины => действительное значение величины => результат измерения => погрешность измерения => неопределенность результата измерения как характеристика этой погрешности.
Слайд 19Понятие о физических величинах и системах единиц
Под физической величиной понимается свойство, общее
Понятие о физических величинах и системах единиц
Под физической величиной понимается свойство, общее

Когда отдельные величины связаны между собой уравнениями, их называют системой величин. Эти уравнения между величинами установлены исследованием свойств объектов и их взаимосвязей после количественного выражения. С их помощью формулируются определения одних величин через другие, устанавливаются способы измерения.
Физические величины, единицы которых устанавливаются независимо от других величин в системе, называются основными величинами, а их единицы – основными единицами.
Слайд 20Понятие о физических величинах и системах единиц
Все остальные величины и единицы определяются
Понятие о физических величинах и системах единиц
Все остальные величины и единицы определяются

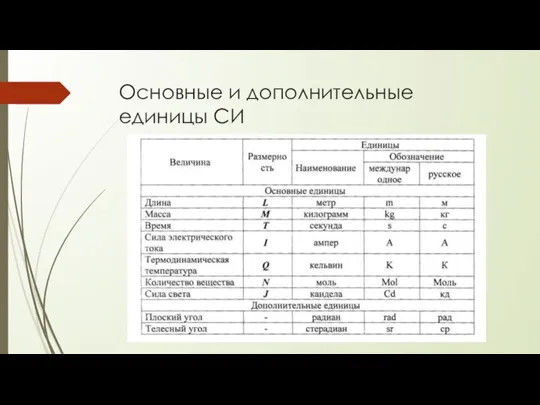
Слайд 21Основные и дополнительные единицы СИ
Основные и дополнительные единицы СИ
 Применение теоремы Пифагора
Применение теоремы Пифагора Свойства случайных погрешностей
Свойства случайных погрешностей Презентация на тему Занимательная геометрия (3 класс)
Презентация на тему Занимательная геометрия (3 класс)  Подготовка к контрольной работе
Подготовка к контрольной работе Путешествие на воздушных шарах
Путешествие на воздушных шарах Внеурочная деятельность по математике, 3 класс
Внеурочная деятельность по математике, 3 класс Сумма углов треугольника
Сумма углов треугольника деление многочлена на многочлен столбиком
деление многочлена на многочлен столбиком Канонический вид многочлена с одной переменной (урок 65)
Канонический вид многочлена с одной переменной (урок 65) Множества. Решение задач
Множества. Решение задач Уменьшаемое, вычитаемое, разность
Уменьшаемое, вычитаемое, разность Пересекающиеся и параллельные прямые
Пересекающиеся и параллельные прямые Площадь криволинейной трапеции
Площадь криволинейной трапеции Компетентностно-ориентированные задания, как средство формирования ключевых компетенций учащихся
Компетентностно-ориентированные задания, как средство формирования ключевых компетенций учащихся Презентация на тему Отношения и пропорции
Презентация на тему Отношения и пропорции  Презентация на тему Иррациональные числа (8 класс)
Презентация на тему Иррациональные числа (8 класс)  Функции и их графики. 9 класс
Функции и их графики. 9 класс Страничка для любознательных
Страничка для любознательных Решение тригонометрических уравнений
Решение тригонометрических уравнений Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Нахождение произведения по предыдущему результату. Замена умножения сложением
Нахождение произведения по предыдущему результату. Замена умножения сложением Решение планиметрических задач
Решение планиметрических задач Логарифмы
Логарифмы Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010
Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010 Задачи на проценты
Задачи на проценты Геометрия пчелиных сот
Геометрия пчелиных сот Тригонометрические функции двойного угла
Тригонометрические функции двойного угла Количественные характеристики встречаемости заболеваний
Количественные характеристики встречаемости заболеваний