Содержание
- 2. Криволинейная трапеция Отрезок [a;b] называют основанием этой криволинейной трапеции Криволинейной трапецией называется фигура, ограниченная графиком непрерывной
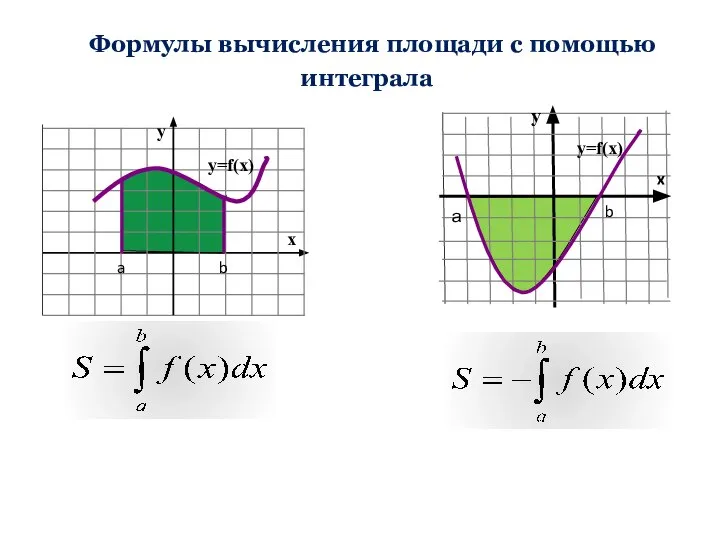
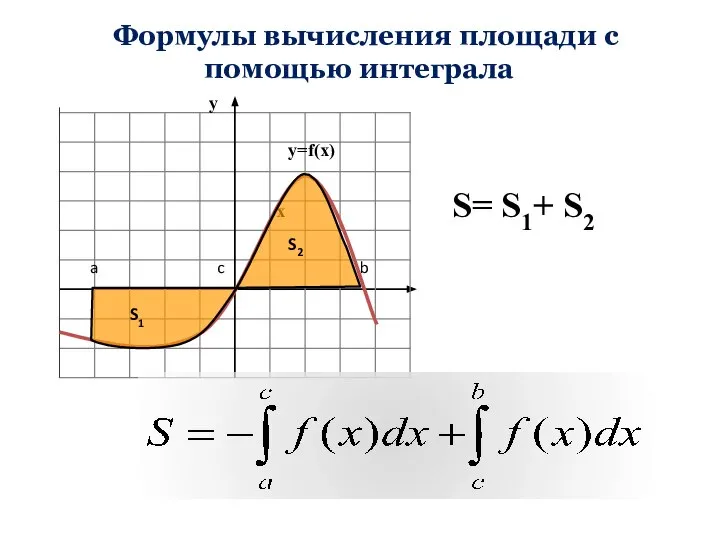
- 3. Формулы вычисления площади с помощью интеграла
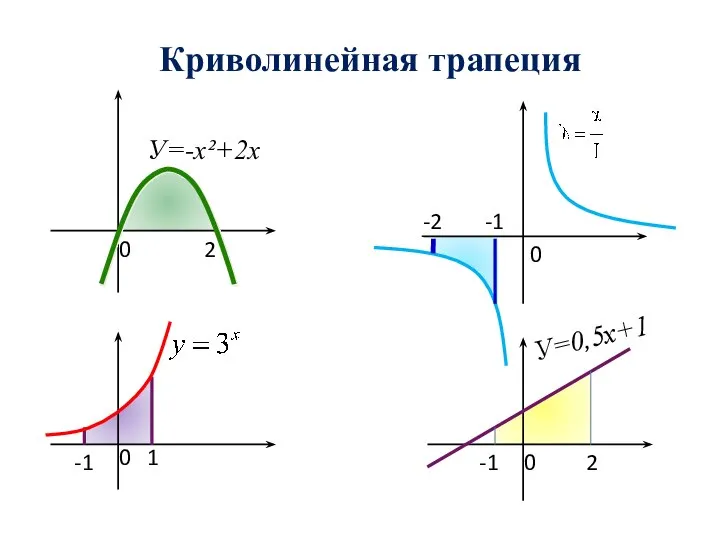
- 4. Криволинейная трапеция 0 2 0 0 0 1 -1 -1 2 -1 -2 У=-х²+2х У=0,5х+1
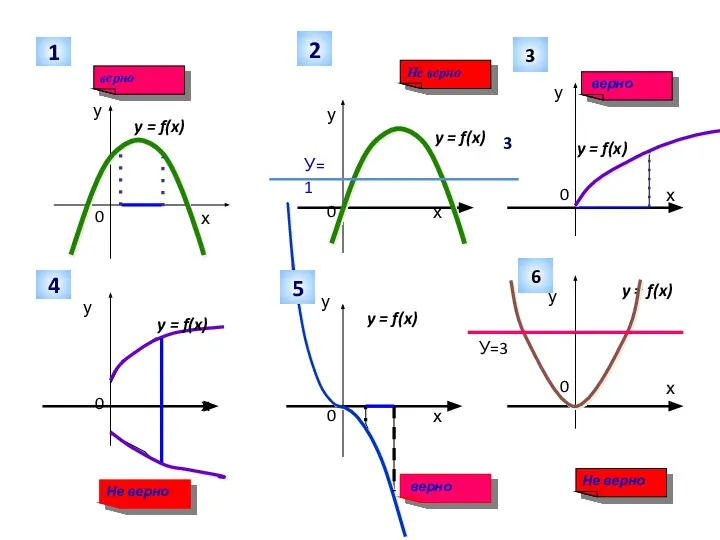
- 5. Какие из заштрихованных на рисунке фигур являются криволинейными трапециями, а какие нет? Заполнить таблицу
- 6. у 1 Не верно у у у у у У=1 2 верно 3 3 y =
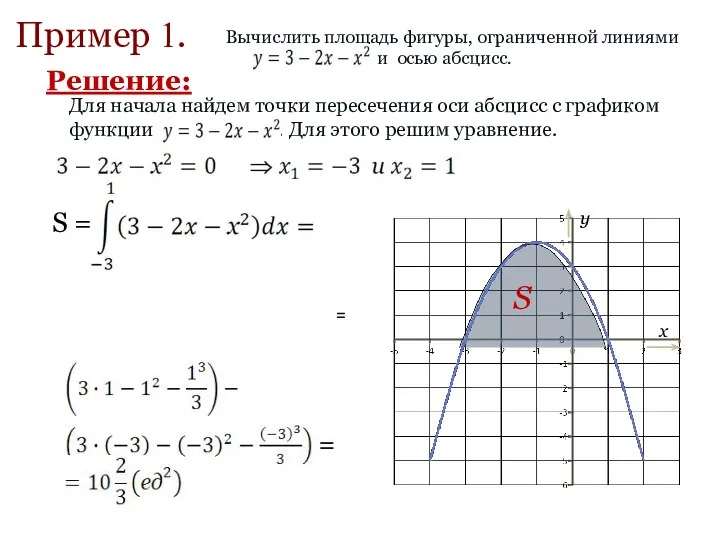
- 7. Пример 1. = Решение: S =
- 8. Формулы вычисления площади с помощью интеграла х S= S1+ S2
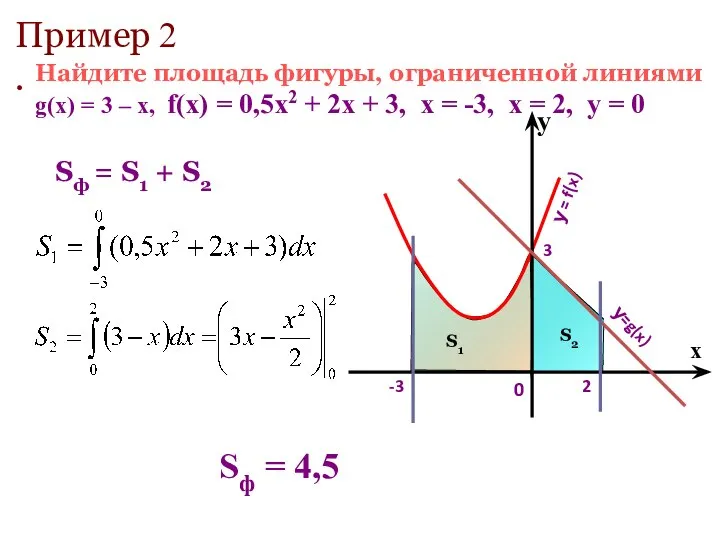
- 9. Найдите площадь фигуры, ограниченной линиями g(x) = 3 – х, f(x) = 0,5х2 + 2х +
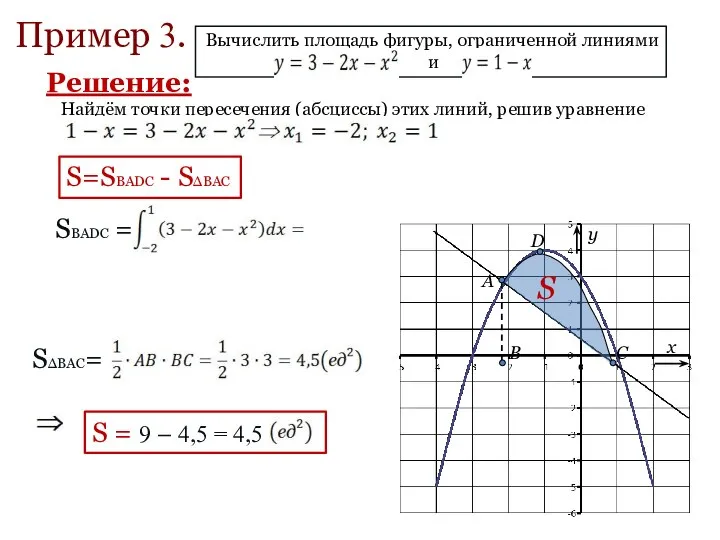
- 10. Пример 3. Найдём точки пересечения (абсциссы) этих линий, решив уравнение S=SBADC - SΔBAC SBADC = SΔBAC=
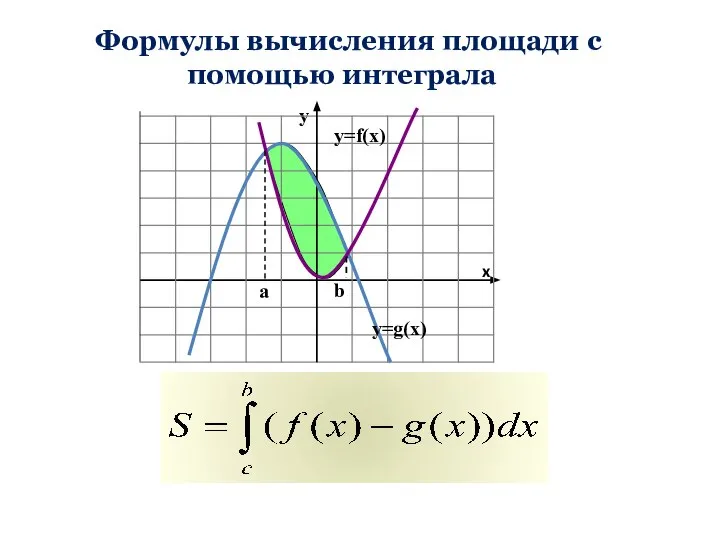
- 11. Формулы вычисления площади с помощью интеграла x
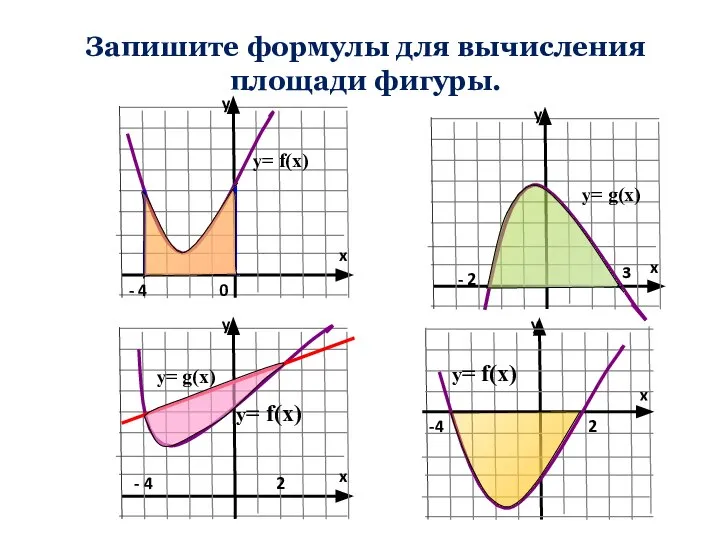
- 12. y Запишите формулы для вычисления площади фигуры. y= f(x) y= f(x) -4 2 - 2 3
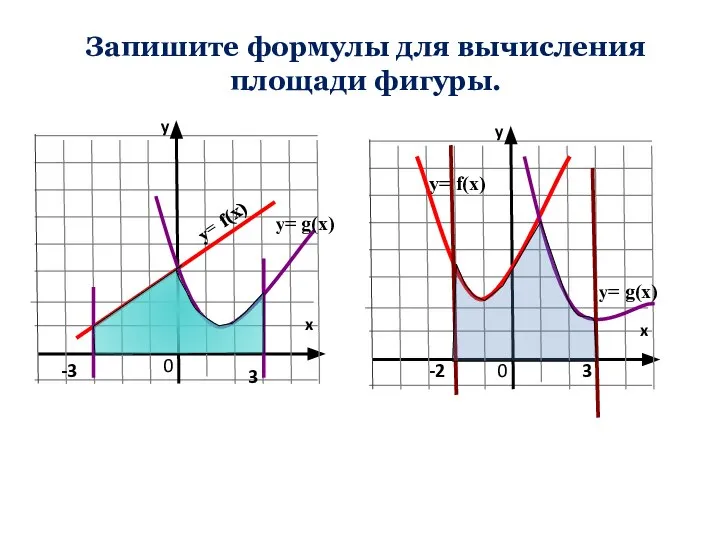
- 13. y= f(x) y= f(x) y= g(x) -3 3 0 Запишите формулы для вычисления площади фигуры. y=
- 15. Скачать презентацию
![Криволинейная трапеция Отрезок [a;b] называют основанием этой криволинейной трапеции Криволинейной трапецией называется](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/948928/slide-1.jpg)

 Цепочка бусин
Цепочка бусин Аксиомы и теоремы
Аксиомы и теоремы Решение уравнений. Устная работа
Решение уравнений. Устная работа ОДУ высших порядков
ОДУ высших порядков Экстремум функции нескольких переменных. Наибольшее и наименьшее значение функции в замкнутой ограниченной области (тема 1.4)
Экстремум функции нескольких переменных. Наибольшее и наименьшее значение функции в замкнутой ограниченной области (тема 1.4) Презентация на тему Решение неравенств второй степени с одной переменной
Презентация на тему Решение неравенств второй степени с одной переменной  Прогрессии. Основные формулы арифметической прогрессии
Прогрессии. Основные формулы арифметической прогрессии Презентация на тему Цифра 5, число 5, состав числа 5
Презентация на тему Цифра 5, число 5, состав числа 5  Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 1
Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 1 Вставляем пропущенное число с дракончиками. Урок математики
Вставляем пропущенное число с дракончиками. Урок математики Задачи на построение
Задачи на построение Аттестационная работа. Доли. Обыкновенные дроби. (5 класс)
Аттестационная работа. Доли. Обыкновенные дроби. (5 класс) Следствия из теорем синусов и косинусов
Следствия из теорем синусов и косинусов Примеры на состав числа 6
Примеры на состав числа 6 Найдите лишнюю фигуру и объясните свой выбор
Найдите лишнюю фигуру и объясните свой выбор Объем тела. Объем призмы, пирамиды, усечённой пирамиды
Объем тела. Объем призмы, пирамиды, усечённой пирамиды Математическая игра «Звездный час»
Математическая игра «Звездный час» Множення і ділення
Множення і ділення Диференціальне числення функції однієї змінної
Диференціальне числення функції однієї змінної Декартова система координат в пространстве
Декартова система координат в пространстве П 3
П 3 Математическая тревожность
Математическая тревожность Презентация на тему Транспортир. Измерение углов транспортиром
Презентация на тему Транспортир. Измерение углов транспортиром  Линейная алгебра. Матрицы
Линейная алгебра. Матрицы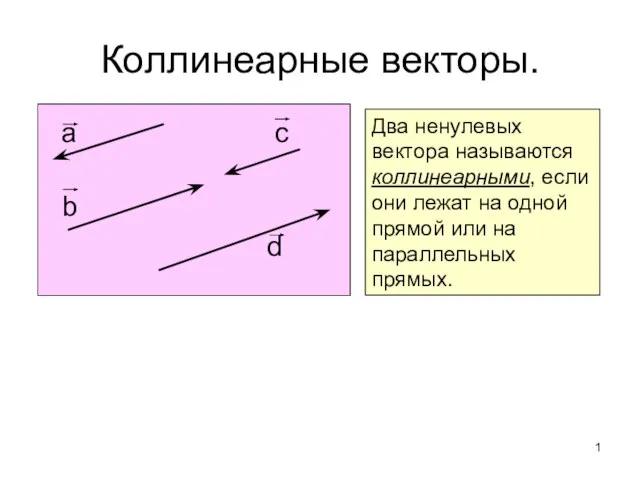 Коллинеарные векторы
Коллинеарные векторы Задачи на количество
Задачи на количество Урок 14. Первый признак равенства треугольников
Урок 14. Первый признак равенства треугольников Таблица умножения в пределах 100. Урок повторения и закрепления
Таблица умножения в пределах 100. Урок повторения и закрепления