Свойства случайных погрешностей

Вероятнейшие ошибки

Средняя квадратичная ошибка отдельного измерения

Кривая Гаусса

Кривая Гаусса
с1>с
Для с1 кривая получается более узкая, чем для c. Такой ряд

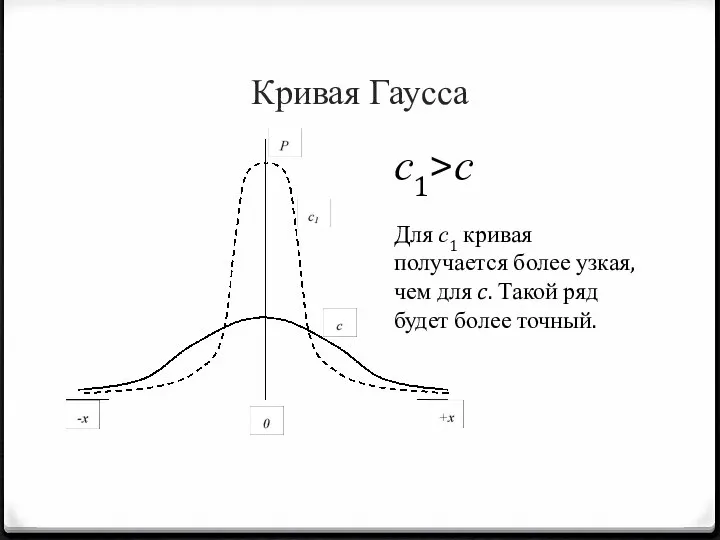
будет более точный.

Кривая Гаусса

Средняя среднеквадратичная ошибка окончательного результата измерений

Предельная случайная ошибка
Предельной случайной ошибкой xпр называют самую большую из всех случайных

ошибок в данном ряду равноточных измерений.
Случайные ошибки распределяются по отношению к средней квадратичной ошибке отдельного измерения следующим образом:
68,3 % случайных ошибок меньше Sn;
95,7 % этих ошибок меньше 2Sn;
99,7 % − меньше 3Sn.
Таким образом, принимают, что для всякого рода равноточных измерений предельная случайная ошибка с вероятностью, близкой к 100 %, равна 3Sn

Слайд 12

Предельная случайная ошибка

Слайд 13

Доверительный интервал
Предыдущая запись справедлива при достаточно большом числе измерений.
В 1908 году

Уильям Сили Госсет (псевдоним Стьюдент), применил статистический подход при определении ошибок для небольшого числа измерений (менее 30). При этом в случае n → ∞, распределение Стьюдента переходит в распределение Гаусса.
Если существует величина α вероятности отличия результата измерений от истинного значения на величину не более, чем Δaсл, она называется доверительной вероятностью, а интервал значений oт X−Δaсл до X+Δaсл называется доверительным интервалом.

Слайд 14

Доверительный интервал

Слайд 15

Практическое занятие №1
Задание 2.
Найти среднюю квадратичную ошибку отдельного измерения Sn и

среднюю среднеквадратичную ошибку S результатов 50-ти измерений маятника №1 по зависимостям

Слайд 16

Практическое занятие №1

Слайд 17

Практическое занятие №1

Слайд 18

Практическое занятие №1
Задание 2.
Повторить вычисления пунктов 1-3 для маятников №3, №4.

Для маятника №2 взять среднеквадратичную ошибку Sn и значение tα,n из результатов для маятника №1, так как эксперимент проводится в одних и тех же условиях, одним и тем же экспериментатором.
Записать результаты измерений для всех маятников и сделать выводы. При этом учитывать число верных знаков в результатах измерений.