Содержание
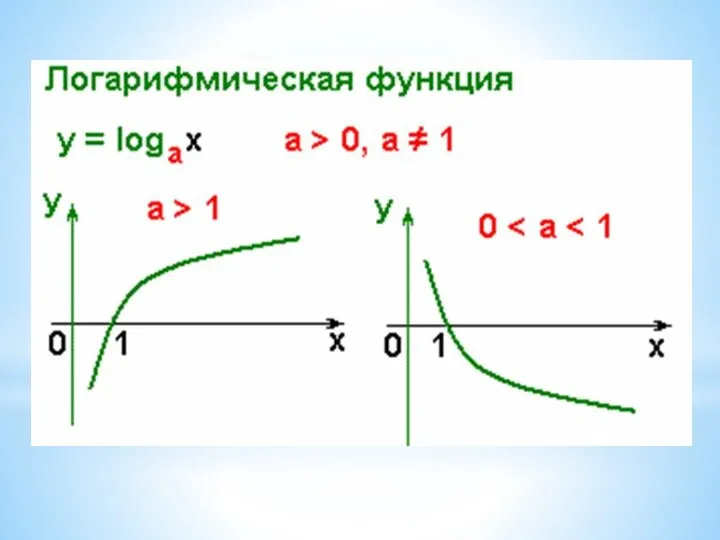
- 2. Логарифмом числа b по основанию a ( b > 0, a > 0, a=1 ) называют
- 3. Основное логарифмическое тождество: Из определения логарифма получаются следующие важные равенства: loga1=0 logaa=1 Эти тождества следуют из
- 5. Свойства логарифмов
- 6. Логарифм по основанию e имеет в математике большое значение. Число e приблизительно равно 2,71, однако само
- 7. История Принцип, лежащий в основе любой системы логарифмов, известен очень давно и может быть прослежен в
- 8. Логарифм. Название введено Непером, происходит от греческих слов logoz и ariumoz - оно означает буквально “числа
- 9. В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов
- 11. Скачать презентацию







 Геометрия в живописи
Геометрия в живописи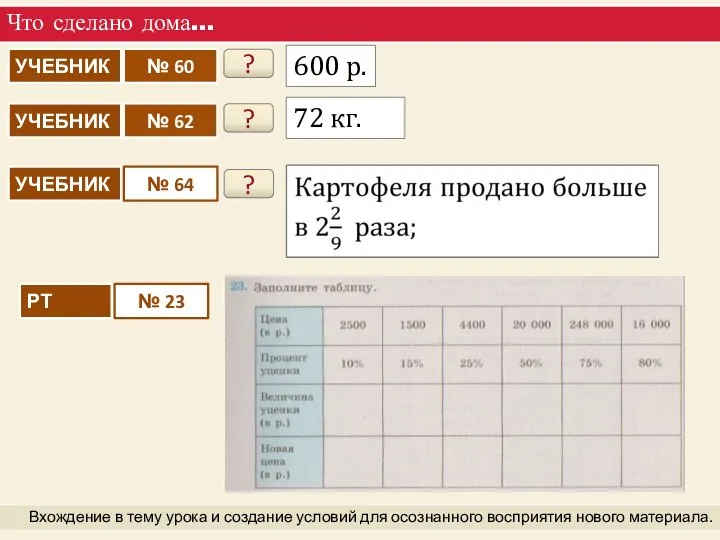 Решение задач на проценты
Решение задач на проценты Презентация на тему Статистика и математика
Презентация на тему Статистика и математика  Геометрические преобразования пространства
Геометрические преобразования пространства Задачи для всех-всех-всех
Задачи для всех-всех-всех Надежность производственных и технологических систем. Математические модели в теории надежности
Надежность производственных и технологических систем. Математические модели в теории надежности Пирамида и её элементы. Правильная пирамида
Пирамида и её элементы. Правильная пирамида Типовые звенья
Типовые звенья Признак параллельности плоскостей
Признак параллельности плоскостей Сложение и вычитание числа 2
Сложение и вычитание числа 2 Арифметический квадратный корень. Классная работа
Арифметический квадратный корень. Классная работа Подготовка к контрольной работе №1
Подготовка к контрольной работе №1 Закрепление. Повтори правила стр. 72, 74
Закрепление. Повтори правила стр. 72, 74 Презентация на тему Синус, косинус, тангенс острого угла прямоугольного треугольника
Презентация на тему Синус, косинус, тангенс острого угла прямоугольного треугольника  Понятие десятичной дроби. Разряды десятичных дробей
Понятие десятичной дроби. Разряды десятичных дробей Презентация на тему Сумма углов треугольника
Презентация на тему Сумма углов треугольника  Решение задач по теме: Элементы алгебры логики
Решение задач по теме: Элементы алгебры логики Показательные неравенства 11 класс
Показательные неравенства 11 класс Логарифмические неравенства. Решение заданий
Логарифмические неравенства. Решение заданий Векторы на плоскости и в пространстве
Векторы на плоскости и в пространстве Вариант 1
Вариант 1 Письменное умножение чисел, оканчивающихся нулями
Письменное умножение чисел, оканчивающихся нулями Показательные уравнения и неравенства
Показательные уравнения и неравенства Тест по алгебре Для учащихся 11 класса по теме «Производная» Тест состоит из пяти вопросов.
Тест по алгебре Для учащихся 11 класса по теме «Производная» Тест состоит из пяти вопросов. Смежные углы
Смежные углы Элементы комбинаторики
Элементы комбинаторики preobrazovanie
preobrazovanie Принадлежность точки выделенной области. 10 класс
Принадлежность точки выделенной области. 10 класс