Лекция 5_1_СЛАУ_Итерац методы

Сходимость и скорость сходимости последовательности к точному решению зависят от выбора нач. приближения и свойств матрицы А.
Итерация – это переход от одного приближенного реш. к другому: х(к)→х(к+1), где к – номер итер., к=1,2,…
Метод сходится, если построенная послед-ть значений стремится в пределе к точному значению:
х(к) → х*, к=1,2,…
где х* - точное решение (оно неизвестно).
На практике процесс вычислений останавливают, если выполняется условие остановки:
||x(k) – x(k+1)||≤ε ,
где ε>0 – достаточно малое число (параметр метода, выбирается заранее, например, ε=10-4).

Если условие остановки выполняется, то х*=х (к+1) принимают за решение задачи с точностью ε.
Для справки: Норма вектора может быть вычислена по-разному. Например,
1. ||z|| = – евклидова норма.
Тогда условие остановки принимает вид:
2.

2. Метод простой итерации
СЛАУ: Ax=b
Нужно привести к виду: x=G x + g
Итерационная формула метода простой итерации:
x(k+1) = G x(k) +g, k=0,1,2,… ,
Метод простой итерации сходится не всегда.
Известно, что метод сходится для любого начального приближения х(0) со скоростью геометрической прогрессии, если норма матрицы G меньше единицы.
Например, =
– максимальная из сумм модулей элементов в столбце (или в строке).

Достаточное условие сходимости к решению системы: матрица A должна иметь диагональное преобладание
В качестве начального вектора x(0) рекомендуется брать вектор g.

Алгоритм метода простых итераций
1. Преобразовать систему Ax=b к виду x=G x + g.
2. Задать начальное приближение решения х(0) произвольно или положить х(0) =g , задать малое положительное число ε (точность приближения). Положить k=0.
3. Вычислить следующее приближение
x(k+1) = G x(k) +g
4. Проверить условие остановки:
если ||x(k) – x(k+1)||≤ε , то процесс завершить и в качестве приближенного решения задачи принять х*= х(к+1) .
Иначе положить k = k + 1 и перейти к пункту 3 алгоритма.

Пример 1.
Методом простых итераций с точностью решить систему линейных алгебраических уравнений:

Решение. 1. Так как
, то ни одно уравнение системы не имеет диагонального преобладания. Переставим уравнения:
Исх. СЛАУ:

Выразим из первого уравнения x1, из второго х2, из третьего х3 :
Так как (в стр.), то метод будет сходиться для любого нач. приближения.
G=
g=
‖G‖= max
x=G x + g

2. Зададим
Пусть
3. Выполним расчеты по итерац. формуле :
до выполнения условия остановки.
g=

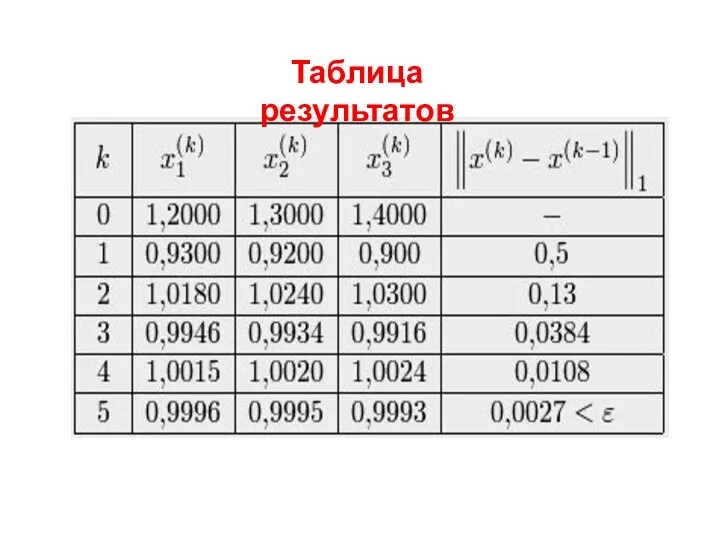
Таблица результатов

4. Расчет закончен, поскольку выполнено условие окончания
Приближенное решение задачи:
Очевидно, точное решение:
Приведем результаты расчетов для другого начального приближения и

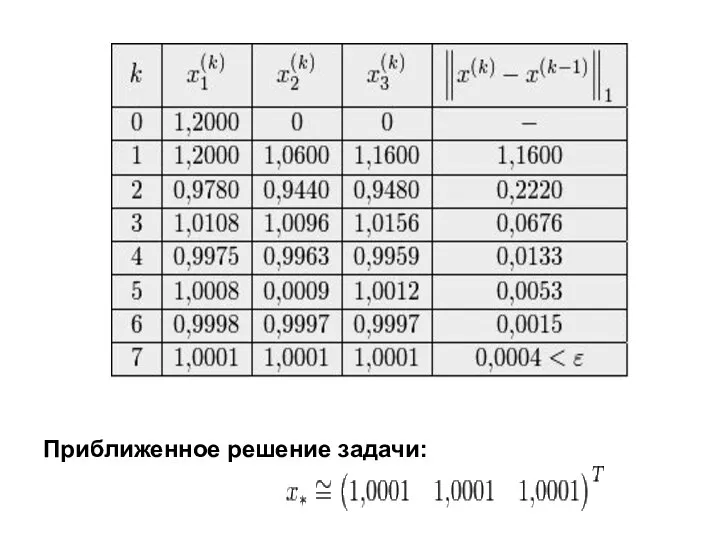
Приближенное решение задачи:

2. Метод Зейделя
Итерационный процесс задается формулой:
х(k+1) = P x(k+1) + Q x(k) + g, k=0,1,2,…
Матрицы P и Q строятся по матрице G:
Метод Зейделя – частный случай метода простой итерации (см. материал)

Метод Зейделя начинает работу с любого начального приближения. Условия сходимости метода те же, что и для метода простой итерации, но проверять их нужно для матрицы

Метод простой
итерации
Метод Зейделя
Расчетные формулы методов в покомпонентной записи (общий случай, нелинейный)

Если для некоторой СЛАУ сходятся оба метода, то известно, что предпочтительнее метод Зейделя. Можно привести примеры, когда один метод сходится к точному решению, а другой – нет (методы имеют разные области сходимости).
Если выполняется достаточное условие сходимости для метода простой итерации по строкам, то в методе Зейделя выгодно расположить уравнения в порядке возрастания суммы модулей коэффициентов.