Содержание
- 2. 3.1. ЛОГИЧЕСКИЕ ОПЕРАЦИИ Переменная x называется логической, если x ∈ {0, 1}. Над логическими переменными определены
- 3. Базовые операции над логическими переменными: 1. Отрицание Обозначается: Таблица истинности логической операции «отрицание»: Отрицание соответствует союзу
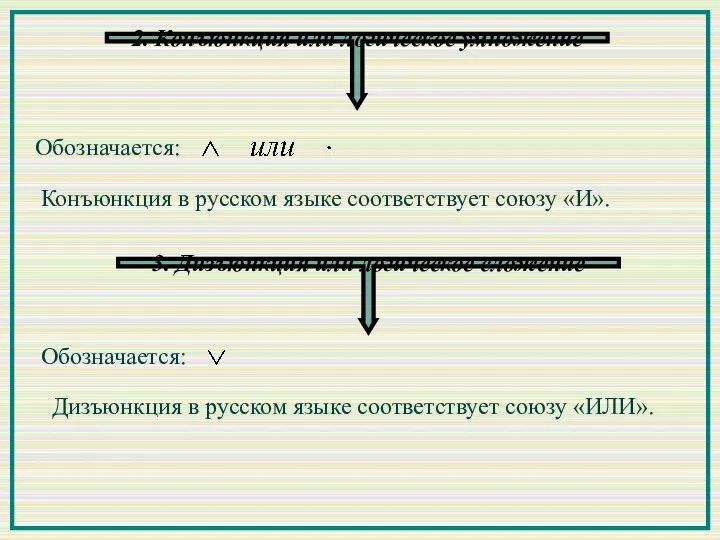
- 4. 2. Конъюнкция или логическое умножение Обозначается: Конъюнкция в русском языке соответствует союзу «И». 3. Дизъюнкция или
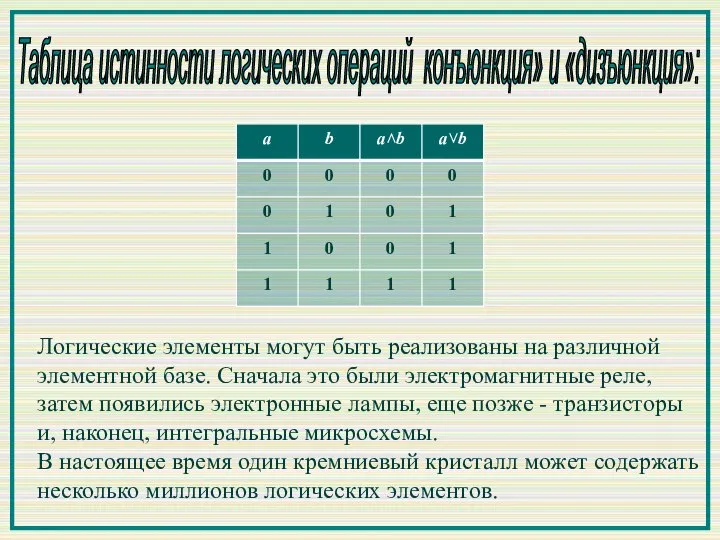
- 5. Таблица истинности логических операций конъюнкция» и «дизъюнкция»: Логические элементы могут быть реализованы на различной элементной базе.
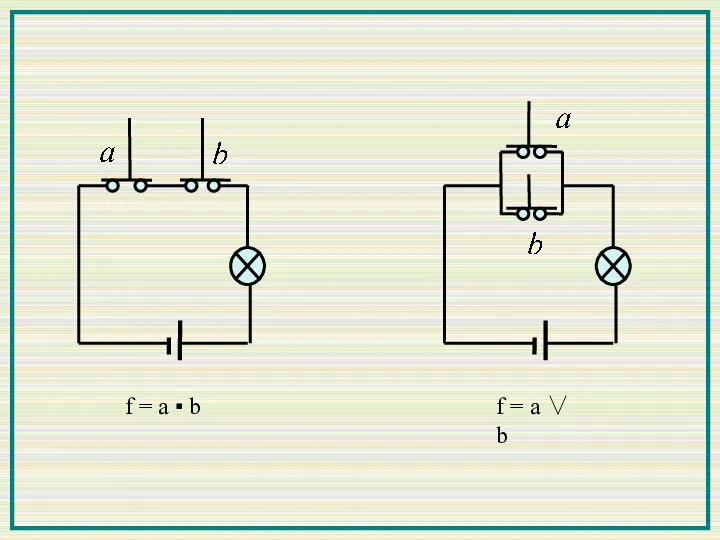
- 6. Рассмотрим реализацию логики на электромагнитных релейно-контактных схемах. Если логическая переменная a = 1, то реле замкнуто,
- 7. f = a ∨ b f = a ▪ b
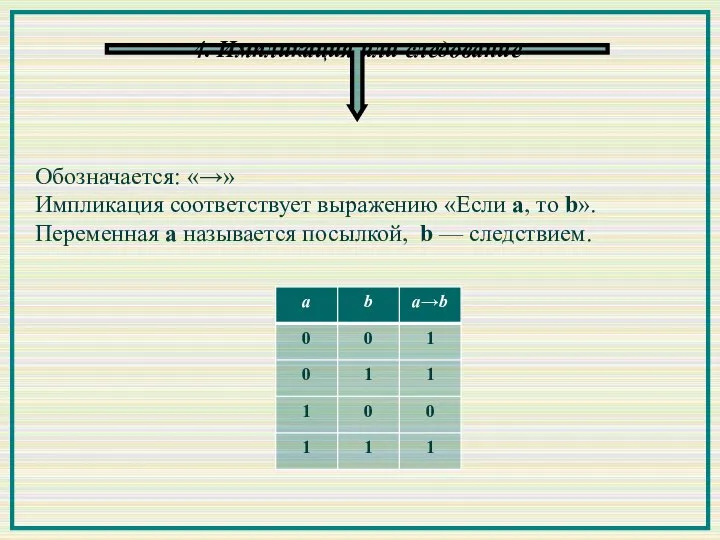
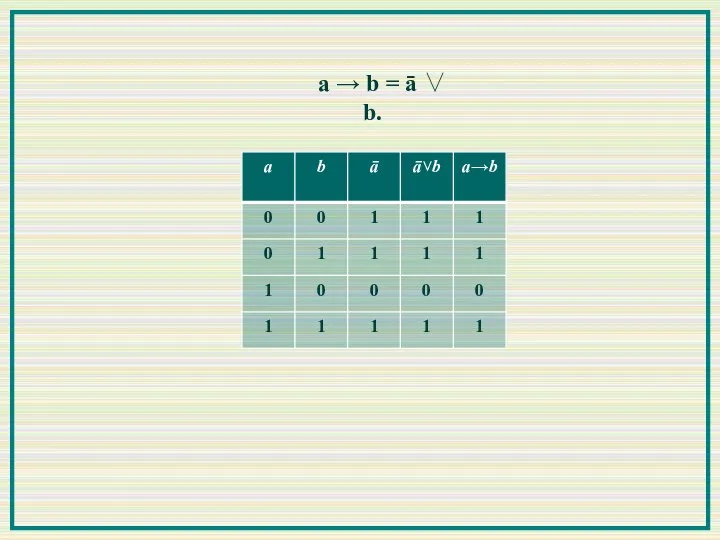
- 8. 4. Импликация или следование Обозначается: «→» Импликация соответствует выражению «Если а, то b». Переменная a называется
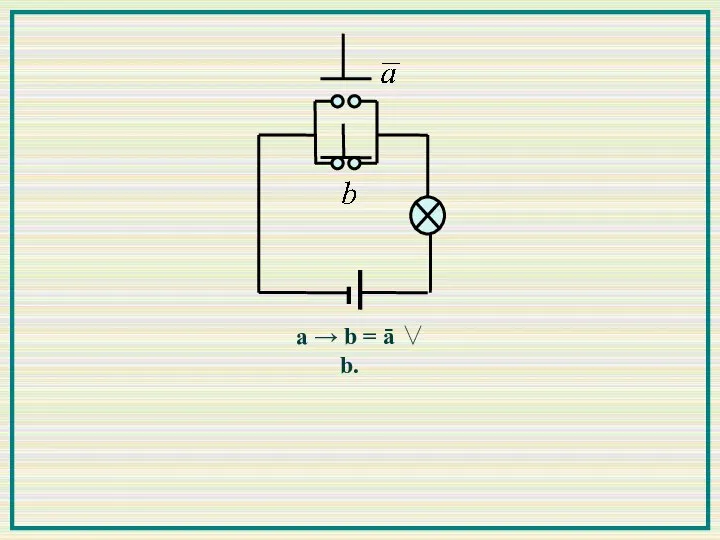
- 9. а → b = ā ∨ b.
- 10. а → b = ā ∨ b.
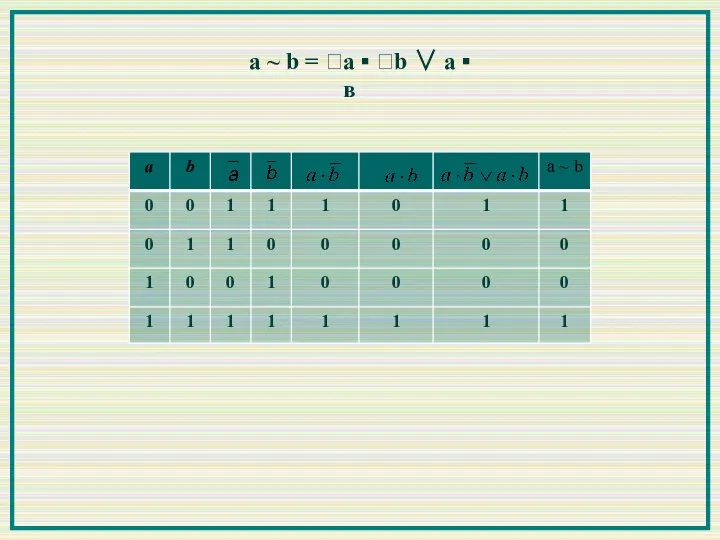
- 11. 5. Эквиваленция или равнозначность Обозначается: а ~ b Эквиваленция соответствует выражению «a, если и только если
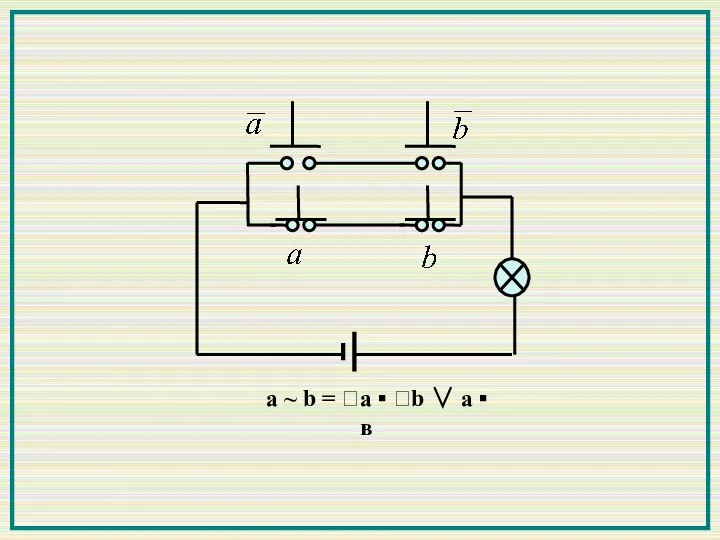
- 12. а ~ b = a ▪ b ∨ а ▪ в
- 13. а ~ b = a ▪ b ∨ а ▪ в
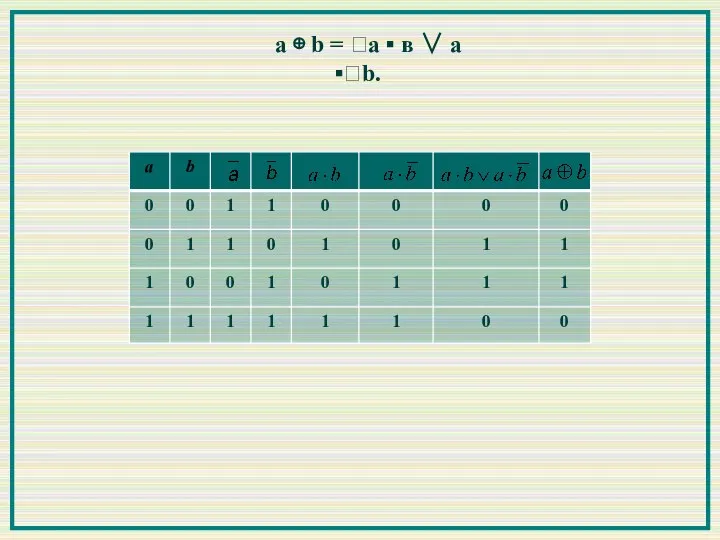
- 14. 5. Неравнозначность Обозначается: a ⊕ b Неравнозначность противоположна эквиваленции и соответствует выражению «либо a, либо b».
- 15. Другое название неравнозначности — «исключающее ИЛИ». Оно говорит о том, что на наборах «1, 1» и
- 16. a ⊕ b = a ▪ в ∨ a ▪b.
- 18. Скачать презентацию






 Разность и её значение
Разность и её значение Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости Числительные. Количественные числительные
Числительные. Количественные числительные Оценочная и сравнительная классификация алгоритмов
Оценочная и сравнительная классификация алгоритмов Движение в пространстве
Движение в пространстве Эйлеровы графы. Лекция 08
Эйлеровы графы. Лекция 08 Перпендикулярные прямые в пространстве
Перпендикулярные прямые в пространстве Решение квадратных уравнений с параметрами. Метод плавающей параболы
Решение квадратных уравнений с параметрами. Метод плавающей параболы Понятие неравенство
Понятие неравенство Степень с отрицательным показателем
Степень с отрицательным показателем Математическая логика
Математическая логика Презентация на тему Простейшие задачи в координатах (9 класс)
Презентация на тему Простейшие задачи в координатах (9 класс)  Построение 3 видов группы геометрических тел
Построение 3 видов группы геометрических тел Занимательные головоломки
Занимательные головоломки Сложение однозначных чисел с переходом через десяток вида * + 6
Сложение однозначных чисел с переходом через десяток вида * + 6 Правила комбинаторики. Практическое занятие
Правила комбинаторики. Практическое занятие Случаи вычитания 18 -
Случаи вычитания 18 - Сумма углов в треугольнике
Сумма углов в треугольнике Функции у=|x| и ей график
Функции у=|x| и ей график Косвенные измерения
Косвенные измерения Azərbaycan Dövlət Neft və Sənaye Universiteti Optimal Control
Azərbaycan Dövlət Neft və Sənaye Universiteti Optimal Control Решение задач геометрия
Решение задач геометрия Координаты
Координаты Графики функции
Графики функции Раскрытие скобок
Раскрытие скобок Первый признак равенства треугольников
Первый признак равенства треугольников Презентация на тему Прибавление числа 5 (1 класс)
Презентация на тему Прибавление числа 5 (1 класс)  Золотое сечение и симметрия
Золотое сечение и симметрия