Содержание
- 2. Суммой векторов (а;b;с) и (m;n;k) называется вектор (a+m;b+n;c+k) Например, найти координаты вектора , если (-5;3;-9) и
- 3. Произведением вектора (а;в;с) на число λ называется вектор λ (λа; λв; λс) Например, найти координаты вектора
- 4. Скалярным произведением векторов (а;в;с) и (х;у;z) называется число =ax+вy+cz Например, найти скалярное произведение векторов и Решение:
- 6. Скачать презентацию



 Вуншарлă ваксене тулли хисеп çине хутлассине аса илесси. 5 klass
Вуншарлă ваксене тулли хисеп çине хутлассине аса илесси. 5 klass Презентация на тему ПРИМЕНЕНИЕ РАЗЛИЧНЫХ СПОСОБОВ РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ МНОГОЧЛЕНА
Презентация на тему ПРИМЕНЕНИЕ РАЗЛИЧНЫХ СПОСОБОВ РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ МНОГОЧЛЕНА  Презентация на тему Степень с рациональным показателем (9 класс)
Презентация на тему Степень с рациональным показателем (9 класс)  Игра по станциям математический турнир. 7 класс
Игра по станциям математический турнир. 7 класс Решение задач на движение
Решение задач на движение Многочлены от одной переменной. Лекция 1
Многочлены от одной переменной. Лекция 1 Область определения функции. С/Р
Область определения функции. С/Р Угол
Угол Интерполяция функций
Интерполяция функций Сложение смешанных дробей
Сложение смешанных дробей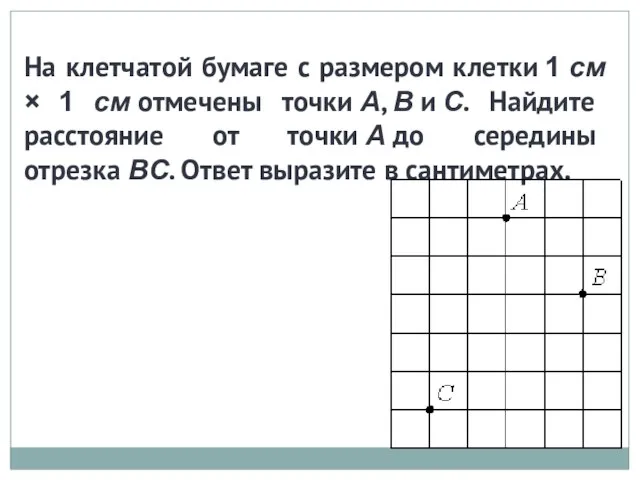 Решение задач
Решение задач Усвоение соответствий понятий о свойствах функции и её производной. Открытый банк заданий ЕГЭ
Усвоение соответствий понятий о свойствах функции и её производной. Открытый банк заданий ЕГЭ Весёлые задачки
Весёлые задачки Конус
Конус Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Násobíme a delíme s Mimoňmi
Násobíme a delíme s Mimoňmi Эконометрическое моделирование
Эконометрическое моделирование Векторы. Свойства равных векторов
Векторы. Свойства равных векторов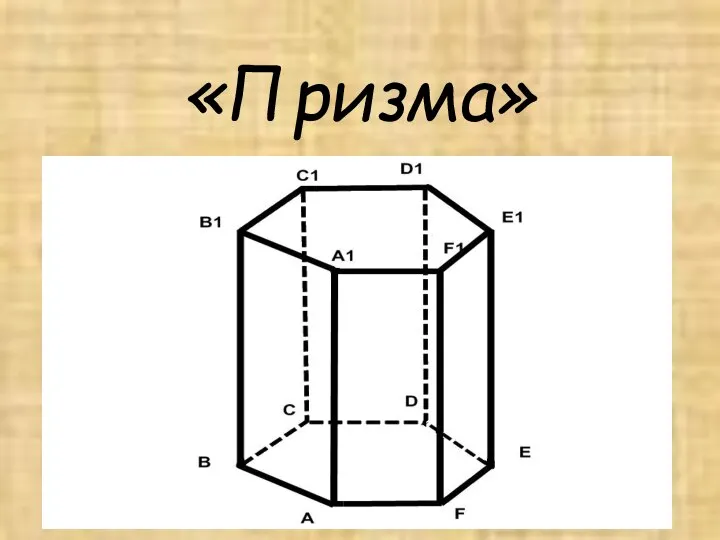 Призма. Определение призмы
Призма. Определение призмы Полные, неполные и приведенные квадратные уравнения
Полные, неполные и приведенные квадратные уравнения Решение задачи №1 заочного этапа
Решение задачи №1 заочного этапа Вектор Вектор – отрезок, для которого указано, какой из его концов считается началом, а какой – концом.
Вектор Вектор – отрезок, для которого указано, какой из его концов считается началом, а какой – концом. Простейшие задачи. Теоретический тест в координатах
Простейшие задачи. Теоретический тест в координатах Смежные и вертикальные углы
Смежные и вертикальные углы Презентация на тему Производная функции
Презентация на тему Производная функции  Принцип математической индукции (аксиома алгебры)
Принцип математической индукции (аксиома алгебры) Задача № 106
Задача № 106 بخش دوم :حل معادله درجه 2و کاربرد آن ریاضی دهم آنسانی
بخش دوم :حل معادله درجه 2و کاربرد آن ریاضی دهم آنسانی