Содержание
- 2. п.1. Окружность. Окружность есть геометрическое множество точек на плоскости, Окружность есть геометрическое множество точек на плоскости,
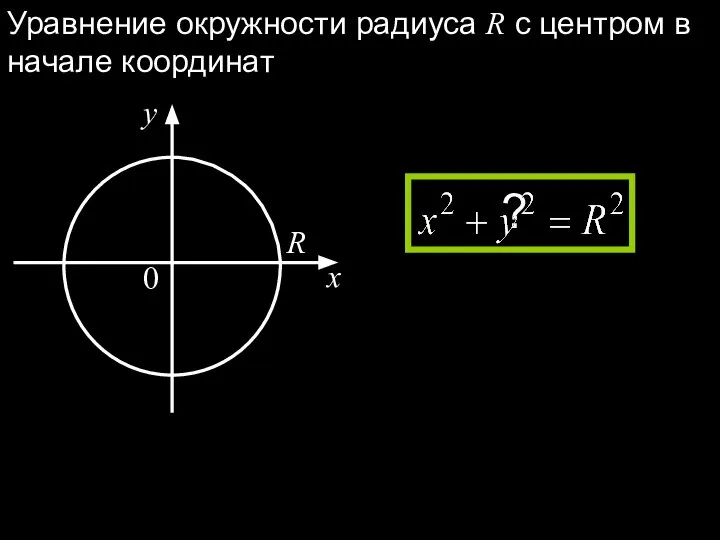
- 3. Уравнение окружности радиуса R с центром в начале координат ?
- 4. Уравнение окружности радиуса R с центром в точке ?
- 5. п.2. Эллипс. Эллипс есть геометрическое место точек на плоскости, координаты которых удовлетворяют уравнению
- 6. Свойства эллипса 1.Симметрия относительно осей координат и начала координат. 2. 3. I-я четверть: x y a
- 7. Вершины эллипса: Центр эллипса: Большая ось : Малая ось : Большая полуось : Малая полуось :
- 8. Теорема 1. Точка M плоскости принадлежит эллипсу тогда и только тогда, Теорема 1. Точка M плоскости
- 9. x y O
- 10. Доказательство. Необходимость. Пусть точка лежит на эллипсе. Покажем, что
- 13. Самостоятельно
- 14. Достаточность. Пусть Покажем, что точка лежит на эллипсе.
- 16. Теорема доказана.
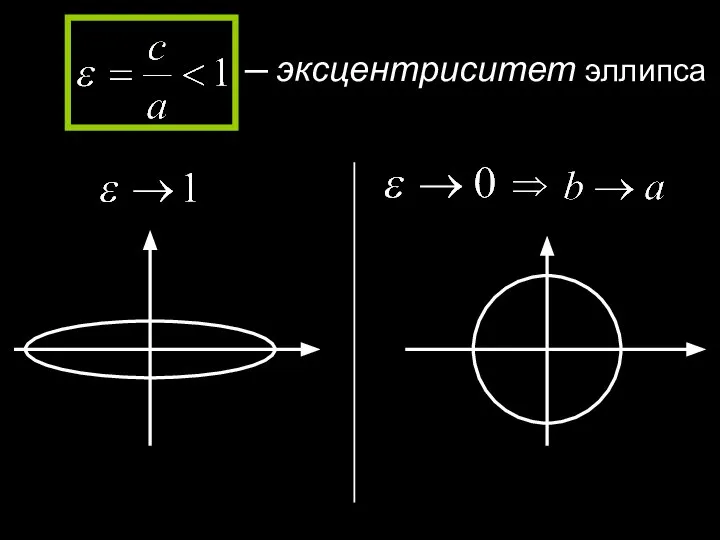
- 17. ─ эксцентриситет эллипса
- 18. Уравнение эллипса с центром в точке O
- 20. п.3. Гипербола. Гипербола есть геометрическое место точек, координаты которых удовлетворяют уравнению
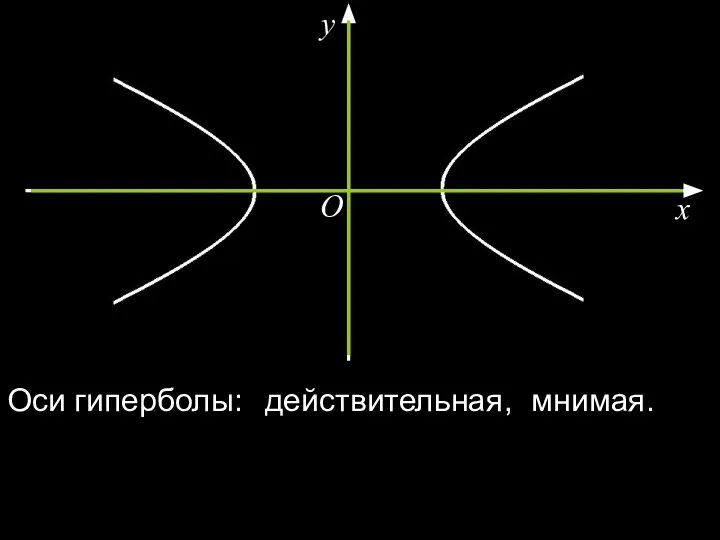
- 21. x y O Оси гиперболы: действительная, мнимая.
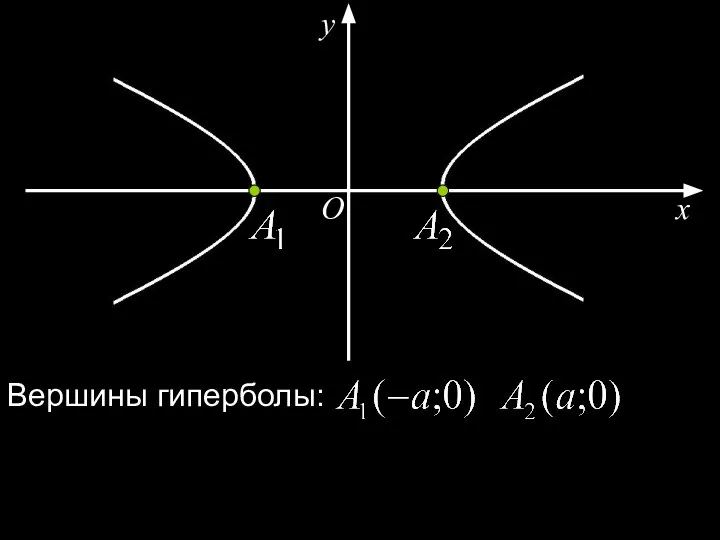
- 22. x y O Вершины гиперболы:
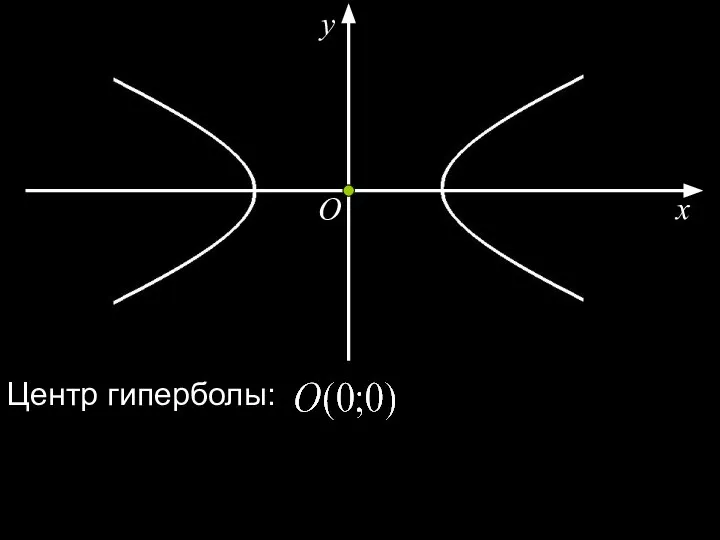
- 23. x y O Центр гиперболы:
- 24. x y O Фокусы гиперболы:
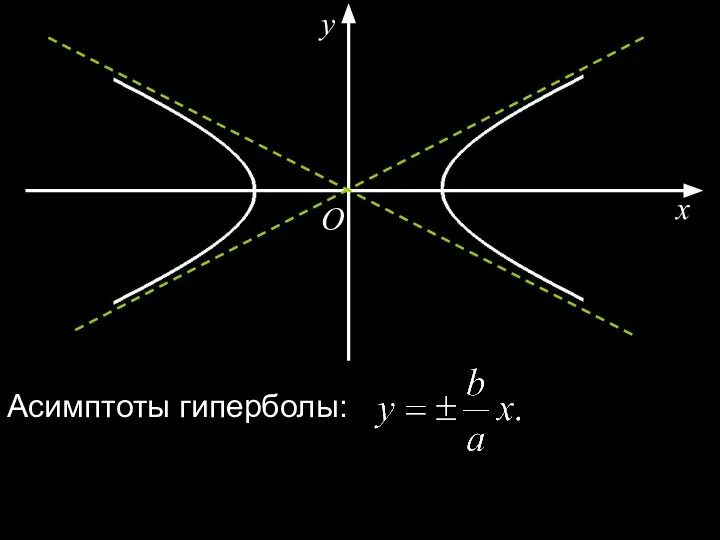
- 25. x y O Асимптоты гиперболы:
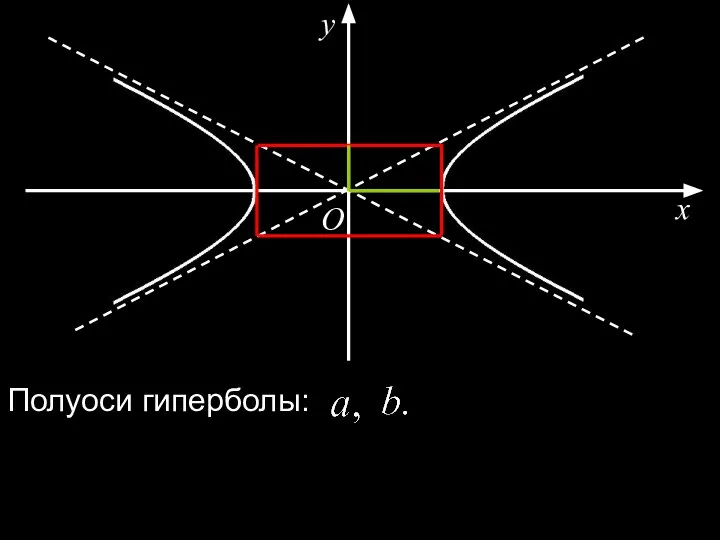
- 26. x y O Полуоси гиперболы:
- 27. Теорема 2. Точка M плоскости принадлежит гиперболе тогда и только тогда, Теорема 2. Точка M плоскости
- 28. Свойства гиперболы 1. Симметрия относительно осей координат и начала координат. 2. Не пересекает ось Oy. 3.
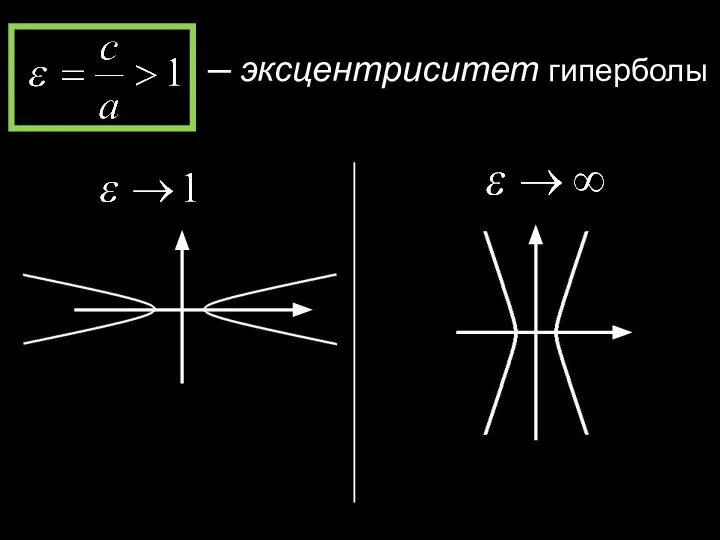
- 29. ─ эксцентриситет гиперболы
- 30. Уравнение гиперболы с центром в точке O
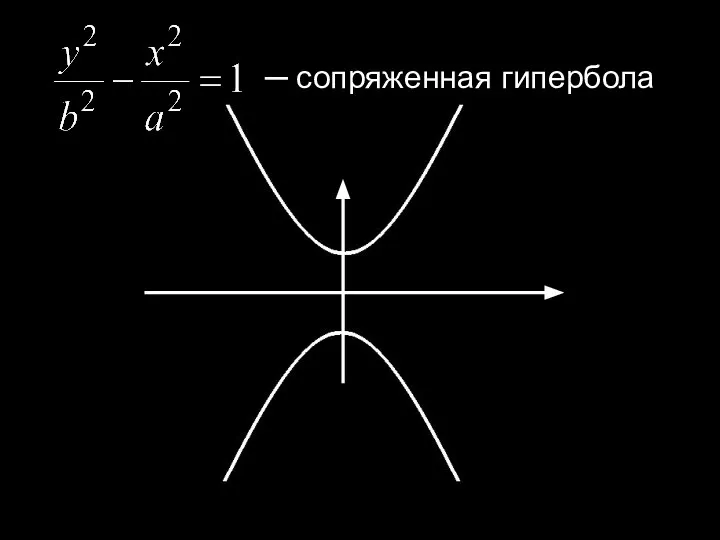
- 31. ─ сопряженная гипербола
- 32. п.4. Парабола. Парабола есть геометрическое место точек, координаты которых удовлетворяют уравнению
- 33. Ось параболы: Ось параболы: Ox. Вершина параболы: Фокус: Директриса: Расстояние от фокуса до директрисы:
- 34. Теорема 3. Точка M плоскости принадлежит параболе тогда и только тогда, Теорема 3. Точка M плоскости
- 35. Доказательство самостоятельно. x y O
- 36. Свойства параболы 1. Симметрия относительно оси Ox. 2. 3. Проходит через начало координат.
- 37. Уравнение параболы с центром в точке
- 39. Скачать презентацию






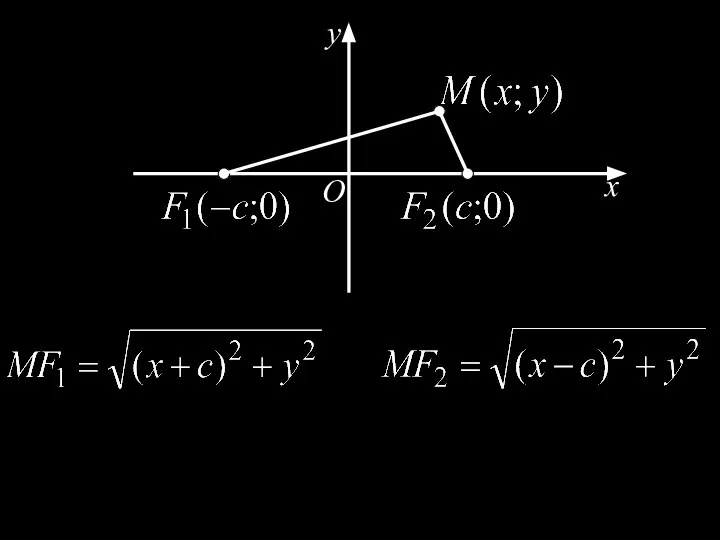


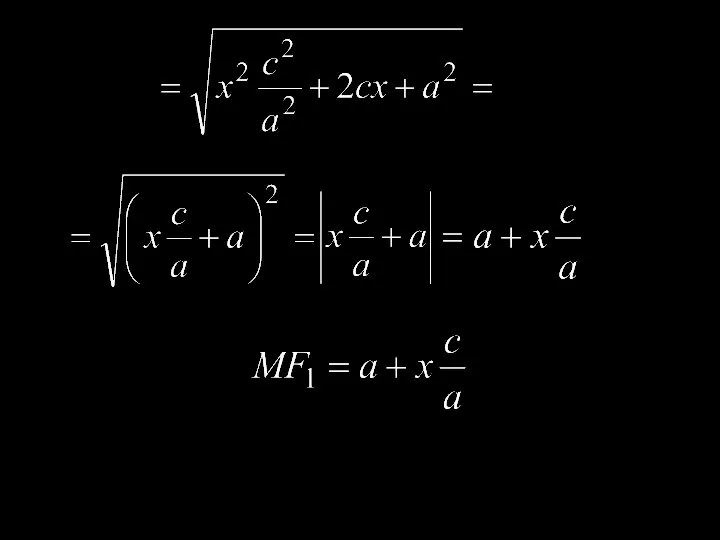


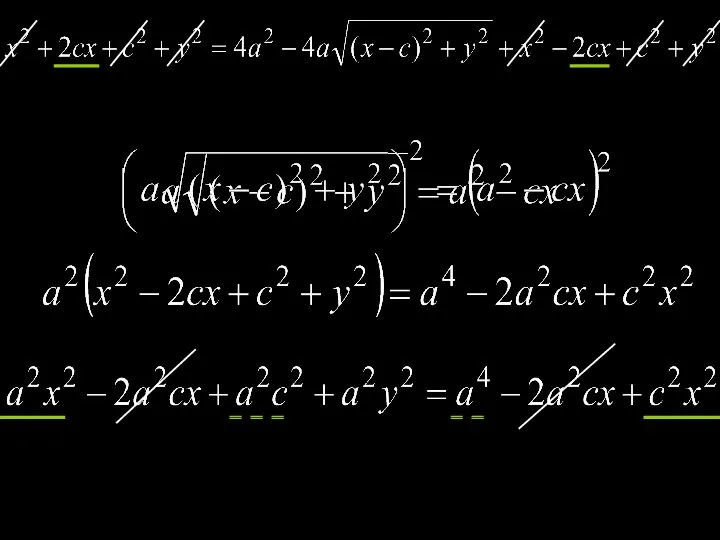


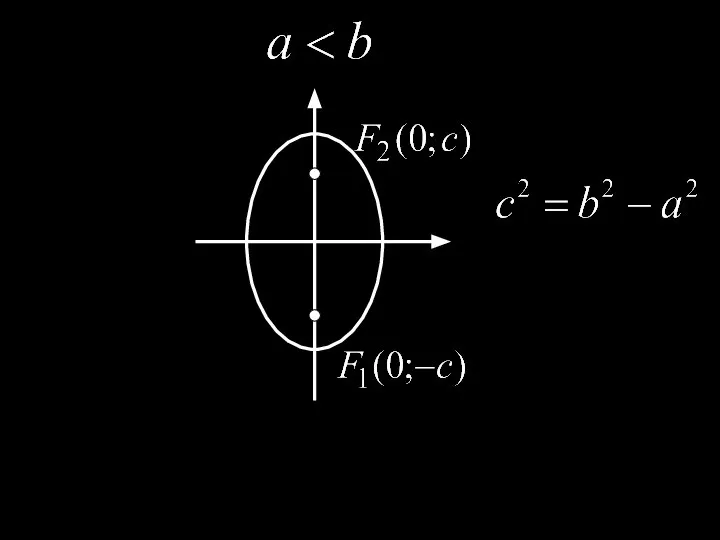











 Оценочная и сравнительная классификация алгоритмов
Оценочная и сравнительная классификация алгоритмов Теорема Пифагора. Квадрат гипотенузы равен сумме квадратов катетов
Теорема Пифагора. Квадрат гипотенузы равен сумме квадратов катетов Средние величины в юридической статистике
Средние величины в юридической статистике Подготовка к ЕГЭ (профильный уровень). Теория вероятности
Подготовка к ЕГЭ (профильный уровень). Теория вероятности Исследование функции при помощи производной
Исследование функции при помощи производной Математический магазин
Математический магазин Симметрия в нашей жизни
Симметрия в нашей жизни Решение систем неравенств второй степени с двумя переменными
Решение систем неравенств второй степени с двумя переменными Математика в профессии моих родителей
Математика в профессии моих родителей Геометрия, повторение
Геометрия, повторение Решение дробно-рациональных уравнений
Решение дробно-рациональных уравнений Использование приёма обобщения в процессе развития мышления учащихся
Использование приёма обобщения в процессе развития мышления учащихся Призма и ее виды
Призма и ее виды Арифметико-логические устройства. Устройства управления
Арифметико-логические устройства. Устройства управления Решение тригонометрических неравенств
Решение тригонометрических неравенств Область определения функции
Область определения функции Презентация на тему Перпендикуляр и наклонная
Презентация на тему Перпендикуляр и наклонная  Периметр квадрата
Периметр квадрата Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Интегральное исчисление
Интегральное исчисление Элементы теории множеств. Математические основы информатики
Элементы теории множеств. Математические основы информатики Интерактивный тренажёр. Сложение и вычитание в пределах первого десятка
Интерактивный тренажёр. Сложение и вычитание в пределах первого десятка Параллелепипед. Элементы параллелепипеда
Параллелепипед. Элементы параллелепипеда Презентация на тему Решение иррациональных уравнений
Презентация на тему Решение иррациональных уравнений  Тренировочные задания (графическое представление данных)
Тренировочные задания (графическое представление данных) Презентация на тему Среднее арифметическое, размах и мода
Презентация на тему Среднее арифметическое, размах и мода  Сложение и вычитание в пределах 20. 1 класс
Сложение и вычитание в пределах 20. 1 класс Площадь треугольника
Площадь треугольника