Funktsia_osnovnye_svoi_774_stva

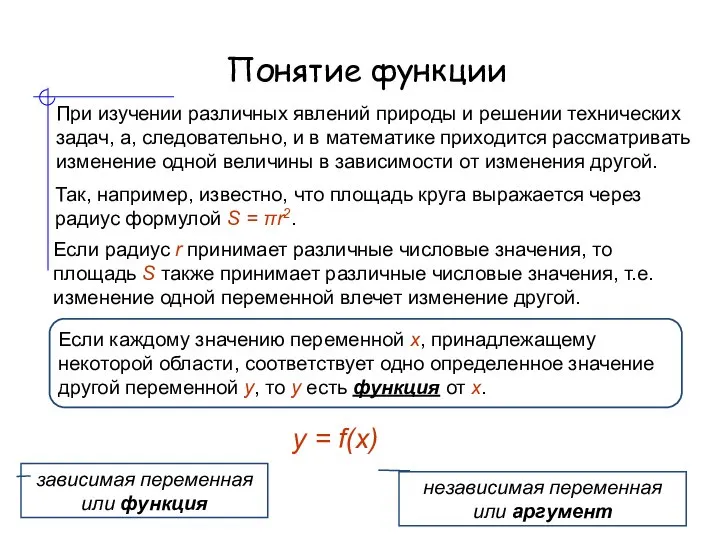
Понятие функции
При изучении различных явлений природы и решении технических задач, а, следовательно, и в математике приходится рассматривать изменение одной величины в зависимости от изменения другой.
Так, например, известно, что площадь круга выражается через радиус формулой S = πr2.
Если радиус r принимает различные числовые значения, то площадь S также принимает различные числовые значения, т.е. изменение одной переменной влечет изменение другой.
Если каждому значению переменной x, принадлежащему некоторой области, соответствует одно определенное значение другой переменной y, то y есть функция от х.
y = f(x)
независимая переменная или аргумент
зависимая переменная или функция

Понятие функции
Совокупность значений x, для которых определяются значения y в силу правила f(x) называется областью определения (областью существования) функции: D(f)
Совокупность значений y называется множеством значений функции: Е(f)
Способы задания функции:
1) Табличный.
При этом способе выписываются в определенном порядке значения аргумента и соответствующие им значения функции.

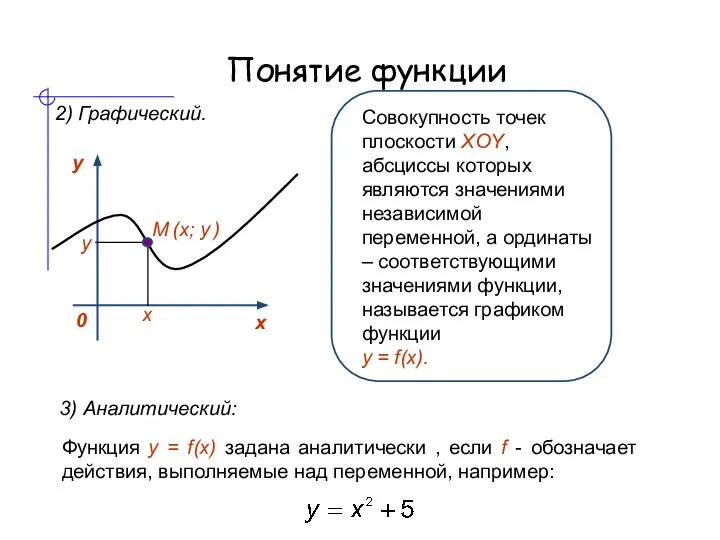
Понятие функции
2) Графический.
М (х; у )
Совокупность точек плоскости XOY, абсциссы которых являются значениями независимой переменной, а ординаты – соответствующими значениями функции, называется графиком функции
y = f(x).
х
y
3) Аналитический:
Функция y = f(x) задана аналитически , если f - обозначает действия, выполняемые над переменной, например:

Основные характеристики функции
Функция y = f(x) определенная на множестве D, называется четной, если для любого x, принадлежащего D выполняются условия: -x также принадлежит D и f(-x ) = f(x).
График четной функции симметричен относительно оси OY
Функция y = f(x) определенная на множестве D, называется нечетной, если:
График нечетной функции симметричен относительно точки O(0; 0)

Основные характеристики функции
то функция называется возрастающей.
Если
Если
то функция называется убывающей.
Если
то функция называется неубывающей.
Если
то функция называется невозрастающей.
Возрастающие, убывающие, невозрастающие и неубывающие функции называются монотонными на множестве D1, интервал, на котором функция монотонна называется интервалом монотонности.

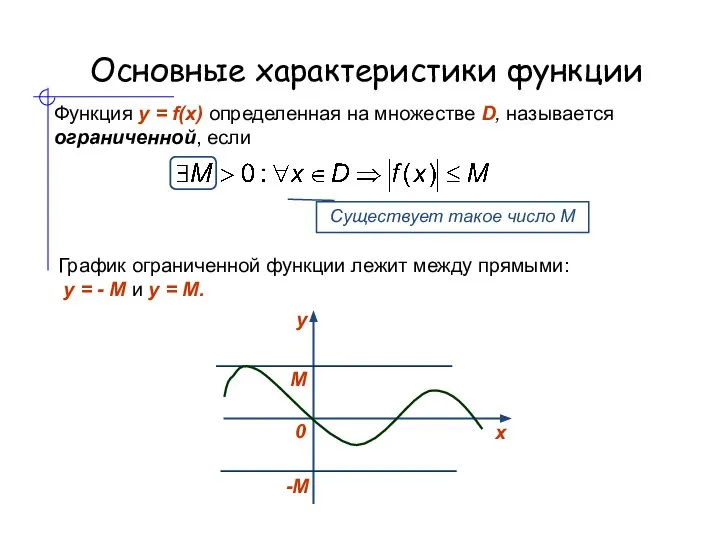
Основные характеристики функции
Функция y = f(x) определенная на множестве D, называется ограниченной, если
График ограниченной функции лежит между прямыми:
y = - M и y = M.
М
-М

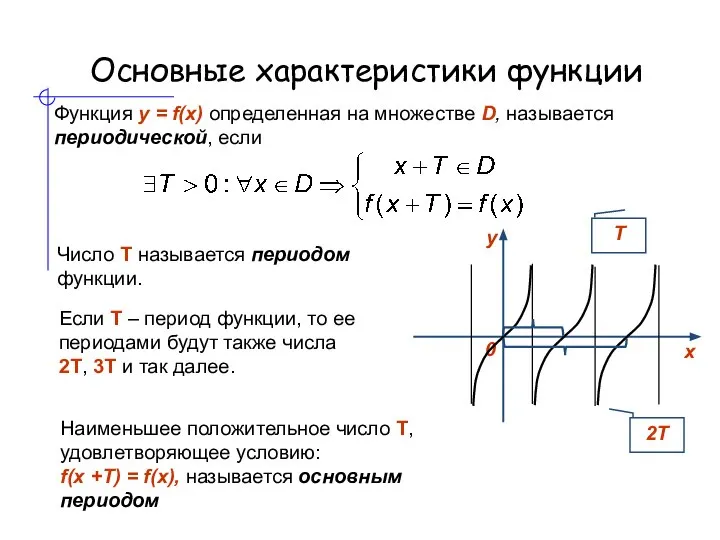
Основные характеристики функции
Функция y = f(x) определенная на множестве D, называется периодической, если
Число Т называется периодом функции.
Если Т – период функции, то ее периодами будут также числа 2Т, 3Т и так далее.
Наименьшее положительное число Т, удовлетворяющее условию:
f(x +T) = f(x), называется основным периодом

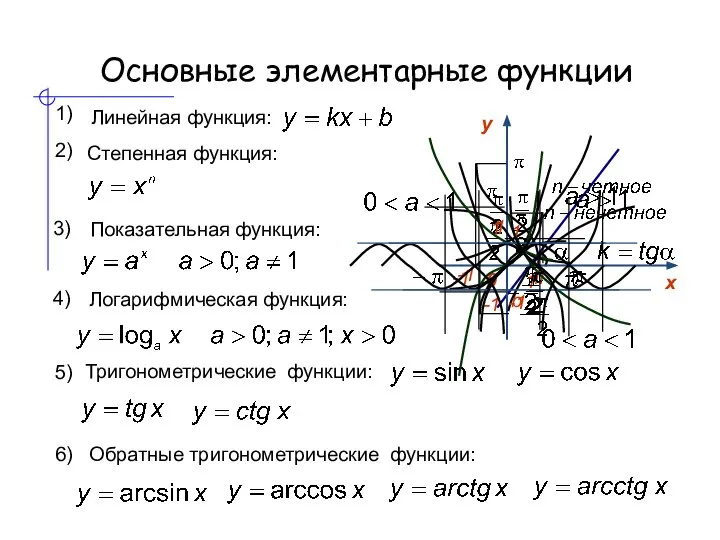
Основные элементарные функции
1)
Степенная функция:
2)
3)
4)
5)
Показательная функция:
Логарифмическая функция:
Линейная функция:
Тригонометрические функции:
6)
Обратные тригонометрические функции:

Сложная функция
Если y является функцией от u, а u в свою очередь зависит от переменной x, то y также зависит от x.
Сложная функция
Пример:
Областью определения функции является или вся область определения функции u(x) или та ее часть, в которой определяются значения u, не выходящие из области определения функции F(u).
Пример:

Элементарные функции
Элементарной функцией называется функция, которая может быть задана одной формулой вида y = f(x), где справа стоящее выражение составлено из основных элементарных функций и постоянных при помощи конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции.
Пример:

Алгебраические и трансцендентные функции
К числу алгебраических функций относятся элементарные функции следующего вида:
1)
Целая рациональная функция или многочлен:
2)
Дробная рациональная функция – отношение многочленов:
3)
Иррациональная функция:
Если в формуле y = f(x) в правой части производятся операции сложения, вычитания, умножения, деления и возведения в степень с рациональными нецелыми показателями, то функция y = f(x) называется иррациональной
Пример:
Функция, не являющейся алгебраической, называется трансцендентной: y = cos x; y = ln x и так далее.

Предел переменной величины
а
Пример:
Пусть переменная величина изменяется по закону:
Тогда: