Содержание
- 2. Чтобы построить график функции y=|f(x)|,надо сначала построить график функции y=f(x), а затем участки этого графика, лежащие
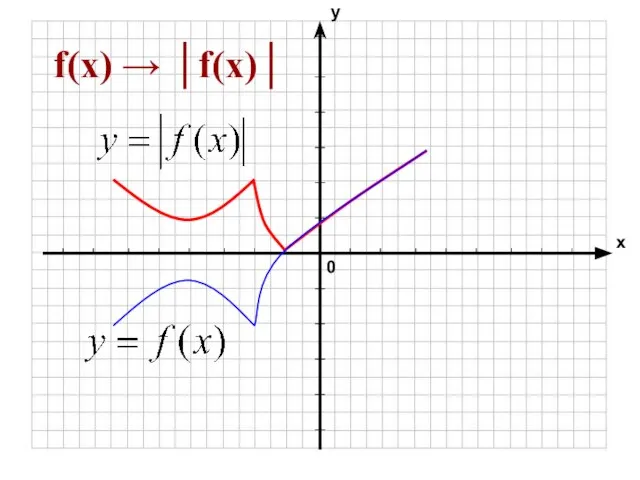
- 3. f(x) → │f(x)│
- 4. Так как f (|-x|) = f (|x|), то функция y = f (|x|) чётная и для
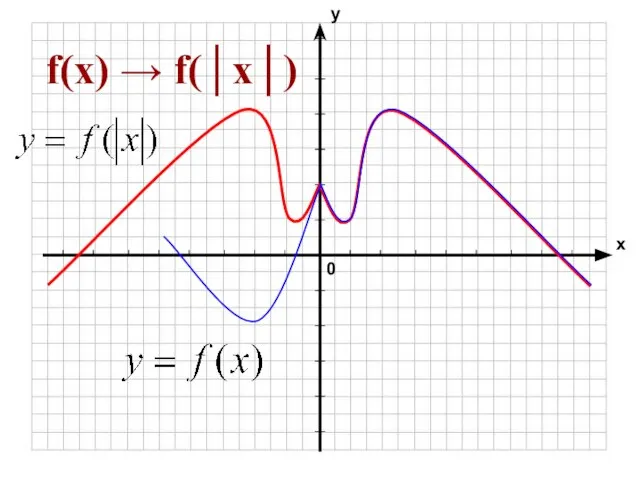
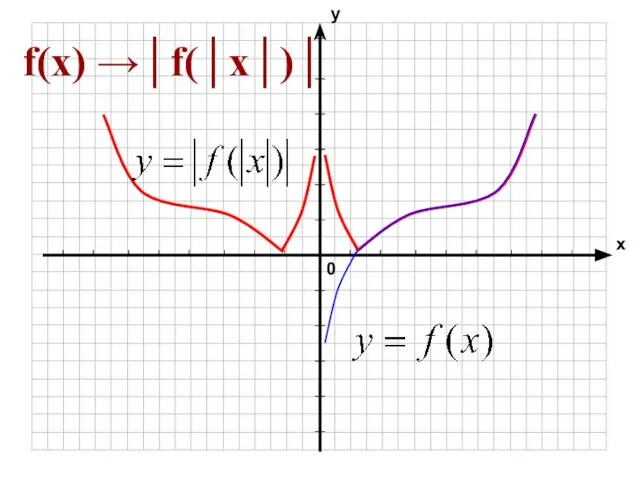
- 5. f(x) → f(│x│)
- 6. Построение графика функции у = |f(|x|)| Последовательность действий в этом случае представим следующим образом: построить график
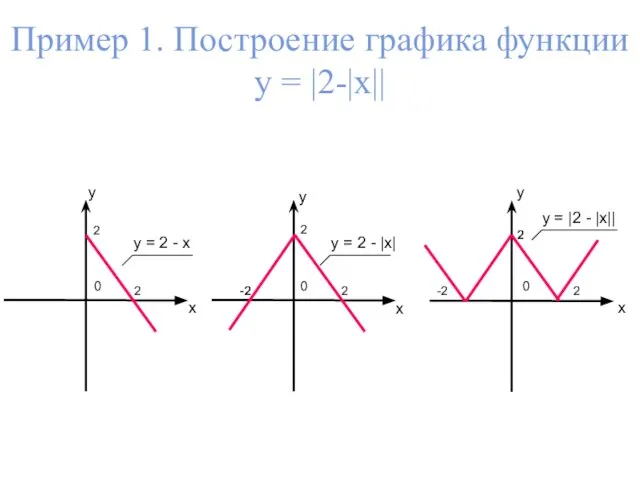
- 7. x y 0 y = 2 - x Пример 1. Построение графика функции у = |2-|x||
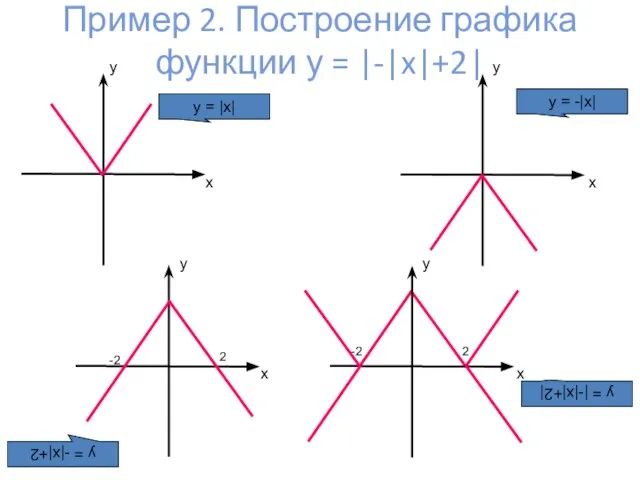
- 8. Пример 2. Построение графика функции у = |-|x|+2| y = |x| y = -|x| y =
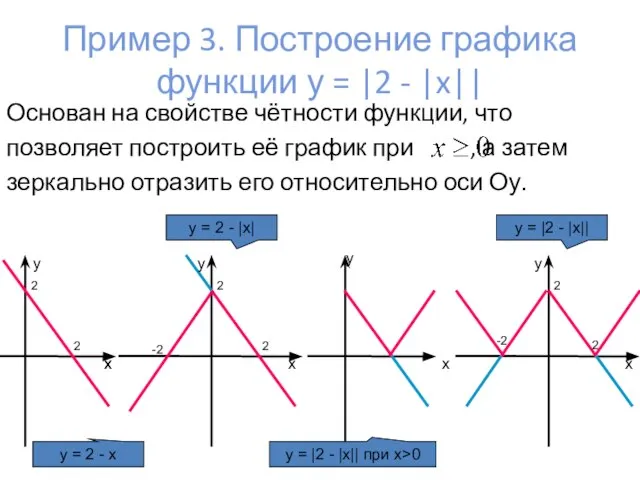
- 9. Пример 3. Построение графика функции у = |2 - |x|| Основан на свойстве чётности функции, что
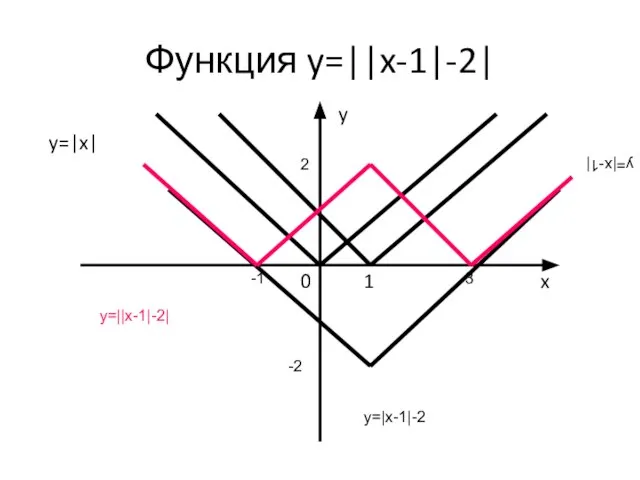
- 10. Функция y=||x-1|-2| Построение. 1)Строим график функции y=|x|. 2)Строим график функции y=|x-1|. 3)Строим график функции y= |x-1|-2.
- 11. Функция y=||x-1|-2| x y=|x| y 0 1 y=|x-1| -1 3 2 -2 y=|x-1|-2 y=||x-1|-2|
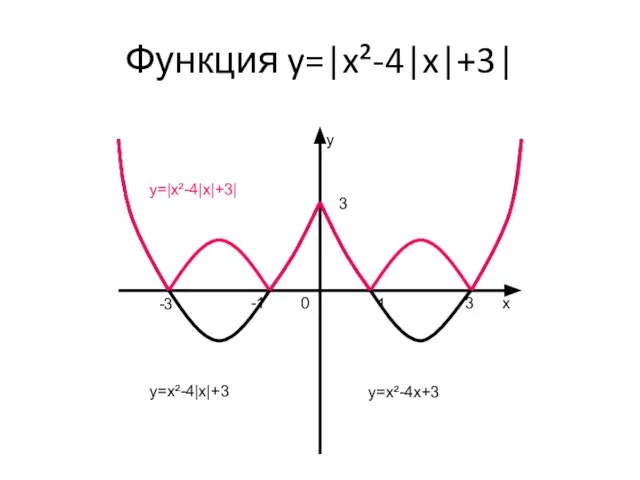
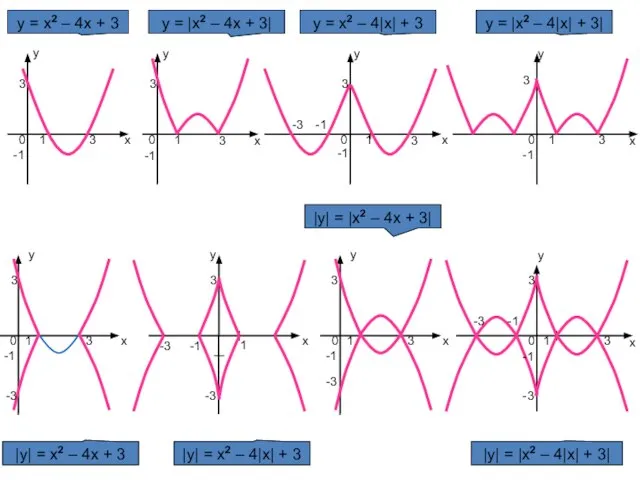
- 12. Функция y=|x²-4|x|-3| Построение. 1)Строим график y=x²-4x+3для х≥0 2)y=x²-4|x|+3 — отражаем полученный график в п.1 относительно оси
- 13. Функция y=|x²-4|x|+3| y x 0 -1 -3 1 3 3 y=x²-4x+3 y=x²-4|x|+3 y=|x²-4|x|+3|
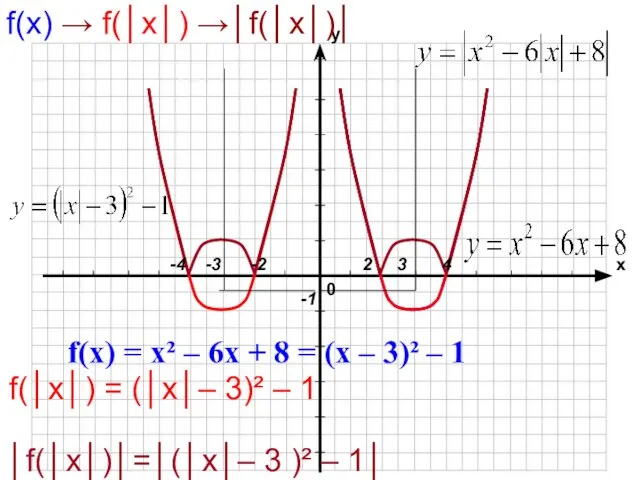
- 14. f(x) →│f(│x│)│
- 15. f(x) = x² – 6x + 8 = (x – 3)² – 1 f(│x│) = (│x│–
- 16. Построение графика функции |y| = f(x) при f(x) По определению абсолютной величины у = , где
- 17. Построение графиков функций |y| = |f(x)| Очевидно, что у = , т.е. график функции будет симметричен
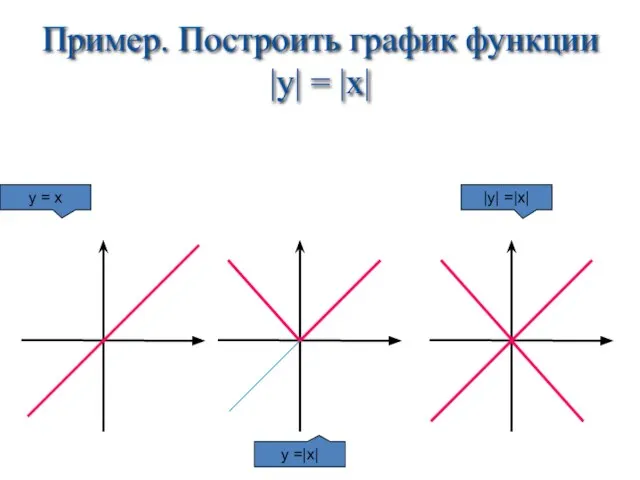
- 18. Пример. Построить график функции |y| = |x| y = x y =|x| |y| =|x|
- 19. Построение графиков функций вида y = |x – x1| + |x – x2| + ...+ |x
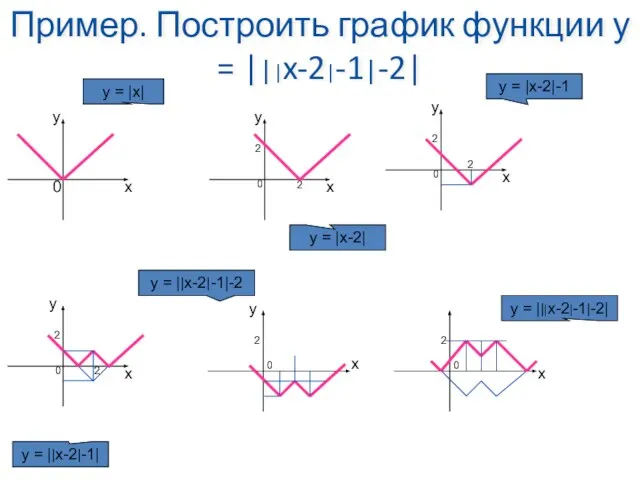
- 20. Пример. Построить график функции у = |||x-2|-1|-2| y х 0 y = |x| y х 0
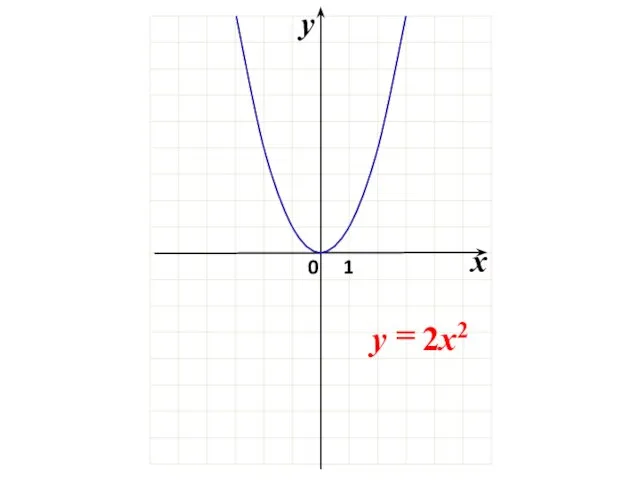
- 21. Пример 2. График функции y = x2 – 4x + 3
- 22. х y 0 1 3 -1 х y 0 1 3 -1 х y 0 1
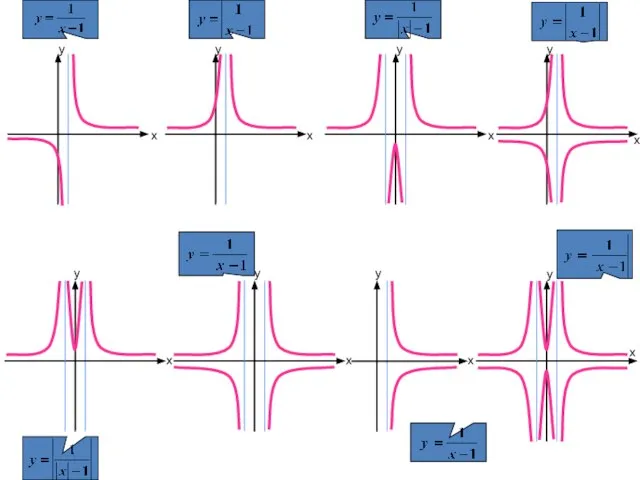
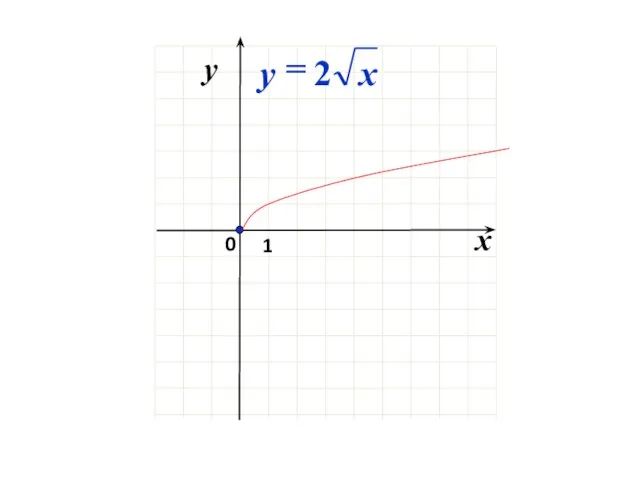
- 23. Пример 3. График функции 1 x-1 y =
- 24. х y х y х y х y х y х y х y х y
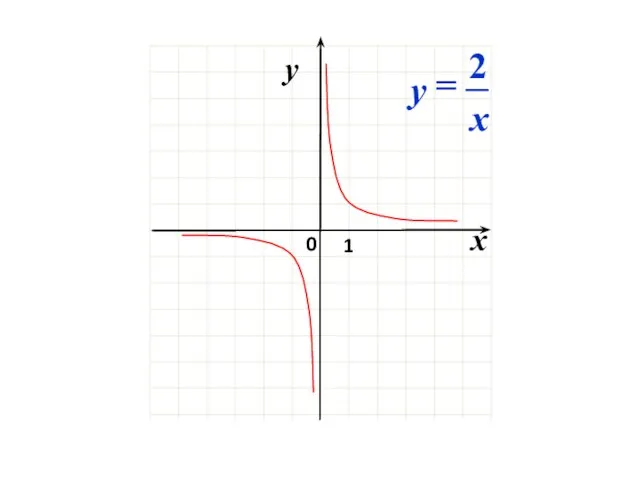
- 25. kk > 1 0
- 26. 0 x y 1
- 27. 0
- 28. 0 x y 1
- 29. x 0 y 1
- 31. k > 1
- 32. 0 x y 1
- 33. x 0 y 1
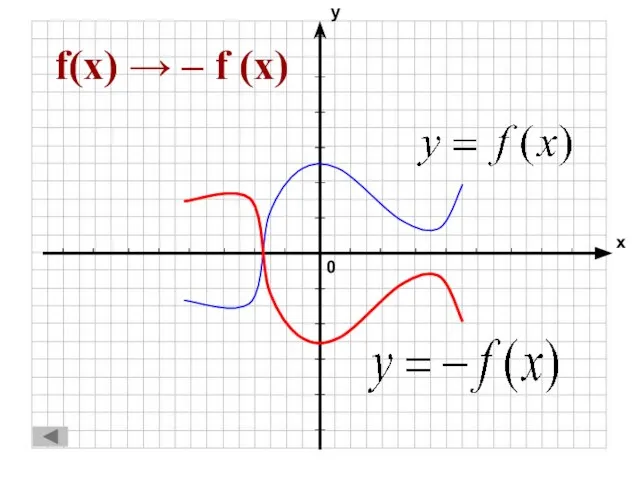
- 35. f(x) → – f (x)
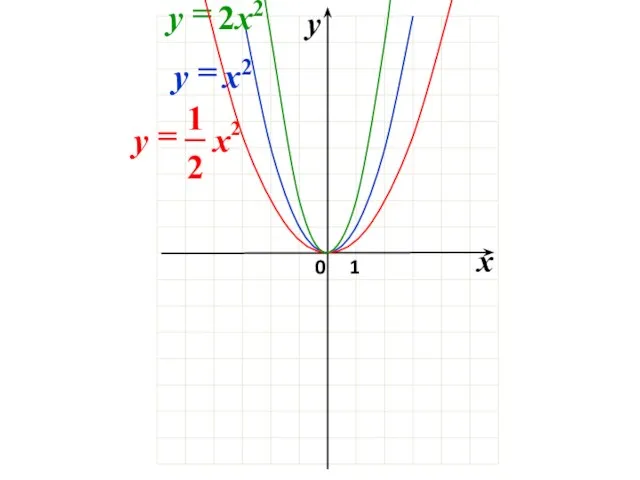
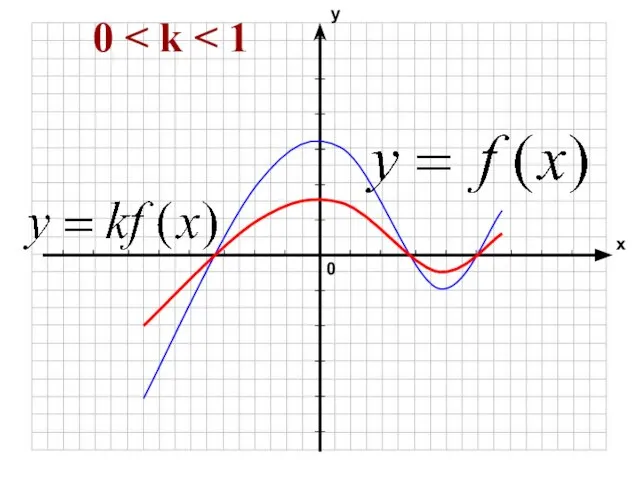
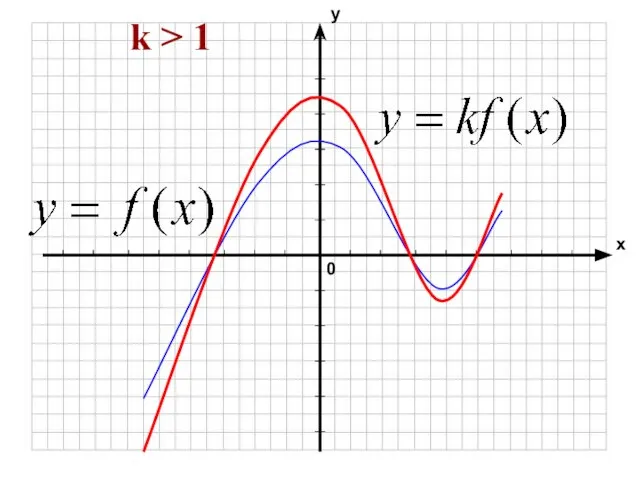
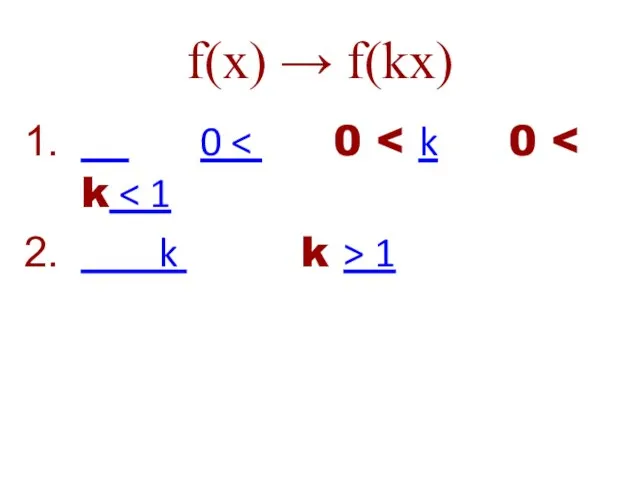
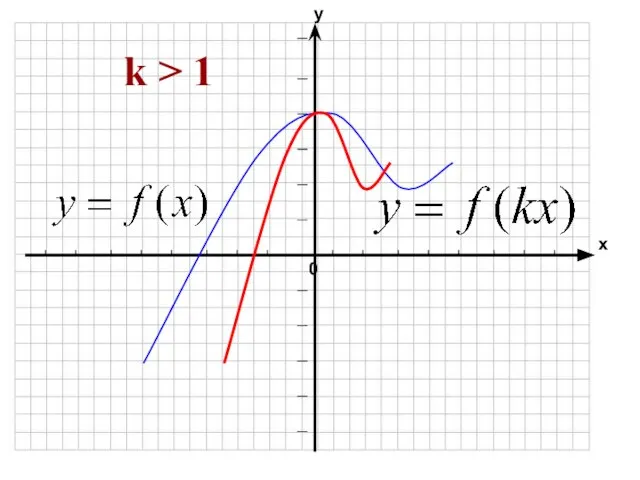
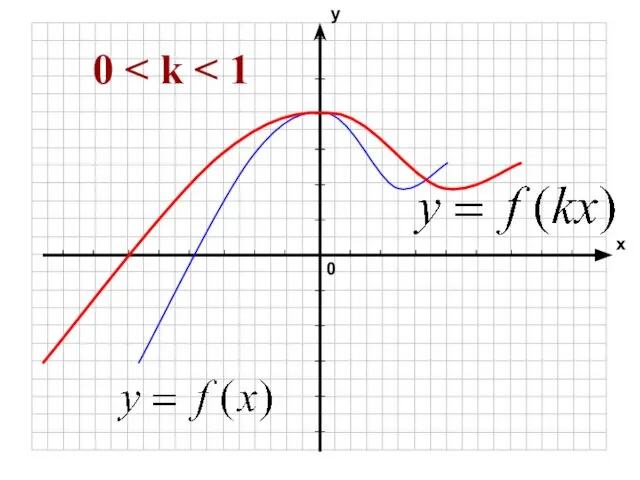
- 36. f(x) → f(kx) 0 k k > 1
- 37. k > 1
- 38. 0
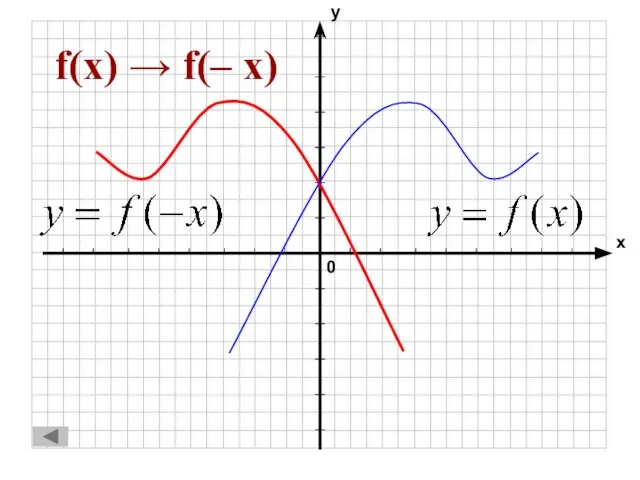
- 39. f(x) → f(– x)
- 41. Скачать презентацию










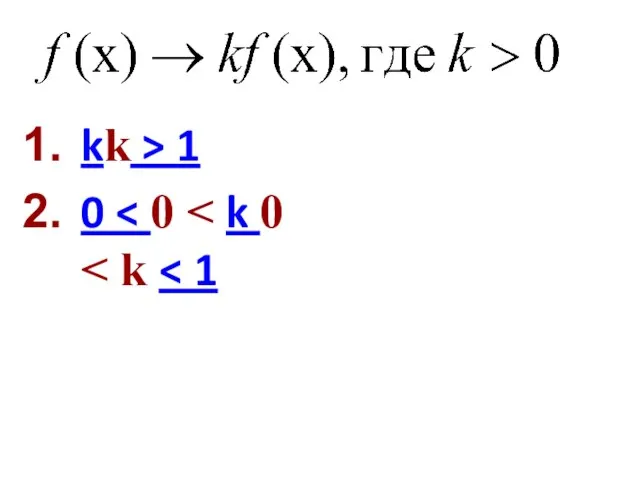
 Новогодняя викторина Я люблю математику I тур Арифметический
Новогодняя викторина Я люблю математику I тур Арифметический График линейной функции с модулем
График линейной функции с модулем Числовые промежутки
Числовые промежутки Исследование применения математического аппарата сетей Петри для моделирования процесса распределения инцидентов ИТ-службы
Исследование применения математического аппарата сетей Петри для моделирования процесса распределения инцидентов ИТ-службы Метод Галеркина для дифференциально-операторного уравнения третьего порядка
Метод Галеркина для дифференциально-операторного уравнения третьего порядка Памятка по оформлению краткой записи к задачам
Памятка по оформлению краткой записи к задачам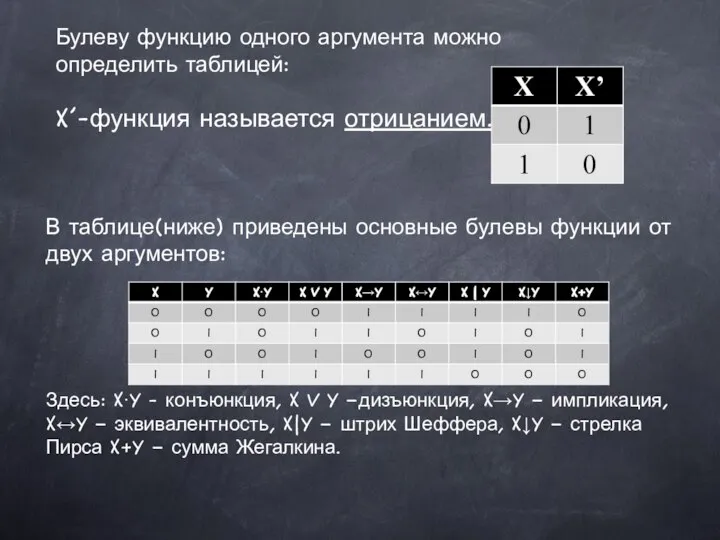 Булевы функции
Булевы функции Пропорциональность величин
Пропорциональность величин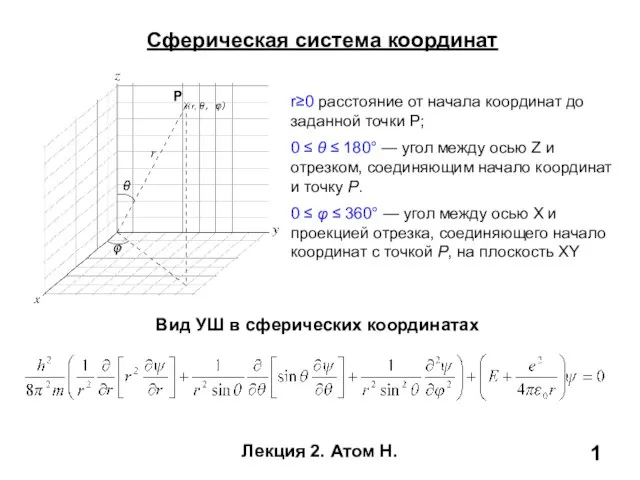 Сферическая система координат
Сферическая система координат История арабских чисел
История арабских чисел Квадратные уравнения
Квадратные уравнения Математика и я
Математика и я Дифференциальные исчисления функции одной независимой переменной
Дифференциальные исчисления функции одной независимой переменной Розв'язування типових задач
Розв'язування типових задач Знакомая незнакомка. Парабола
Знакомая незнакомка. Парабола Стереометрия. Основные фигуры в пространстве
Стереометрия. Основные фигуры в пространстве Возведение двучлена в любую натуральную степень
Возведение двучлена в любую натуральную степень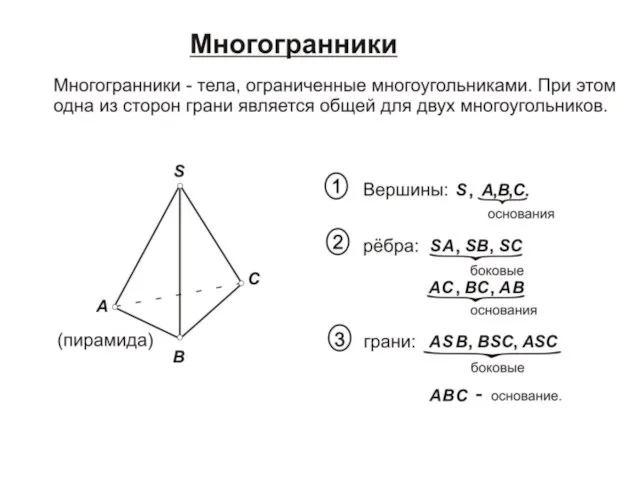 Многогранники + точки. Лекция 5
Многогранники + точки. Лекция 5 Метрология
Метрология Приемы письменных вычислений в пределах 1000. 3 класс
Приемы письменных вычислений в пределах 1000. 3 класс Ikeldilen argumentiň trigonometrik funksiýalary
Ikeldilen argumentiň trigonometrik funksiýalary Физический и геометрический смысл производной. Понятие дифференциал функции
Физический и геометрический смысл производной. Понятие дифференциал функции Выражение F
Выражение F Показательные уравнения и неравенства
Показательные уравнения и неравенства Умножение обыкновенных дробей
Умножение обыкновенных дробей Практико-ориентированное задание
Практико-ориентированное задание Веб – квест для учащихся 11 класса. Задачи по теме Производная
Веб – квест для учащихся 11 класса. Задачи по теме Производная Периметр многогранника
Периметр многогранника