Линейная алгебра. (Матрицы, определители)

ЛИНЕЙНАЯ АЛГЕБРА

МАТРИЦА

КВАДРАТНАЯ МАТРИЦА

ДИАГОНАЛЬНАЯ МАТРИЦА

ЕДИНИЧНАЯ МАТРИЦА

A1xn =( a 11 a 12 … a1n)
(6 -8 0 7 )

ТРАНСПОНИРОВАННАЯ МАТРИЦА

СУММА МАТРИЦ

РАЗНОСТЬ МАТРИЦ

СВОЙСТВА СУММЫ МАТРИЦ
A+B=B+A;
(A+B)+C=A+(B+C);
A+0=A;
A+(- A)=0.

УМНОЖЕНИЕ МАТРИЦЫ НА ЧИСЛО

СВОЙСТВА ПРОИЗВЕДЕНИЯ МАТРИЦЫ НА ЧИСЛО
1⋅A =A
(??)A=?(?A)
(?+?)A=?A+?A
?(A+B)=?A+?B

ПРОИЗВЕДЕНИЕ МАТРИЦ
Amxn⋅Bnxp=Cmxp

СВОЙСТВА ПРОИЗВЕДЕНИЯ МАТРИЦ
(AB)C=A(BC)
AB≠BA
AE=EA
(A+B)C=AC+BC; A(B+C)=AB+AC
(kA)B=k(AB)=A(kB)

ОПРЕДЕЛИТЕЛЬ

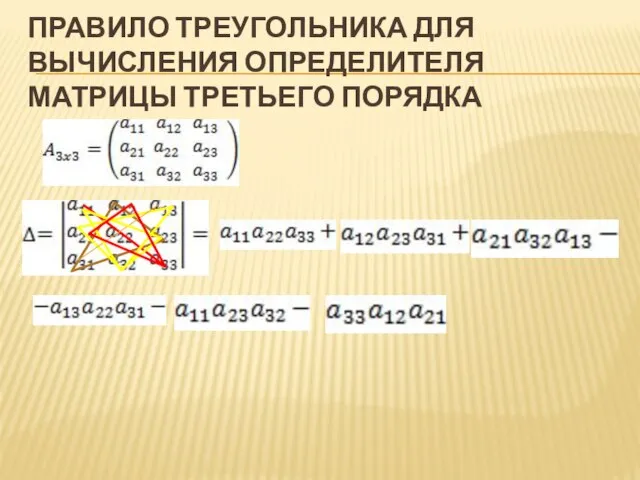
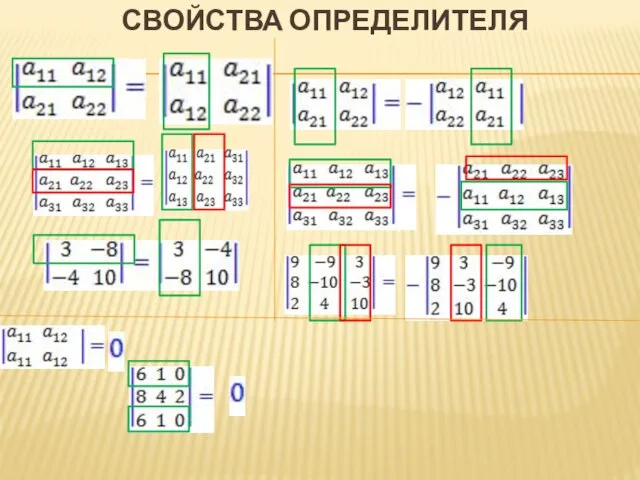
ПРАВИЛО ТРЕУГОЛЬНИКА ДЛЯ ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЯ МАТРИЦЫ ТРЕТЬЕГО ПОРЯДКА

ПРАВИЛО САРРЮСА

СВОЙСТВА ОПРЕДЕЛИТЕЛЯ

МИНОР
Mij
M21 = a12
M11 = 7

АЛГЕБРАИЧЕСКОЕ ДОПОЛНЕНИЕ
Aij
Aij = (-1)i+j⋅Mij
матрицы
=
=+642.

РАЗЛОЖЕНИЕ ОПРЕДЕЛИТЕЛЯ ПО СТРОКЕ ИЛИ СТОЛБЦУ
(

РАНГ МАТРИЦЫ A (RANGA)
rangA=3