Содержание
- 2. УЧЕБНЫЕ ВОПРОСЫ: 1. Марковские случайные процессы с дискретными состояниями и непрерывным временем. 2. Предельные вероятности состояний.
- 3. Вопрос 1. Марковские случайные процессы с дискретными состояниями и непрерывным временем
- 4. Процессы в системах с дискретными состояниями, меняющимися в случайные моменты времени, называются случайными процессами с дискретными
- 5. Вместо переходных вероятностей Pij вводятся плотности вероятностей перехода λij. Пусть система S в момент времени t
- 6. Плотность вероятности перехода λij описывается выражением: (1) где Pij(∆t) – вероятность того, что система, находившаяся в
- 7. Из (1) следует, что при малом ∆t Это выражение справедливо для стационарных процессов, когда вероятность перехода
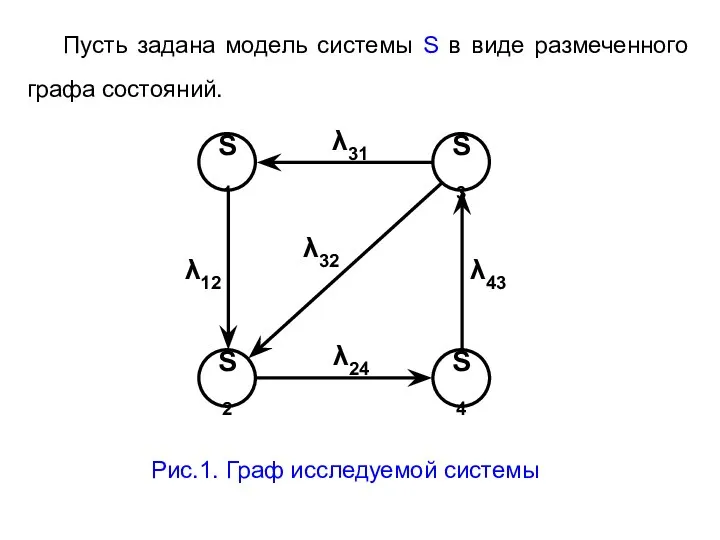
- 8. Пусть задана модель системы S в виде размеченного графа состояний. Рис.1. Граф исследуемой системы
- 9. Рассмотрим момент времени t. Придадим t малое приращение ∆t и найдем P1(t+∆t) – вероятность того, что
- 10. Это может произойти в двух случаях (см. рис. 1): 1) в момент t система была в
- 11. Вероятность первого случая найдем как произведение вероятности Р1(t) того, что в момент t система была в
- 12. Вероятность второго случая равна вероятности того, что в момент t система была в S3, умноженной на
- 13. Применим правило сложения вероятностей: Раскроем скобки в правой части, перенесем Р1(t) в левую и разделим обе
- 14. Устремим ∆t к нулю и перейдем к пределу: Левая часть – производная функции Р1(t): (2)
- 15. Для вероятностей остальных состояний такие уравнения получим аналогично. Запишем их, отбросив для краткости аргумент t у
- 16. (3)
- 17. Уравнения (3) называют уравнениями Колмогорова. Интегрирование данной системы уравнений даст нам искомые вероятности состояний как функции
- 18. Начальные условия определяются исходным состоянием системы. Например, если при t = 0 система была в состоянии
- 19. Одно из дифференциальных уравнений в системе (3) может быть заменено на балансное алгебраическое уравнение: так как
- 20. 1. В левой части уравнения стоит производная вероятности состояния системы по времени. 2. В правой части
- 21. 3. Каждое слагаемое равно произведению плотности вероятности перехода, записанной возле стрелки, умноженной на вероятность того состояния,
- 22. Вопрос 2. Предельные вероятности состояний системы
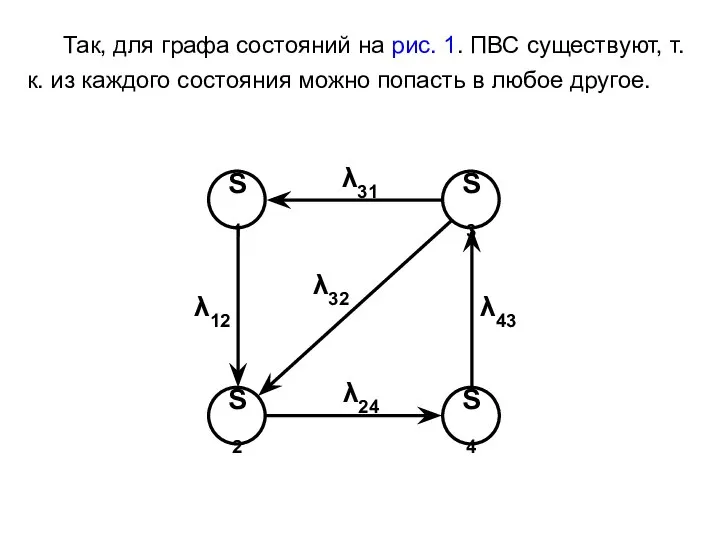
- 23. Если: 1) число состояний системы конечно; 2) из каждого состояния можно перейти в любое другое, то
- 24. Для вычисления ПВС необходимо: 1) в системе уравнений Колмогорова положить левые части (производные вероятностей состояний) равными
- 25. Так, для графа состояний на рис. 1. ПВС существуют, т.к. из каждого состояния можно попасть в
- 26. Приравняем левые части уравнений системы (3) нулю и перенесем туда отрицательные слагаемые: (4)
- 27. Для решения системы (4) одно из ее уравнений заменим на балансное. Решив ее, получим значения ПВС.
- 29. Скачать презентацию













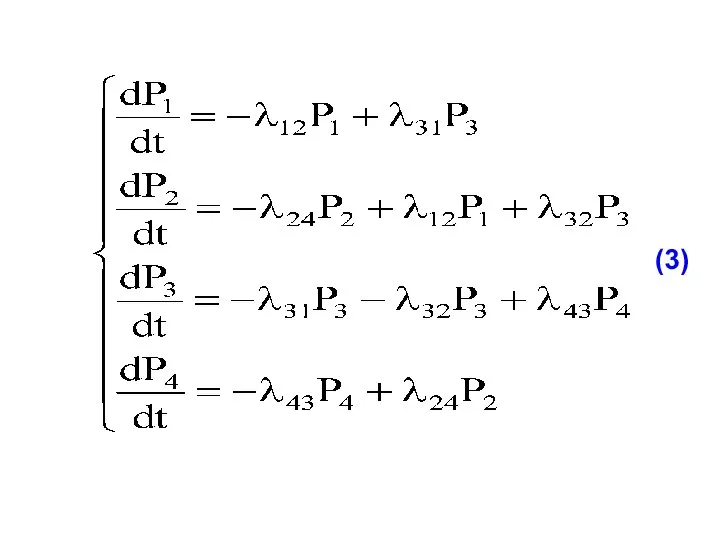










 Скалярное произведение векторов
Скалярное произведение векторов Линейные неравенства
Линейные неравенства Сравнительный анализ лирики А.С. Пушкина и В.В. Маяковского методами математической статистики
Сравнительный анализ лирики А.С. Пушкина и В.В. Маяковского методами математической статистики О числах
О числах Интегралы Фруллани
Интегралы Фруллани Способ группировки
Способ группировки Площадь параллелограмма
Площадь параллелограмма Элементы теории вероятности
Элементы теории вероятности Определение арифметической прогрессии
Определение арифметической прогрессии Числовые неравенства
Числовые неравенства Систематизация учебного материала по алгебре и началам анализа в 11 классе для организации повторения
Систематизация учебного материала по алгебре и началам анализа в 11 классе для организации повторения Решение треугольников
Решение треугольников Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже
Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже Математика и здоровье
Математика и здоровье Суммы чисел
Суммы чисел Математика в профессии строителя
Математика в профессии строителя Способы решения тригонометрических уравнений
Способы решения тригонометрических уравнений Метод искусственного базиса
Метод искусственного базиса Сложение и вычитание
Сложение и вычитание Теорема о свойстве биссектрисы с доказательством
Теорема о свойстве биссектрисы с доказательством Математические задания
Математические задания Презентация на тему Приближённые вычисления
Презентация на тему Приближённые вычисления  Аксонометрические проекции плоских фигур
Аксонометрические проекции плоских фигур Все ли в мире состоит из многогранников
Все ли в мире состоит из многогранников Перестановка слагаемых
Перестановка слагаемых Понятие вектор
Понятие вектор Комплексные числа и координатная плоскость
Комплексные числа и координатная плоскость Полулогарифмические модели
Полулогарифмические модели