Содержание
- 2. Исследование функции с помощью производной Сальтяшева А.И., ГБОУ НПО ПУ № 19, г.Салават. www.uchportal.ru
- 3. УСТНЫЙ ОПРОС Достаточный признак возрастания функции. Достаточный признак убывания функции. Какие точки области определения функции являются
- 4. Достаточный признак возрастания функции Если функция f имеет неотрицательную производную в каждой точке интервала (а;b), то
- 5. Достаточный признак убывания функции Если функция f имеет неположительную производную в каждой точке интервала (а;b), то
- 6. Необходимое условие экстремума (Теорема Ферма) Если точка х0 является точкой экстремума функции f и в этой
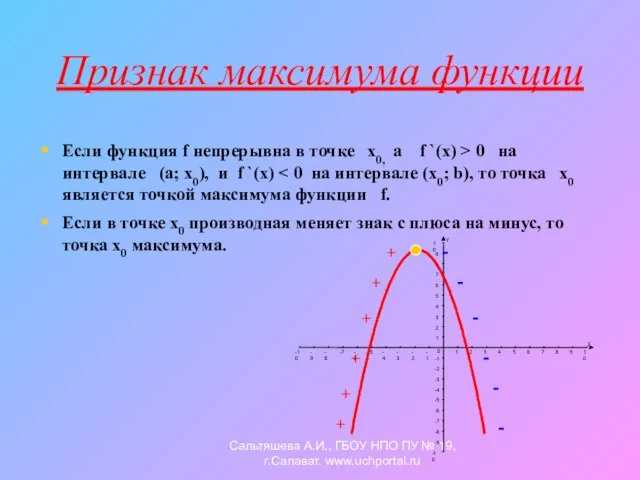
- 7. Признак максимума функции Если функция f непрерывна в точке х0, а f `(x) > 0 на
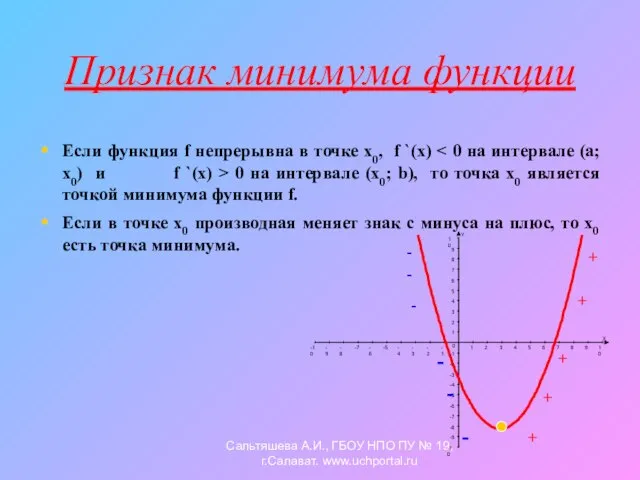
- 8. Признак минимума функции Если функция f непрерывна в точке х0, f `(x) 0 на интервале (х0;
- 9. Практическая работа Найти промежутки возрастания и убывания функции, точки экстремума Сальтяшева А.И., ГБОУ НПО ПУ №
- 10. 1. Какова область определения функции? 2. Найдите область определения функции Сальтяшева А.И., ГБОУ НПО ПУ №
- 11. 3. Какая это функция: четная или нечетная? Сальтяшева А.И., ГБОУ НПО ПУ № 19, г.Салават. www.uchportal.ru
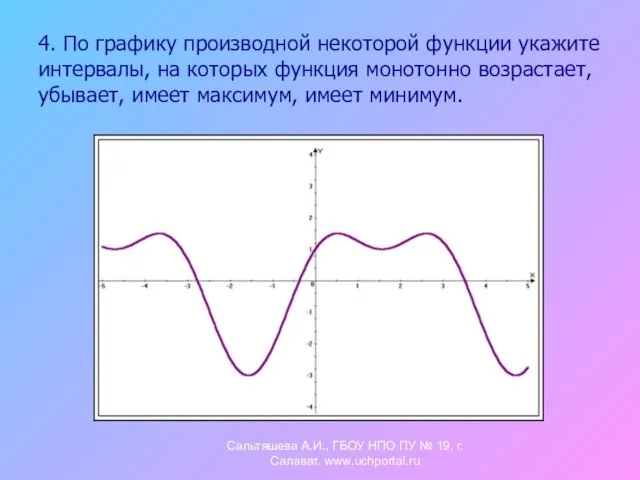
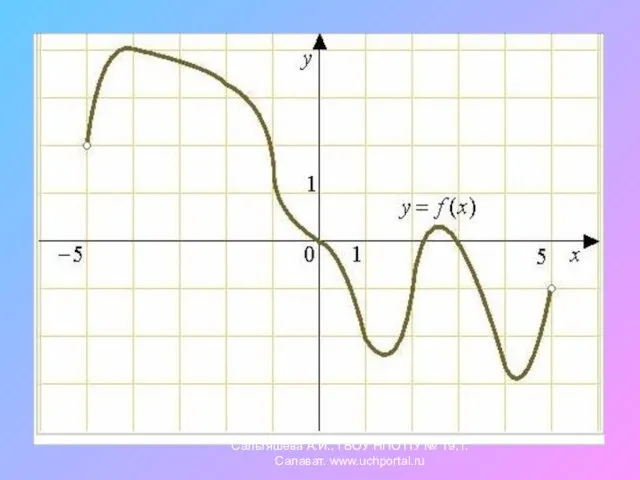
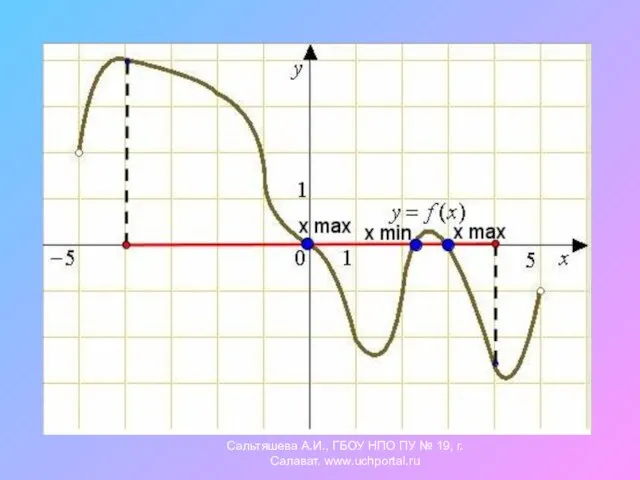
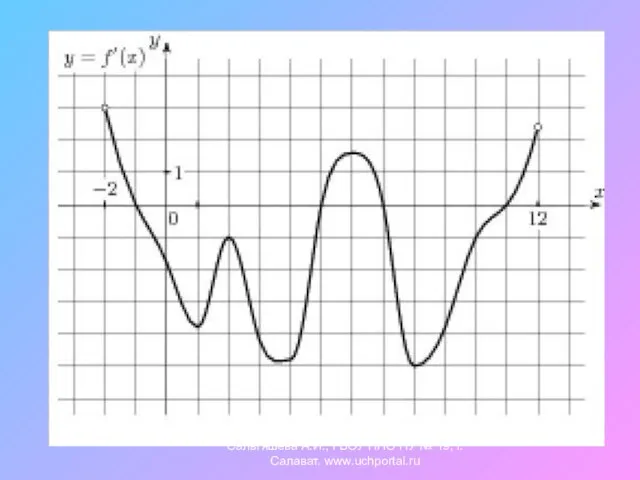
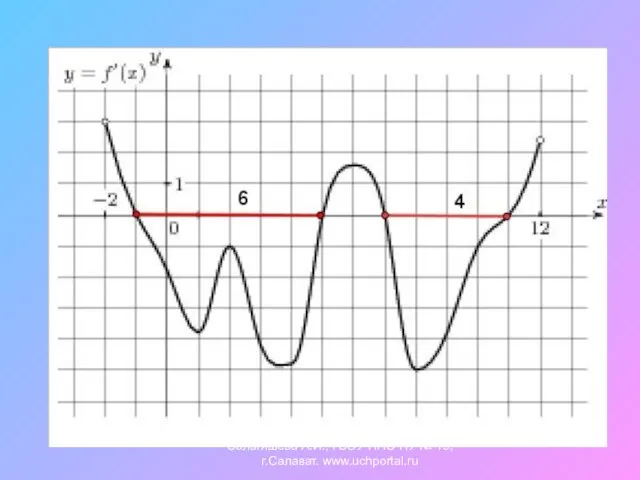
- 12. 4. По графику производной некоторой функции укажите интервалы, на которых функция монотонно возрастает, убывает, имеет максимум,
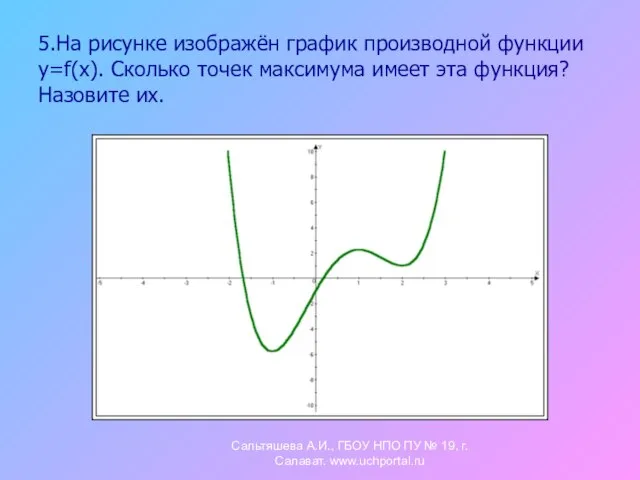
- 13. 5.На рисунке изображён график производной функции y=f(x). Сколько точек максимума имеет эта функция? Назовите их. Сальтяшева
- 14. ЛЕОНАРД ЭЙЛЕР (1707-1783) Математик, механик, физик и астроном. По происхождению швейцарец. В 1726 был приглашен в
- 15. СХЕМА ИССЛЕДОВАНИЯ ГРАФИКА ФУНКЦИИ Найти область определения функции. (Указать множество значений переменной х, при которых данная
- 16. ПРИМЕР Исследовать функцию и построить график Сальтяшева А.И., ГБОУ НПО ПУ № 19, г.Салават. www.uchportal.ru
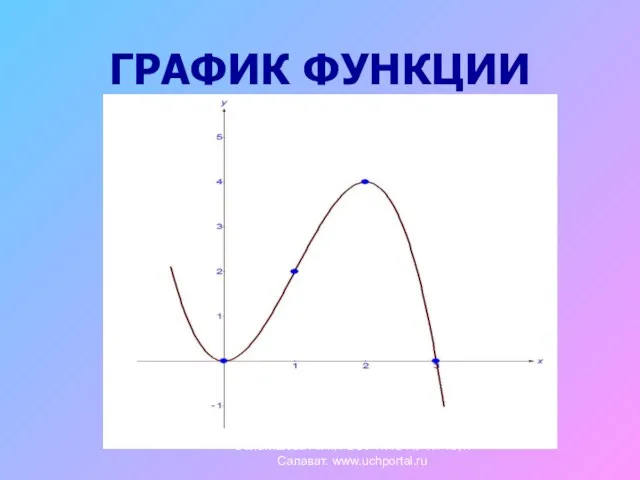
- 17. ГРАФИК ФУНКЦИИ Сальтяшева А.И., ГБОУ НПО ПУ № 19, г.Салават. www.uchportal.ru
- 18. ФИЗКУЛЬТМИНУТКА Сальтяшева А.И., ГБОУ НПО ПУ № 19, г.Салават. www.uchportal.ru
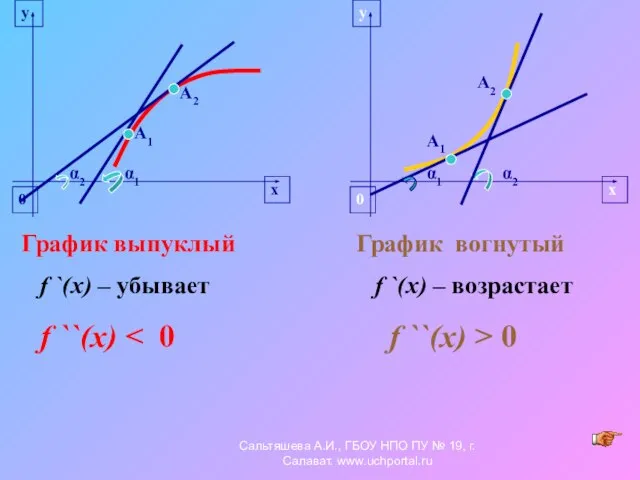
- 19. α1 α2 График выпуклый f `(x) – убывает f ``(x) График вогнутый f `(x) – возрастает
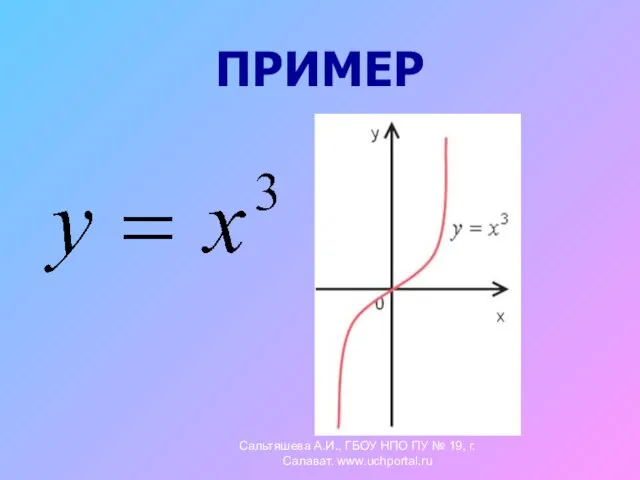
- 20. ПРИМЕР Сальтяшева А.И., ГБОУ НПО ПУ № 19, г.Салават. www.uchportal.ru
- 21. ПРАКТИЧЕСКАЯ РАБОТА Найти интервалы выпуклости и точку перегиба, если Сальтяшева А.И., ГБОУ НПО ПУ № 19,
- 22. Сальтяшева А.И., ГБОУ НПО ПУ № 19, г.Салават. www.uchportal.ru
- 23. Сальтяшева А.И., ГБОУ НПО ПУ № 19, г.Салават. www.uchportal.ru
- 24. Сальтяшева А.И., ГБОУ НПО ПУ № 19, г.Салават. www.uchportal.ru
- 25. Сальтяшева А.И., ГБОУ НПО ПУ № 19, г.Салават. www.uchportal.ru
- 26. ТВОРЧЕСКОЕ ЗАДАНИЕ Я – функция сложная, это известно, Еще расскажу, если вам интересно, Что точку разрыва
- 27. ДОМАШНЕЕ ЗАДАНИЕ 1. № 300 (а, б). 2. Нестандартное задание: найдите функции, описывающие реальные физические процессы,
- 28. ИТОГ УРОКА Рассмотрите взаимосвязь между свойством функции и производной. Как влияет знак второй производной на выпуклость
- 30. Скачать презентацию















 Упрощение логических операций
Упрощение логических операций Теорема Пифагора
Теорема Пифагора История системы мер длины (часть 2)
История системы мер длины (часть 2) Probability Distributions
Probability Distributions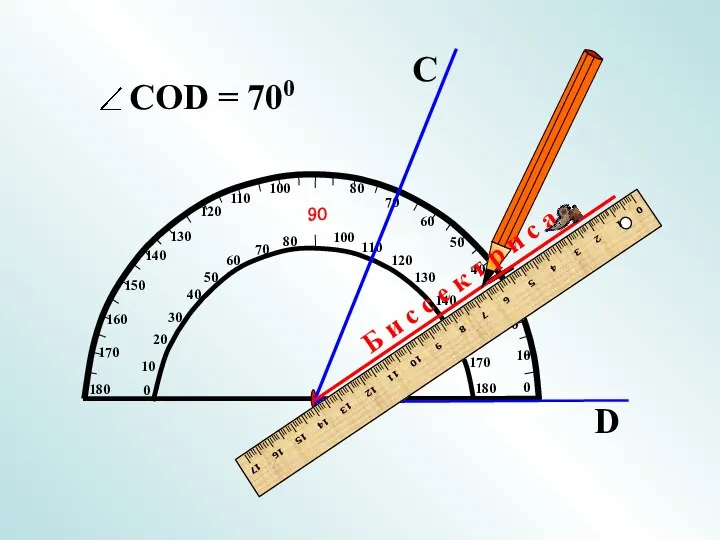 Биссектриса угла
Биссектриса угла Деление вида a:а, а:1
Деление вида a:а, а:1 Прямоугольник, ромб, квадрат
Прямоугольник, ромб, квадрат Понятие вектора. Равенство векторов
Понятие вектора. Равенство векторов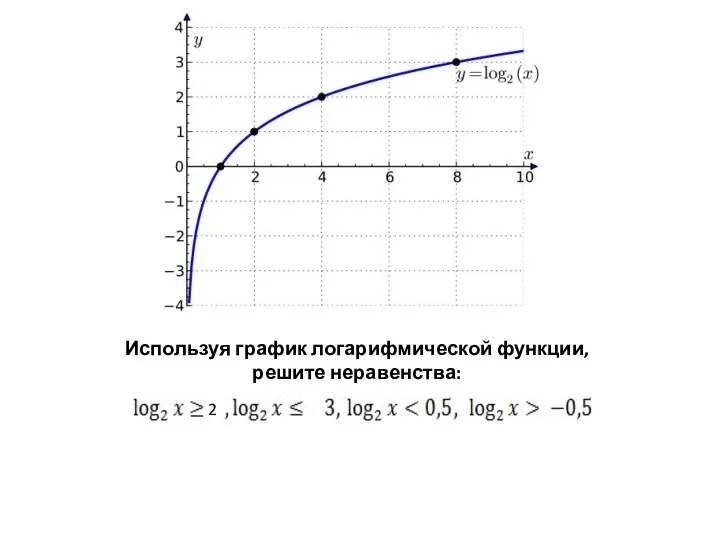 Логарифмические неравенства. устные упражнения
Логарифмические неравенства. устные упражнения Матрица размера m x n
Матрица размера m x n Тренажер Состав числа
Тренажер Состав числа Отношения и золотое сечение
Отношения и золотое сечение Параллелограмм и его свойства и признаки
Параллелограмм и его свойства и признаки Страна Математика
Страна Математика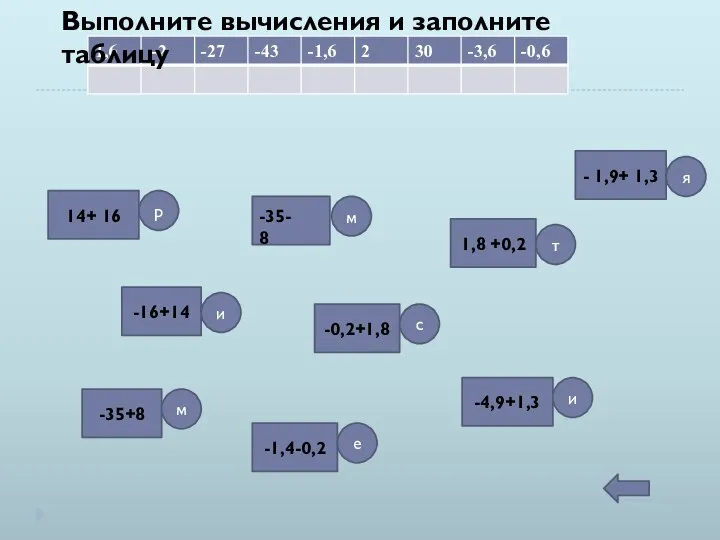 Выполните вычисления и заполните таблицу. 6 класс
Выполните вычисления и заполните таблицу. 6 класс Матрицы и определители
Матрицы и определители Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Веселое путешествие
Веселое путешествие Есептер шығару
Есептер шығару Наши истинные учителя опыт и чувства. Из истории геометрии
Наши истинные учителя опыт и чувства. Из истории геометрии Параллельность прямых. Урок – практикум
Параллельность прямых. Урок – практикум Определение равнодействующей и уравновешивающих сходящихся сил плоской системы сил графическим и аналитическим способами
Определение равнодействующей и уравновешивающих сходящихся сил плоской системы сил графическим и аналитическим способами Проект по математике Задачи-расчеты из моей жизни
Проект по математике Задачи-расчеты из моей жизни Приближение вычисления
Приближение вычисления Пирамида. Усеченная пирамида
Пирамида. Усеченная пирамида Смешаное число
Смешаное число Состав числа (домики)
Состав числа (домики) Сопоставление эмпирических и теоретических частот
Сопоставление эмпирических и теоретических частот