Содержание
- 2. ИСТРИЯ ПОЯВЛЕНИЯ ЛОГАРИФМА
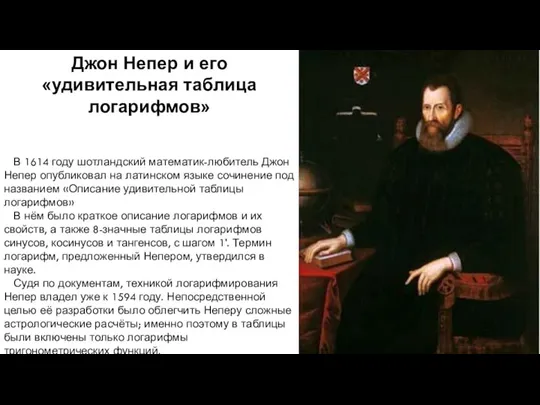
- 3. Джон Непер и его «удивительная таблица логарифмов» В 1614 году шотландский математик-любитель Джон Непер опубликовал на
- 4. ЧТО ТАКОЕ ЛОГАРИФМ?
- 5. Логарифм числа b по основанию a определяется как показатель степени, в которую надо возвести основание a,
- 6. СВОЙСТВА ЛОГАРИФМА
- 11. 5. Логарифм произведения b на c по основанию a Если число логарифма является произведением, то его
- 12. 6. Логарифм деления b на c по основанию a Если число логарифма является делением, то его
- 13. 7. a в степени логарифм числа b по основанию a Если основание логарифма совпадает с числом,
- 14. 8. Произведение зеркальных логарифмов Если логарифм, основание которого равен числу другого логарифма, основание другого логарифма ровняется
- 15. 9. Обмен числа и основания логарифма Если перевернуть логарифм, то число можно убрать в основание, а
- 16. 10. Замена числа в основании логарифма Если нужно другое основание логарифма, то можно представить его как
- 18. Скачать презентацию





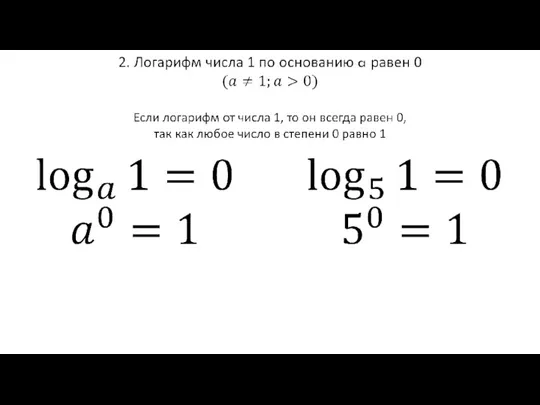







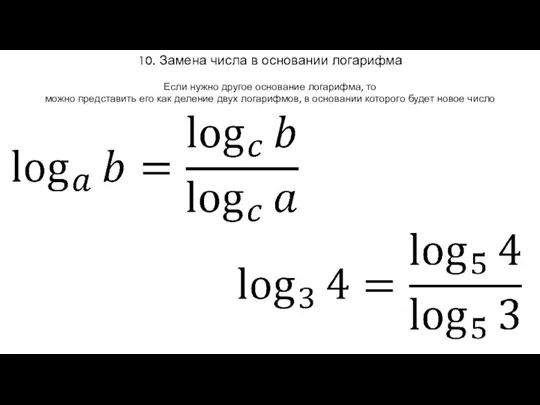
 Решение систем линейных неравенств
Решение систем линейных неравенств Построение сечений
Построение сечений Credit and exam
Credit and exam Решение задач с помощью уравнений. Урок математики в 5 классе
Решение задач с помощью уравнений. Урок математики в 5 классе Объемы тел. Подготовка к контрольной работе
Объемы тел. Подготовка к контрольной работе Вероятность события
Вероятность события Сумма
Сумма Эконометрка ва омори риёзи
Эконометрка ва омори риёзи Способы решения систем линейных уравнений
Способы решения систем линейных уравнений Симметрия в окружающем мире
Симметрия в окружающем мире Презентация на тему Число и цифра 5
Презентация на тему Число и цифра 5  Роль и место математики в современном мире. Пределы. Свойства пределов. Тема 1.1
Роль и место математики в современном мире. Пределы. Свойства пределов. Тема 1.1 Презентация на тему Решение некоторых иррациональных уравнений
Презентация на тему Решение некоторых иррациональных уравнений  Интегральное исчисление. Первообразная функция. Неопределённый интеграл
Интегральное исчисление. Первообразная функция. Неопределённый интеграл Презентация на тему Умножение и деление на 10
Презентация на тему Умножение и деление на 10 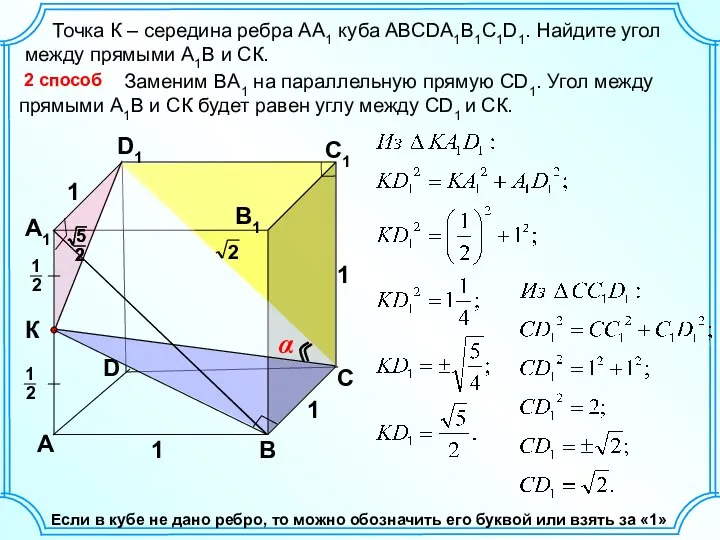 Решение задач
Решение задач Презентация на тему Виды вкладов и расчет накоплений
Презентация на тему Виды вкладов и расчет накоплений  Обыкновенные дроби. 5 класс
Обыкновенные дроби. 5 класс Первообразная. Таблица для нахождения первообразных элементарных функций
Первообразная. Таблица для нахождения первообразных элементарных функций Основные теоремы теории вероятностей. Лекция 3
Основные теоремы теории вероятностей. Лекция 3 Случаи вычитания 18 -
Случаи вычитания 18 - Дифференциальные и разностные уравнения
Дифференциальные и разностные уравнения Тригонометрия. Графики
Тригонометрия. Графики КВН Знакомьтесь: геометрия
КВН Знакомьтесь: геометрия Экстремум функции с единственной критической точкой
Экстремум функции с единственной критической точкой Функция распределения дискретной случайной величины
Функция распределения дискретной случайной величины Возрастание и убывание функции
Возрастание и убывание функции Мир отрицательных чисел
Мир отрицательных чисел