Занимательная математика. Числовая окружность

Числовая окружность

Числовая окружность.
Числовая окружность в жизни.
Рассмотрим конкретный пример.
Бегун бежит по кругу длиной 400 метров. Спортсмен стартует в точке А (рис. 1) и движется против часовой стрелки. Где он будет находится через 200м, 800м, 1500м.? А где провести финишную черту если бегуну пробежать 4195м.?
Рисунок 1.
Через 200м. бегун будет находиться в точке С, так как он пробежит ровно половину дистанции.
Пробежав 800м., бегун сделает ровно два круга и окажется в точке А.
1500м. это 3 круга по 400 м (1200м.) и еще 300 метров, то есть ¾ от беговой дорожки, финиш этой дистанции в точке D.
Где будет находиться наш бегун пробежав 4195м.? 10 кругов это 4000 метров, останется пробежать 195 метров, это на 5 метров меньше чем половина дистанции. Значит финиш будет в точки М, расположенной около точки С.
Решение:

Числовая окружность.
Определение.
Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам.
Единичной окружностью называют окружность радиуса 1.

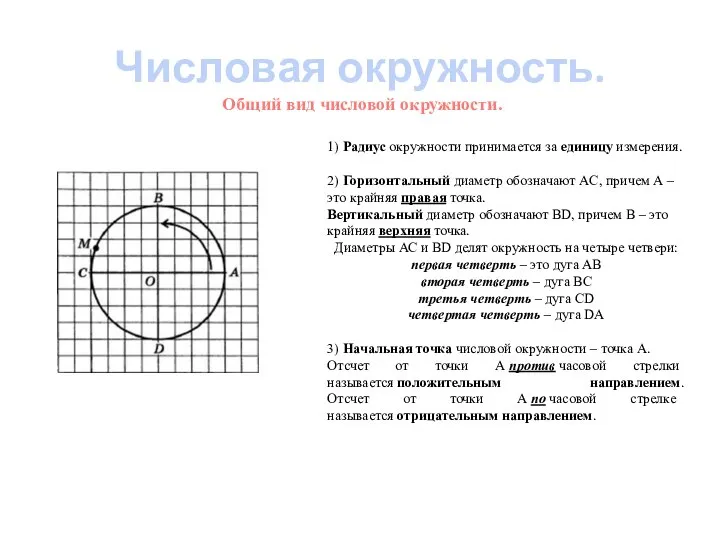
Числовая окружность.
Общий вид числовой окружности.
1) Радиус окружности принимается за единицу измерения.
2) Горизонтальный диаметр обозначают AC, причем А – это крайняя правая точка.
Вертикальный диаметр обозначают BD, причем B – это крайняя верхняя точка.
Диаметры АС и BD делят окружность на четыре четвери:
первая четверть – это дуга AB
вторая четверть – дуга BC
третья четверть – дуга CD
четвертая четверть – дуга DA
3) Начальная точка числовой окружности – точка А.
Отсчет от точки А против часовой стрелки называется положительным направлением.
Отсчет от точки А по часовой стрелке называется отрицательным направлением.

Числовая окружность.
Длина числовой окружности.
Длина числовой окружности вычисляется по формуле:
Так как единичная окружность то
Если взять
то длина окружности
может быть выражена числом

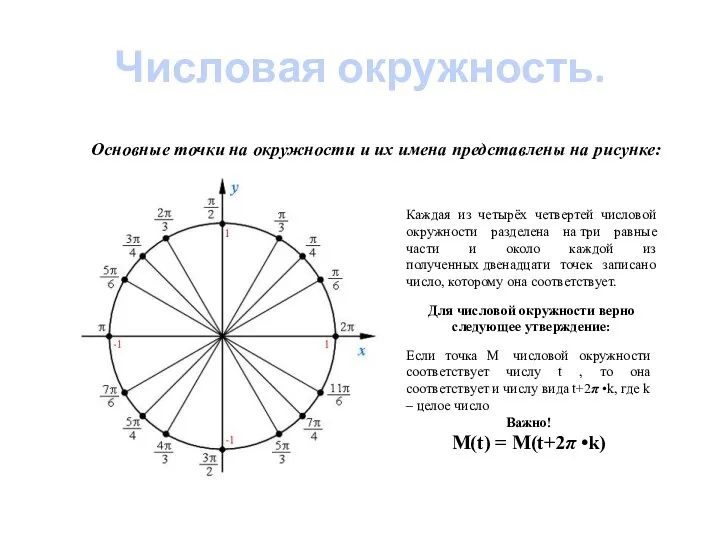
Числовая окружность.
Основные точки на окружности и их имена представлены на рисунке:
Каждая из четырёх четвертей числовой окружности разделена на три равные части и около каждой из полученных двенадцати точек записано число, которому она соответствует.
Для числовой окружности верно следующее утверждение:
Если точка М числовой окружности соответствует числу t , то она соответствует и числу вида t+2π •k, где k – целое число
Важно!
М(t) = M(t+2π •k)

Числовая окружность.
Пример
В единичной окружности дуга АВ разделена точкой М на две равные части, а точками К и Р — на три равные части.
Чему равна длина дуги: AM, МВ, АК, КР, РB, АР, КМ?
Длина дуги АВ = π/2, разделив ее на две равные части точкой М, получим две дуги, длиной — π/4 каждая. Значит, AM = МВ = π/4
Дуга АВ разбита на три равные части точками К и Р, то длина каждой полученной части равна 1/3 · π/2, т. е. π/6 значит, АК = КР = РВ = π/6.
Дуга АР состоит из двух дуг АК и КР длиной — π/6. Значит, АР = 2 • π/6 = π/3
Осталось вычислить длину дуги КМ. Эта дуга получается из дуги AM исключением дуги АК. Таким образом, КМ = AM – АК = π/4 - π/6 = π/12

Числовая окружность.
Пример
Найти на числовой окружности точку которая соответствует заданному числу: 2π , 7π/2 , π/4 , -3π/2.
Решение:
Числу 2π соответствует точка А, т.к. пройдя по окружности путь длиной 2π, т.е. ровно одну окружность, мы опять попадем в точку А
Числу 7π/2 соответствует точка D, т.к. 7π/2 = 2π +3π/2, т.е. двигаясь в положительном направлении, нужно пройти целую окружность и дополнительно путь длиной 3π/2, который закончится в точке D
Числу π/4 соответствует точка М, т.к. двигаясь в положительном направлении, нужно пройти путь в половину дуги АВ длиной π/2, который закончится в точке M.
Числу -3π/2 соответствует точка В, т.к. двигаясь в отрицательном направлении из точки А, нужно пройти путь длиной 3π/2, который закончится в точке В

Числовая окружность.
Пример
Найти на числовой окружности точки а) 21π/4 б) -37π/6
Решение: Пользуясь формулой что число М(t) = M(t+2π •k) (8 слайд) получим
а) 21π/4 = (4+5/4)•π = 4π + 5π/4 = 2 • 2π + 5π/4, значит числу 21π/4 соответствует такое же число что и числу 5/4π - середина третьей четверти.
б) -37π/6 = -(6+1/6)•π = -(6π + π/6) = -3 • 2π - π /6, значит числу -37π/6 соответствует такое же число что и числу - 1/6π, тоже самое что и 11π /6.

Числовая окружность.
Числовая окружность в жизни.
В реальной жизни часто встречается движение по окружности. Например в спорте: соревнования велосипедистов, которые проезжают определенный круг на время или соревнования гоночных автомобилей которым надо проехать наибольшее количество кругов за отведенное время.

Задачи из тригонометрии входят ли ОГЭ, ЕГЭ? Если входят то,
под каким номером в контрольно-измерительных материалах.
2. Какие профессии связаны с числовой окружностью?
Ответ:
Рефлексия:
Чему вы научились на этом уроке …….
Какие задания больше всего трудно решать ……..
Мне бы хотелось на следующем уроке ………….