Содержание
- 2. - раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным
- 3. Комбинаторные задачи.
- 4. КОМБИНАТОРНАЯ ЗАДАЧА – это задача, требующая осуществления перебора всех возможных вариантов или подсчета их числа.
- 5. Термин «комбинаторика» был введён в математический обиход немецким философом, математиком Лейбницем, который в 1666 году опубликовал
- 6. Способы решения комбинаторных задач Перебор вариантов Дерево возможных вариантов По правилу умножения Чтобы процесс перебора возможных
- 7. У Ирины 5 подруг: Вера, Зоя, Марина, Полина и Светлана. Она решила двух из них пригласить
- 8. Составим сначала все пары, в которые входит Вера. ВЗ, ВМ, ВП, ВС Выпишем теперь пары, в
- 9. Задача 2. Буратино пришел в школу и встретил своих друзей Артемона, Пьеро, Мальвину. Они все обменялись
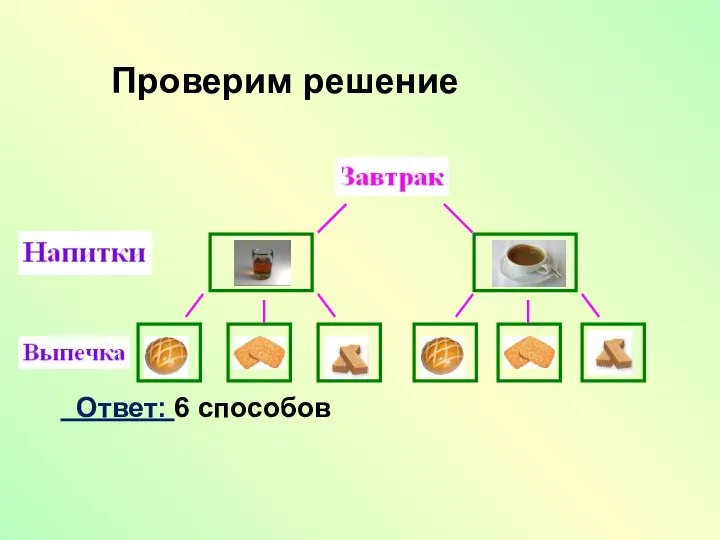
- 10. №4 Сколько различных завтраков, состоящих из 1 напитка и 1 вида выпечки, можно составить из чая,
- 11. Проверим решение Ответ: 6 способов
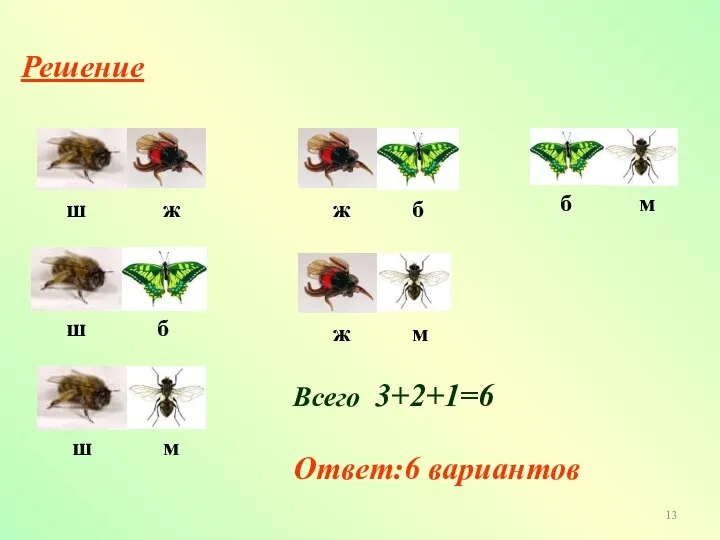
- 12. Рассмотрим еще одну задачу. На цветочной клумбе сидели шмель, жук, бабочка и муха. Два насекомых улетели.
- 13. Решение Всего 3+2+1=6 Ответ:6 вариантов ш ш ш ж ж б б б ж м м
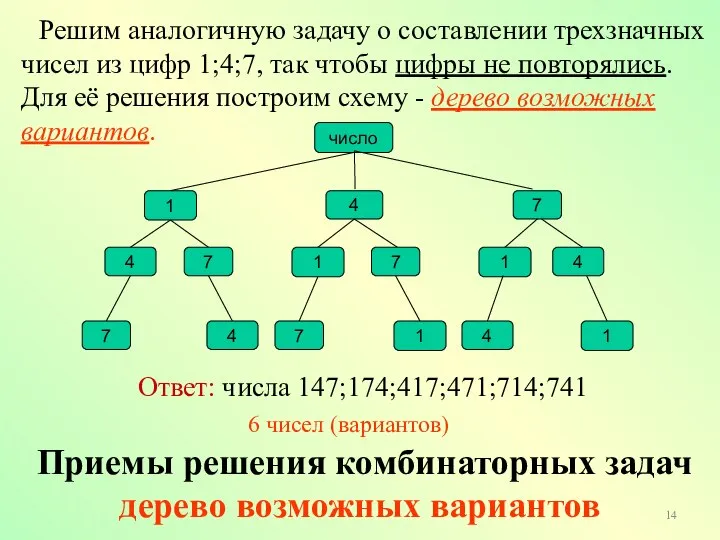
- 14. Приемы решения комбинаторных задач дерево возможных вариантов Решим аналогичную задачу о составлении трехзначных чисел из цифр
- 15. Заметим, что ответ на вопрос, можно получить, не выписывая сами числа. Будем рассуждать так. Первую цифру
- 16. У Куклы Светы 3 юбки и 5 кофт, удачно сочетающихся по цвету. Сколько различных комбинаций одежды
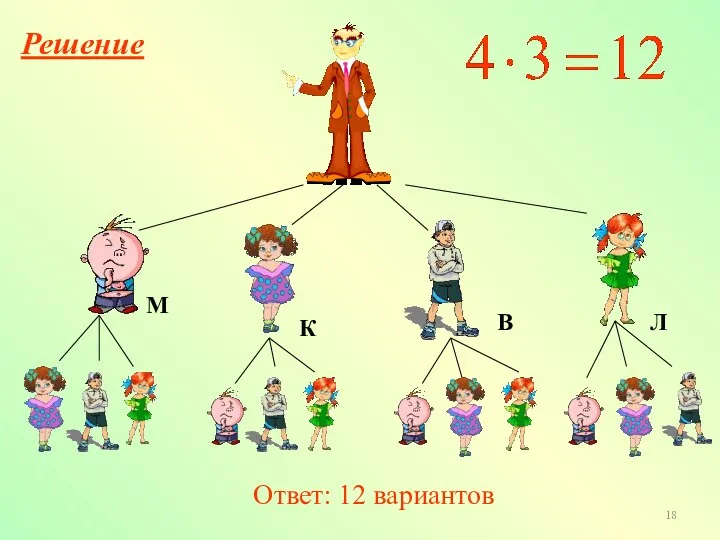
- 17. Решите задачу, используя дерево возможных вариантов и правило умножения В класс пришли четыре новых ученика Миша,
- 18. Ответ: 12 вариантов Решение М В К Л
- 19. Ответим на вопросы: С каким разделом математики вы сегодня познакомились? Какие задачи вы сегодня учились решать?
- 21. Скачать презентацию














 Деление обыкновенных дробей
Деление обыкновенных дробей Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 3
Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 3 Касательная к окружности. 8 класс
Касательная к окружности. 8 класс Путь и перемещение
Путь и перемещение Презентация на тему Умножение десятичных дробей на натуральные числа
Презентация на тему Умножение десятичных дробей на натуральные числа  Деление суммы на число
Деление суммы на число Обобщение. Высказывания. Ориентирование на местности
Обобщение. Высказывания. Ориентирование на местности Интерактивная игра для детей дошкольного возраста Путешествие в страну Математика
Интерактивная игра для детей дошкольного возраста Путешествие в страну Математика Подготовка к блиц-турниру
Подготовка к блиц-турниру Таблицы умножения и деления на 2 и 3
Таблицы умножения и деления на 2 и 3 Множення десяткових дробів. 5 клас
Множення десяткових дробів. 5 клас Степенная функция и её график
Степенная функция и её график Многогранники. Розв'язування задач
Многогранники. Розв'язування задач Обыкновенные дифференциальные уравнения. Вариант 4
Обыкновенные дифференциальные уравнения. Вариант 4 Решение уравнений (урок 3). 6 класс
Решение уравнений (урок 3). 6 класс Понятия и свойства функции. Предел функции
Понятия и свойства функции. Предел функции Число 0. Цифра 0
Число 0. Цифра 0 Предмет стереометрии. Аксиомы стереометрии
Предмет стереометрии. Аксиомы стереометрии Теорема Пифагора
Теорема Пифагора Презентация на тему Изображение пространственных фигур
Презентация на тему Изображение пространственных фигур 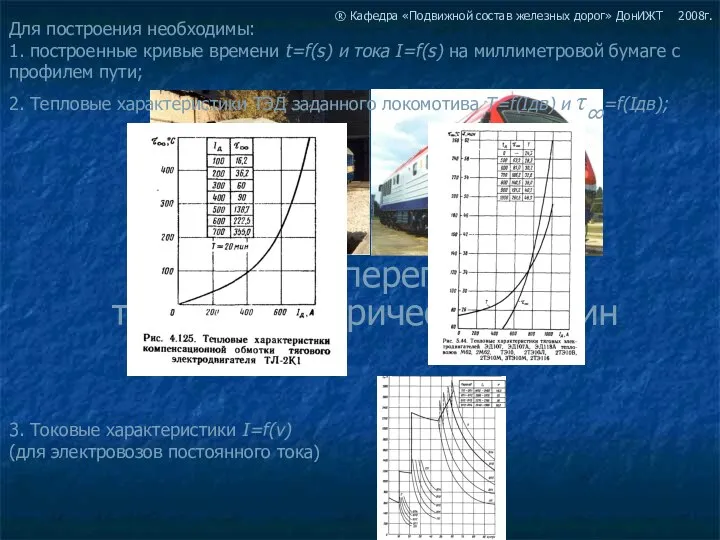 Расчет перегрева тяговых электрических машин
Расчет перегрева тяговых электрических машин Степенные функции, их свойства и графики
Степенные функции, их свойства и графики Введение в фармакологию
Введение в фармакологию Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Функции и их графики
Функции и их графики Производная произведения. Производная частного
Производная произведения. Производная частного Сечение куба, призмы, пирамиды
Сечение куба, призмы, пирамиды Параллельный перенос и поворот
Параллельный перенос и поворот