- Главная
- Математика
- Режим поступления заявок

Содержание
- 2. Режим поступления заявок Режим поступления заявок: По определенному графику (например, каждые 15-20 минут) Случайным образом (появления
- 3. По определенному графику Рассмотрим на примере маникюрного салона. Например, клиент приходит к мастеру по записи каждые
- 4. Случайный режим поступления Случайные заявки могут появляться, например, на пунктах оплаты на скоростных дорогах. Мы не
- 5. Часто в задачах массового обслуживания число появлений в единицу времени может быть оценено с помощью распределения
- 6. Большинство моделей очередей основывается на предположении, что поведение клиентов является стандартным, т. е. каждая поступающая в
- 7. Таким образом, можно сделать вывод, что за 2 минуты на станцию не придет ни одного вызова
- 9. Скачать презентацию
Слайд 2Режим поступления заявок
Режим поступления заявок:
По определенному графику (например, каждые 15-20 минут)
Случайным образом
Режим поступления заявок
Режим поступления заявок:
По определенному графику (например, каждые 15-20 минут)
Случайным образом

Заявка (запрос, требование, вызов, клиент, сообщение, пакет) — объект, поступающий в СМО и требующий обслуживания в приборе. Совокупность последовательных заявок, распределенных во времени, образуют входной поток заявок.
Слайд 3По определенному графику
Рассмотрим на примере маникюрного салона. Например, клиент приходит к мастеру
По определенному графику
Рассмотрим на примере маникюрного салона. Например, клиент приходит к мастеру

Слайд 4Случайный режим поступления
Случайные заявки могут появляться, например, на пунктах оплаты на скоростных
Случайный режим поступления
Случайные заявки могут появляться, например, на пунктах оплаты на скоростных

Еще одним примером случайного появления заявки на входе в СМО выступает супермаркет, мы не можем сказать точно сколько клиентов посетит супермаркет в определенный час.
Слайд 5Часто в задачах массового обслуживания число появлений в единицу времени может быть
Часто в задачах массового обслуживания число появлений в единицу времени может быть

где р(х) — вероятность поступления х заявок в единицу времени;
х —число заявок в единицу времени;
λ— среднее число заявок в единицу времени (темп поступления заявок);
е = 2,7183 (основание натурального логарифма).
Соответствующие значения вероятностей р(х) нетрудно определить с помощью таблицы пуассоновского распределения. На практике вероятности появления заявок, разумеется, не всегда подчиняются пуассоновскому распределению (они могут иметь какое-то другое распределение). Поэтому требуется проводить предварительные исследования для того, чтобы проверить, что пуассоновское распределение может служить хорошей аппроксимацией.
(1.1)
Слайд 6Большинство моделей очередей основывается на предположении, что поведение клиентов является стандартным, т.
Большинство моделей очередей основывается на предположении, что поведение клиентов является стандартным, т.

Жизнь значительно сложнее. На практике клиенты могут покинуть очередь потому, что она оказалась слишком длинной. Может возникнуть и другая ситуация: клиенты дожидаются своей очереди, но по каким-то причинам уходят необслуженными. Эти случаи также являются предметом теории
массового обслуживания, однако здесь не рассматриваются.
Поведение клиентов
Слайд 7Таким образом, можно сделать вывод, что за 2 минуты на станцию не
Таким образом, можно сделать вывод, что за 2 минуты на станцию не

Пример решения задачи
ДАНО. На станцию поступает простейший поток вызовов с интенсивностью λ=1,2 вызовов в минуту. Найти вероятность того, что за две минуты: а) не придет ни одного вызова;
б) придет ровно один вызов;
в) придет хотя бы один вызов.
РЕШЕНИЕ.
а) Случайная величина X – число вызовов за две минуты – распределена по закону Пуассона с параметром λt=1,2·2=2,4 Вероятность того, что вызовов не будет (х = 0), по формуле: P(t) = e^(−λt):
P0(2) ≈ e^(−2,4) ≈ 0,091.
б) Вероятность одного вызова (х =1) по формуле (1.1):
P1(2) ≈ 2,4·0,091 ≈ 0,218
в) Вероятность хотя бы одного вызова:
P(x ≥1) = 1− P(x = 0) = 1− P0(2) ≈ 1− 0,091 = 0,909.
 Пирамиды
Пирамиды Сумма углов геометрических фигур. Транспортир
Сумма углов геометрических фигур. Транспортир Вводная лекция. Урок 1
Вводная лекция. Урок 1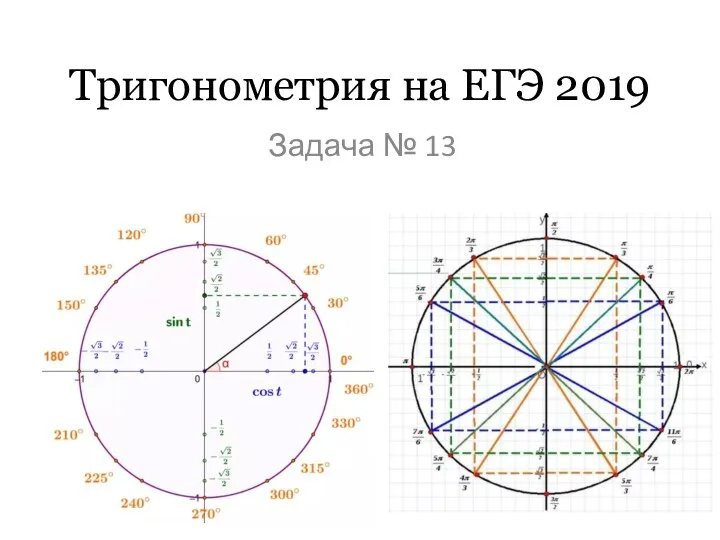 Тригонометрия на ЕГЭ 2019. Задача № 13
Тригонометрия на ЕГЭ 2019. Задача № 13 Письмо цифр
Письмо цифр Задачи на применение формул работы, стоимости, пути
Задачи на применение формул работы, стоимости, пути Бинарный урок физики и геометрии
Бинарный урок физики и геометрии Геометрия. Что значит это слово? часть 1
Геометрия. Что значит это слово? часть 1 Степенная функция
Степенная функция Методика изучения площади
Методика изучения площади Связность графов. Глава 2
Связность графов. Глава 2 Графики
Графики Групповое задание
Групповое задание Устный счёт
Устный счёт Проектирование разноритмичных и неритмичных потоков
Проектирование разноритмичных и неритмичных потоков Повторение пройденного (1 класс)
Повторение пройденного (1 класс) Дифференциальное исчисление функции одной переменной
Дифференциальное исчисление функции одной переменной Аксиомы стереометрии и их простейшие следствия
Аксиомы стереометрии и их простейшие следствия Презентация на тему Страна отрицательных чисел
Презентация на тему Страна отрицательных чисел  Математическая логика и теория алгоритмов
Математическая логика и теория алгоритмов Решение задач. Штрих Шеффера
Решение задач. Штрих Шеффера Дроби вокруг нас. 2 класс
Дроби вокруг нас. 2 класс Решение систем линейных уравнений при помощи компьютерных технологий
Решение систем линейных уравнений при помощи компьютерных технологий Статистические величины и показатели. Тема 4
Статистические величины и показатели. Тема 4 Контрольная работа по алгебре
Контрольная работа по алгебре Логарифмы. Задания В7, В11 на ЕГЭ
Логарифмы. Задания В7, В11 на ЕГЭ Преобразование целого выражения в многочлен
Преобразование целого выражения в многочлен Решение задач составлением систем уравнений с двумя переменными
Решение задач составлением систем уравнений с двумя переменными