Линейные дифференциальные уравнения первого порядка

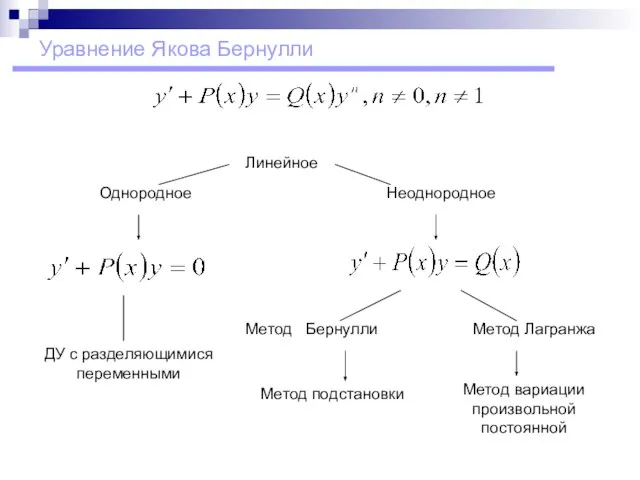
Уравнение Якова Бернулли
Метод Лагранжа
ДУ с разделяющимися переменными
Неоднородное
Однородное
Метод Бернулли
Метод вариации произвольной постоянной
Метод подстановки
Линейное

Линейные дифференциальные уравнения первого порядка
Линейное ДУ первого порядка называется однородным, если функция
Замечание. Уравнение называется линейным, так как искомая функция y и её производная y’ входят в это уравнение в первой степени.
Уравнение вида ,
– функции постоянные величины, называется линейным дифференциальным уравнением первого порядка
Линейное ДУ первого порядка называется неоднородным, если функция

Линейное однородное ДУ первого порядка
1. Решить уравнение
Решение:
имеем
Получаем
(общее решение)
2. Решить уравнение
Выразить производную функции через дифференциалы
Разделить переменные
Интегрировать
(общее решение)
Решение:

Линейное неоднородное ДУ. Метод Бернулли
Замечание. Любую величину можно представить в форме произведения двух сомножителей, причем один из множителей можно выбрать по своему желанию.
В результате линейное неоднородное ДУ сводиться к двум уравнениям с разделяющимися переменными.
где
и
- новые функции переменной
1. Решить уравнение
Решение:
Положим
тогда

Алгоритм решения линейного ДУ первого порядка
1. Приводят уравнение к виду
находят
2. Используя подстановку
и подставляют эти выражения в уравнение.
3. Группируют члены уравнения, выносят одну из функций
за скобки. Находят вторую функцию, приравняв выражение в скобках нулю и решив полученное уравнение.
4. Подставляют найденную функцию в оставшееся выражение и находят вторую функцию.
5. Записывают общее решение, подставив выражения для найденных функций и в равенство
6. Если требуется найти частное решение , то определяют С из начальных условий и подставляют в общее решение.
или

Получим
или
Выразить производную функции через дифференциалы
Разделить переменные
Интегрировать
С=0, ввиду произвольности в выборе
(1)
Имеем
ЗП

Выразить производную функции через дифференциалы
Разделить переменные
Интегрировать
постоянную С писать обязательно!
Окончательно получим
(общее решение)
Замечание. Уравнение (1) можно было записать в эквивалентном виде:
=0
Находим u из ур-ния, приравняв выражение в скобках к нулю. Затем, находим V , решая уравнение u v =x