Содержание
- 2. Ричард Олдингтон (1892 – 1962гг..) - английский поэт, прозаик, критик «Ничему тому, что важно знать, научить
- 3. Уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании, называется логарифмическим уравнением. Решение логарифмических
- 4. Проверка: Ответ: 4. Пример 3: Ответ: Пример 2:
- 5. Пример 4: ОДЗ: Ответ: 2.
- 6. 2. Метод потенцирования. Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их.
- 7. Пример 6: Проверка: верно. не верно Ответ: 1. ОДЗ:
- 8. Пример 7: получим Проверка: Ответ: 0. верно
- 9. 3. Метод подстановки. Пример 8: Ответ: ОДЗ: Пусть тогда Значит, или
- 10. Пример 9: Ответ: ОДЗ: Приведём логарифмы к одному основанию – 7: Подстановка: Уравнение примет вид: Значит,
- 11. 4. Метод логарифмирования. Пример 10: Ответ: 3; 27. ОДЗ: Пусть тогда Значит, или
- 12. Выводы: На основании определения логарифма. Метод потенцирования. Метод постановки. Метод логарифмирования.
- 14. Скачать презентацию











 32046
32046 Признак параллельности прямых. Задачи для устной работы
Признак параллельности прямых. Задачи для устной работы Показатели вариации
Показатели вариации Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Геометрические тела. Многогранники
Геометрические тела. Многогранники Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Понятие производной
Понятие производной Tema1_TeoriaMnozhestv
Tema1_TeoriaMnozhestv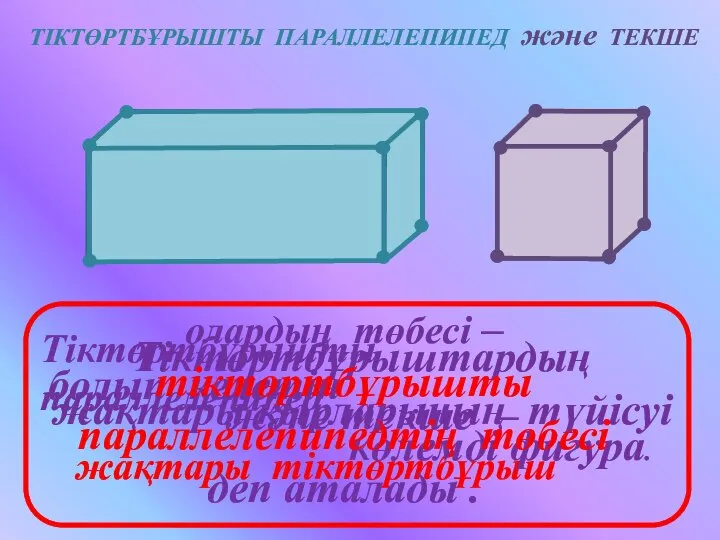 Тіктөртбұрышты параллелепипед және текше
Тіктөртбұрышты параллелепипед және текше Свойства логарифмов
Свойства логарифмов Элементы геометрии на небесной сфере. Лекция 1
Элементы геометрии на небесной сфере. Лекция 1 Признаки параллелограмма
Признаки параллелограмма Найдите все значения параметра a,
Найдите все значения параметра a, аксиомы стереометрии
аксиомы стереометрии Практикум по решению задач практической направленности
Практикум по решению задач практической направленности Умножение дробей
Умножение дробей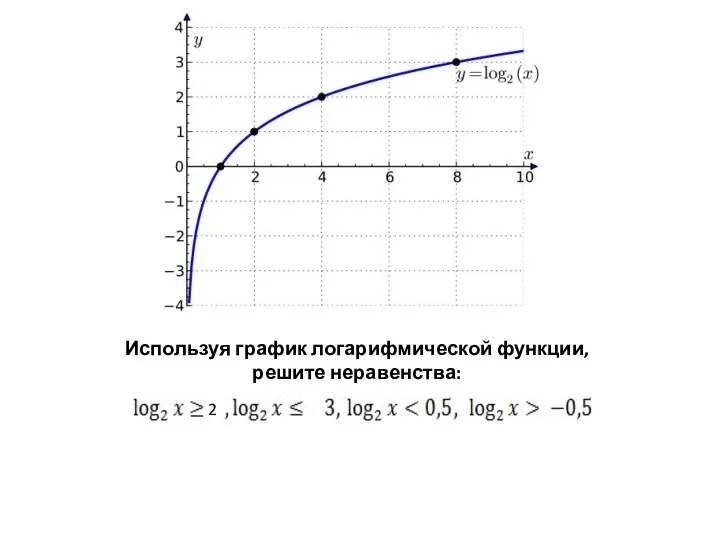 Логарифмические неравенства. устные упражнения
Логарифмические неравенства. устные упражнения Логарифмы. Логарифм числа. Основное логарифмическое тождество. Основные свойства логарифма
Логарифмы. Логарифм числа. Основное логарифмическое тождество. Основные свойства логарифма угол между прямой и плоскостью (1)
угол между прямой и плоскостью (1) Учимся писать цифры
Учимся писать цифры Векторы. Нулевой вектор
Векторы. Нулевой вектор Сравнение дробей. 1 часть
Сравнение дробей. 1 часть Живая планета!
Живая планета! Преобразование иррациональных выражений
Преобразование иррациональных выражений Арифметичская прогрессия
Арифметичская прогрессия Приём вычислений вида 35 - 7. 2 класс
Приём вычислений вида 35 - 7. 2 класс Волшебная страна математики: основы математики для детей 5-6 лет
Волшебная страна математики: основы математики для детей 5-6 лет Косинус острого угла прямоугольного треугольника
Косинус острого угла прямоугольного треугольника