Содержание
- 2. Тема урока: Логарифмы
- 3. В 1590 году шотландский математик Джон НЕПЕР пришел к идее логарифмических вычислений и составил первые таблицы
- 4. Применение логарифма Банковские расчёты География Расчёты в производстве Биология Химия Физика Астрономия Психология Социология Музыка
- 5. Некоторая сумма денег в A руб. подвержена приросту в p% годовых. Через сколько лет эта сумма
- 6. Альпинисты, поднимаясь на пик Победы, достигли высоты, где давление было равно 304 мм рт. ст. Вычислим,
- 7. Увеличение диаметра объектива телескопа позволяет видеть всё большее количество звёзд, не различимых простым глазом. При этом
- 8. Что такое логарифм? Как решать логарифмы? Эти вопросы многих выпускников вводят в ступор. Традиционно тема логарифмов
- 9. 1. Поймете, что такое логарифм. 2. Научитесь решать целый класс показательных уравнений. Даже если ничего о
- 10. Для начала решите в уме вот такое уравнение: 3x = 9 Удалось? Ну да, х =
- 11. Что, что-то не так? 3x = 8 Ответ, что нету такого икса, не принимается! Согласитесь, что
- 12. Вернёмся к нашему загадочному примеру: 3x = 8 х - это число, в которое надо возвести
- 13. назовём это число логарифмом восьми по основанию три. Записывается это вот как: х = log38 Читаем
- 14. Как решить пример: 5x = 12 ? Легко! х - это число, в которое надо возвести
- 15. Ещё пример: 2x =135 Элементарно! х = log2135 И ещё: 19x = 0,352 Не вопрос! х
- 16. Вас смущает, что вместо конкретного числа мы пишем какие-то значки с цифрами? Ну ладно, только для
- 17. Но радость от новых знаний будет неполной без ложки дегтя. Если логарифм считается без калькулятора, его
- 18. log327 = 3 Уловили? Ну-ка разовьём успех! Решаем примеры: log381 = 2 1 3 4 5
- 19. log327 = 3 Уловили? Ну-ка разовьём успех! Решаем примеры: log381 = log55 = 4 2 1
- 20. log327 = 3 Уловили? Ну-ка разовьём успех! Решаем примеры: log381 = log416 = log55 = 1
- 21. log327 = 3 Уловили? Ну-ка разовьём успех! Решаем примеры: log381 = log416 = log55 = log6216
- 22. log327 = 3 Уловили? Ну-ка разовьём успех! Решаем примеры: log381 = log416 = log55 = log6216
- 23. Вот мы и познакомились с логарифмами. На понятном уровне. Вы убедились, что они не опасны. Но
- 24. Прикинем, любым ли числом может быть а? Если, к примеру, а = 1? Забавно получится, единица
- 25. Ещё не мешает знать, что такое десятичный логарифм и что такое натуральный логарифм? В математике два
- 27. Скачать презентацию



















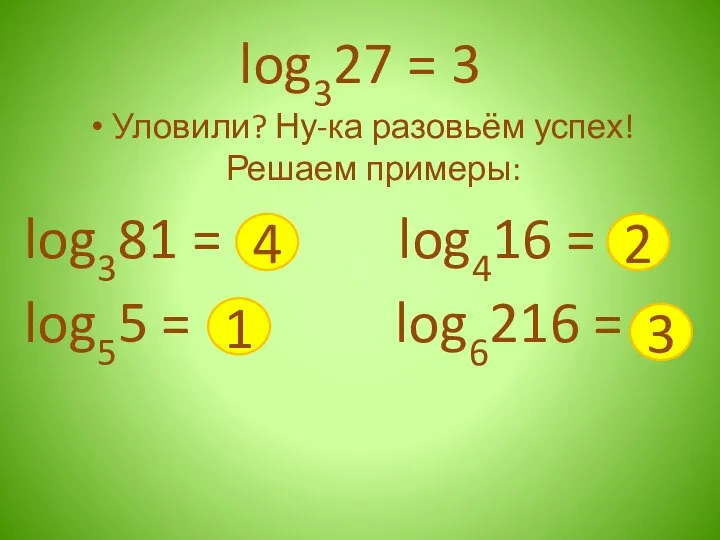



 3.2 Численные методы решения систем линейных алгебраических уравнений
3.2 Численные методы решения систем линейных алгебраических уравнений Аксиомы стереометрии. Взаимное расположение прямых и плоскостей в пространстве
Аксиомы стереометрии. Взаимное расположение прямых и плоскостей в пространстве Симметрия 11кл
Симметрия 11кл Первый признак подобия треугольников. 8 класс
Первый признак подобия треугольников. 8 класс Следствия из аксиом I - III
Следствия из аксиом I - III Метод Гаусса для решения систем линейных уравнений
Метод Гаусса для решения систем линейных уравнений Презентация на тему Перпендикулярность прямой и плоскости
Презентация на тему Перпендикулярность прямой и плоскости  Прогрессия. Анзац
Прогрессия. Анзац Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Прямые на плоскости. Задачи 6 и 7
Прямые на плоскости. Задачи 6 и 7 Состав числа. Тренажер. Старшая группа
Состав числа. Тренажер. Старшая группа Введение в дисциплину Математические модели в экологических системах
Введение в дисциплину Математические модели в экологических системах Касательная к окружности. Свойства касательных к окружности
Касательная к окружности. Свойства касательных к окружности Построения в пространстве
Построения в пространстве Прямоугольный параллелепипед
Прямоугольный параллелепипед Тригонометриялық теңдеулерді шешу тәсілдерін үйрену
Тригонометриялық теңдеулерді шешу тәсілдерін үйрену Единицы измерения. Килограмм. Грамм
Единицы измерения. Килограмм. Грамм Площадь и периметр ромба
Площадь и периметр ромба Великий квадрат не знает пределов
Великий квадрат не знает пределов Матрицы. Действия над матрицами
Матрицы. Действия над матрицами Математика для дошкольников (средняя группа)
Математика для дошкольников (средняя группа) Решение задач на нахождение неизвестного вычитаемого
Решение задач на нахождение неизвестного вычитаемого Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Треугольники. Задача
Треугольники. Задача Фигуры. Геометрия
Фигуры. Геометрия С чего начать подготовку к ЕГЭ по профильной математике
С чего начать подготовку к ЕГЭ по профильной математике Деление одночлена на одночлен. 7 класс. Урок 49
Деление одночлена на одночлен. 7 класс. Урок 49 Кривые Безье
Кривые Безье