Содержание
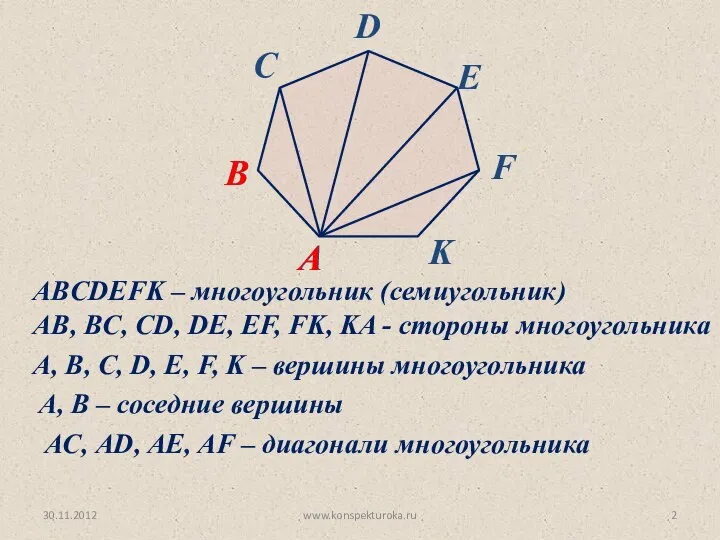
- 2. 30.11.2012 www.konspekturoka.ru ABCDEFK – многоугольник (семиугольник) AB, BC, CD, DE, EF, FK, KA - стороны многоугольника
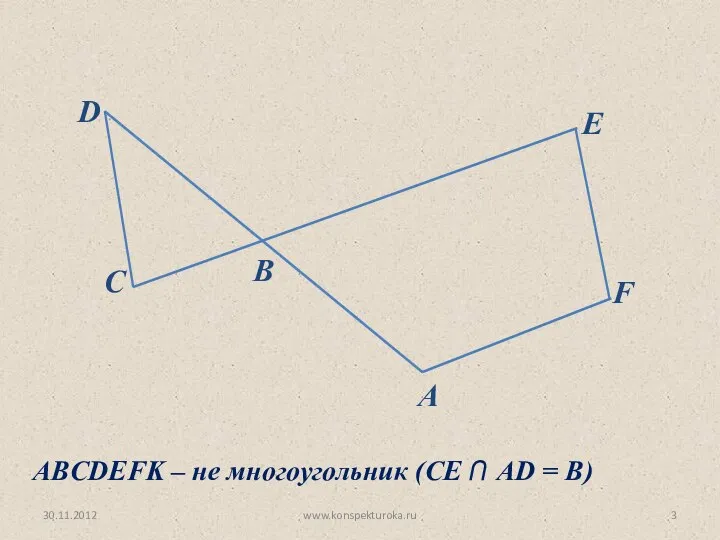
- 3. 30.11.2012 www.konspekturoka.ru C D B E F A ABCDEFK – не многоугольник (СЕ ⋂ AD =
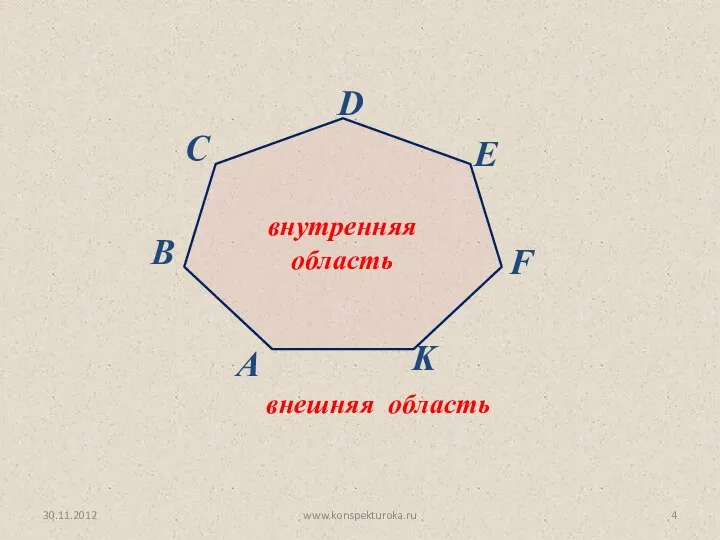
- 4. 30.11.2012 www.konspekturoka.ru внутренняя область внешняя область
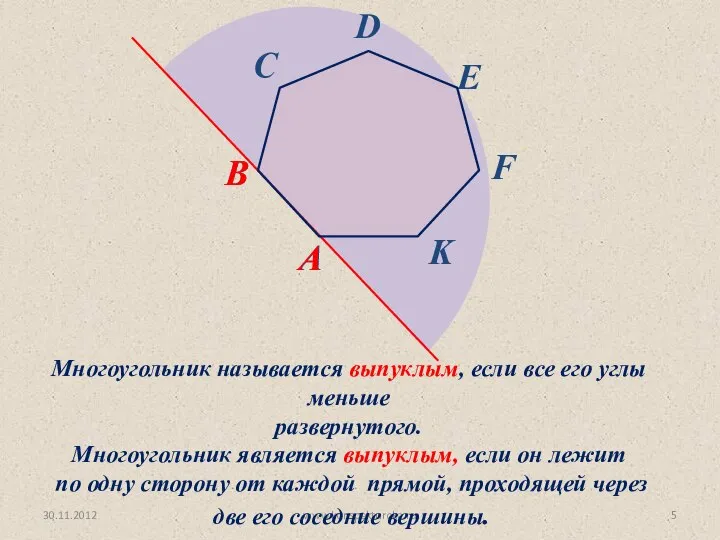
- 5. 30.11.2012 www.konspekturoka.ru Многоугольник называется выпуклым, если все его углы меньше развернутого. Многоугольник является выпуклым, если он
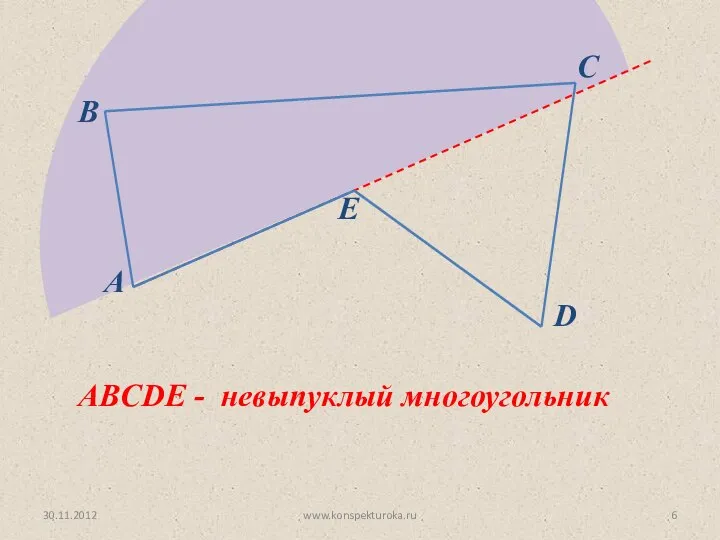
- 6. 30.11.2012 www.konspekturoka.ru A B E C D ABCDE - невыпуклый многоугольник
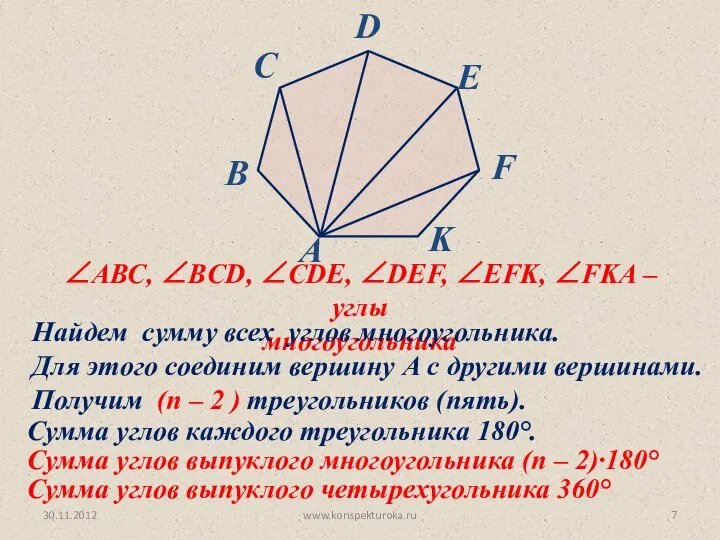
- 7. 30.11.2012 www.konspekturoka.ru ∠AВС, ∠BCD, ∠CDE, ∠DEF, ∠EFK, ∠FKA – углы многоугольника Найдем сумму всех углов многоугольника.
- 9. Скачать презентацию
 Единицы массы 4 класс - презентация_
Единицы массы 4 класс - презентация_ Деление с остатком. Решение задач
Деление с остатком. Решение задач Уточнение параметров в ксеноновых процессах в реакторах типа ВВЭР-1000 при помощи экспериментальных данных
Уточнение параметров в ксеноновых процессах в реакторах типа ВВЭР-1000 при помощи экспериментальных данных Окружность. 7 класс
Окружность. 7 класс Непрерывные функции
Непрерывные функции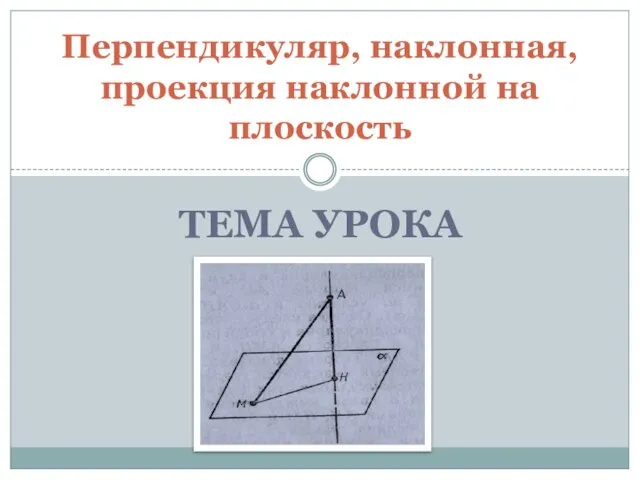 Презентация на тему Перпендикуляр, наклонная, проекция наклонной на плоскость
Презентация на тему Перпендикуляр, наклонная, проекция наклонной на плоскость  Стороны треугольника пропорциональны синусам противолежащих углов
Стороны треугольника пропорциональны синусам противолежащих углов Показательная, степенная и логарифмическая функции их свойства и графики
Показательная, степенная и логарифмическая функции их свойства и графики Кручение
Кручение Лекция. Ряды
Лекция. Ряды Лабораторные работы по геометрическому материалу
Лабораторные работы по геометрическому материалу Презентация на тему Приложения производной
Презентация на тему Приложения производной  Квадратные уравнения
Квадратные уравнения Решение показательных неравенств
Решение показательных неравенств Проекция вектора перемещения
Проекция вектора перемещения Известное и неизвестное
Известное и неизвестное Презентация на тему Решение квадратных неравенств
Презентация на тему Решение квадратных неравенств  Сложение векторов
Сложение векторов В мире треугольников (2). 7 класс
В мире треугольников (2). 7 класс Решение систем уравнений и неравенств графическим способом
Решение систем уравнений и неравенств графическим способом Неисключенные остатки систематической погрешности. Статистическая обработка однократных наблюдений. Случайные погрешности
Неисключенные остатки систематической погрешности. Статистическая обработка однократных наблюдений. Случайные погрешности Презентация на тему Действия с векторами
Презентация на тему Действия с векторами  Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Описанная и вписанная окружности треугольника
Описанная и вписанная окружности треугольника Показательные уравнения
Показательные уравнения Regresní a korelační analýza
Regresní a korelační analýza Комплексные числа и квадратные уравнения
Комплексные числа и квадратные уравнения Методика изучения времени. Время
Методика изучения времени. Время