Содержание
- 2. История дифференциального исчисления История возникновения дифференциального исчисления Дифференциальное исчисление было создано Ньютоном и Лейбницем в конце
- 3. Сэр Исаак Ньютон 04.01.1643 – 31.03.1727 Английский физик, математик и астроном, один из создателей классической физики.
- 4. Сэр Исаак Ньютон Вулсторп. Дом, где родился Ньютон. Тринити-колледж, в котором учился Ньютон. Почитаемый потомок «Яблони
- 5. Готфрид Вильгельм Лейбниц 01.07.1646 – 25.11.1716 Немецкий философ, логик, математик, физик, юрист, историк, дипломат, изобретатель и
- 6. Готфрид Вильгельм Лейбниц Церковь и Школа Святого Фомы Альтдорфский университет Копия механического калькулятора Лейбница Дом Лейбница
- 7. Огюстен Луи Коши 21.08.1789 – 23.05.1857 Великий французский математик, член Парижской академии наук, Лондонского королевского общества,
- 8. Огюстен Луи Коши Политехническая Школа Сорбонна Коллеж де Франс Туринский университет
- 9. Производные и дифференциалы Определение производной Производная и дифференциал. Таблица производных. Необходимое условие дифференцируемости. Геометрический смысл производной.
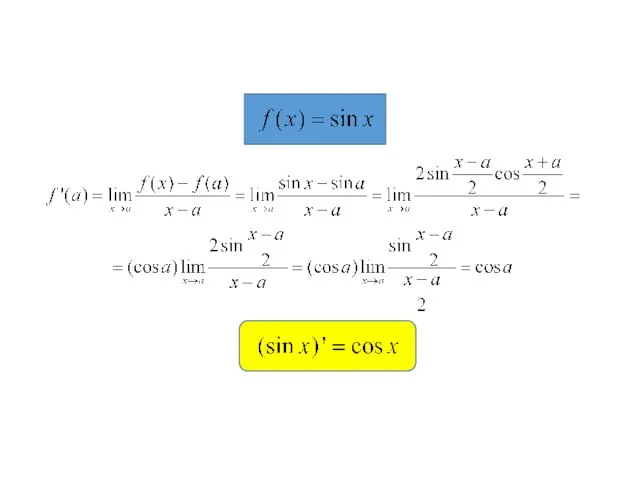
- 10. Производной функции f(x) в точке x=a называют предел отношения приращения функции к приращению аргумента когда аргумент
- 11. С понятием производной тесно связано понятие дифференциала и понятие дифференцируемой функции. Функция f(x) называется дифференцируемой в
- 12. Справедливо следующее утверждение. Теорема. Пусть функция f(x) имеет производную в точке x=a, тогда она дифференцируема в
- 13. Доказательство. Пусть функция имеет производную f'(a) , тогда где α(x) ‒ функция, имеющая при x --->
- 14. Обратно, пусть функция дифференцируема, тогда где α(x) ‒ функция, имеющая при x ---> a предел, равный
- 15. Слагаемое A(x-a) , входящее в определение дифференцируемости, носит название главной линейной частью приращения функции в точке
- 16. Дифференциал На практике обычно принято записывать все формулы, в которые входит производная или дифференциал, не вводя
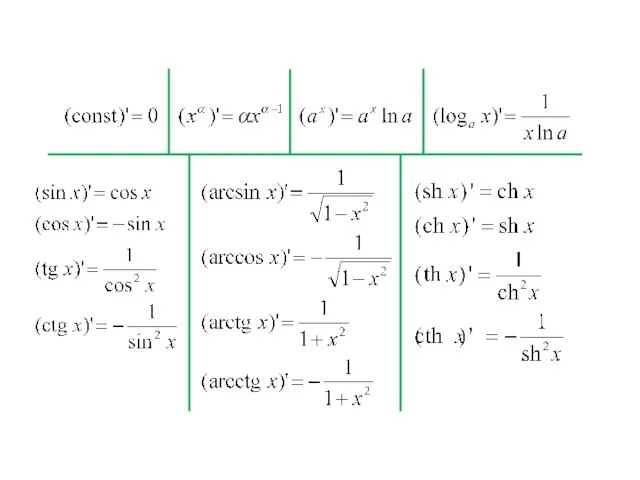
- 17. Таблица производных
- 18. Пример
- 19. Таблица дифференциалов
- 20. Теорема. Если функция дифференцируема, то она непрерывна. Доказательство. Согласно доказанной выше теореме Поэтому Отсюда следует, что
- 21. Обратное утверждение неверно. Непрерывная функция может не иметь производной. В этом можно убедиться на примере функции
- 22. Геометрический смысл производной Если существует предел углового коэффициента секущей AB при x ----> x0, то прямую
- 23. Уравнение прямой, проходящей через заданную точку (x0,y0) и имеющей угловой коэффициент k , имеет вид Отсюда
- 24. Прямая, которая проходит через точку (x0,f(x0)) и перпендикулярна касательной в этой точке, называется нормалью. Известно, что
- 25. Физический смысл производной Пусть материальная точка совершает прямолинейное движение и xx(t) – ее координата, отсчитываемая от
- 26. Основные правила вычисления производных Производная суммы. Производная разности. Производная произведения. Производная частного. Производная сложной функции. Производная
- 27. Производная суммы и разности
- 28. Производная произведения
- 29. Производная частного
- 30. Производная сложной функции Рассмотрим сложную функцию Если существуют производные то ее производная определяется формулой
- 31. Производная сложной функции Доказательство. Функция f(t) дифференцируема в точке поэтому по свойству дифференцируемой функции где α(t)
- 32. где Производная сложной функции
- 33. Так как функция t=φ(x) дифференцируема в точке x = x0 , то она непрерывна в этой
- 34. Итак где и Отсюда следует, что функция дифференцируема в точке и ее производная Производная сложной функции
- 35. Производная обратной функции Пусть функция монотонна и непрерывна в окрестности точки x0 , в самой точке
- 36. Производная обратной функции Доказательство. Из условий теоремы вытекает непрерывность обратной функции, поэтому при y ---> y0
- 37. Производная функции в параметрической форме Рассмотрим функцию заданную в параметрическом виде Пусть функция x=φ(t) непрерывна и
- 38. Производная функции в параметрической форме Доказательство. В самом деле, при тех предположениях, которые сделаны, функция x=φ(t)
- 39. Производная «показательно-степенной» функции Показательно-степенной функцией условно называют функцию вида Производную этой функции можно найти если предварительно
- 40. Основные правила вычисления дифференциалов Дифференциал суммы. Дифференциал разности. Дифференциал произведения. Дифференциал частного. Дифференциал сложной функции.
- 41. Дифференциал суммы Дифференциал разности Дифференциал произведения Дифференциал частного Основные правила вычисления дифференциалов
- 42. Дифференциал сложной функции Полученная формула допускает важную интерпретацию. Формула для дифференциала сложной функции оказывается одинаковой независимо
- 44. Скачать презентацию
























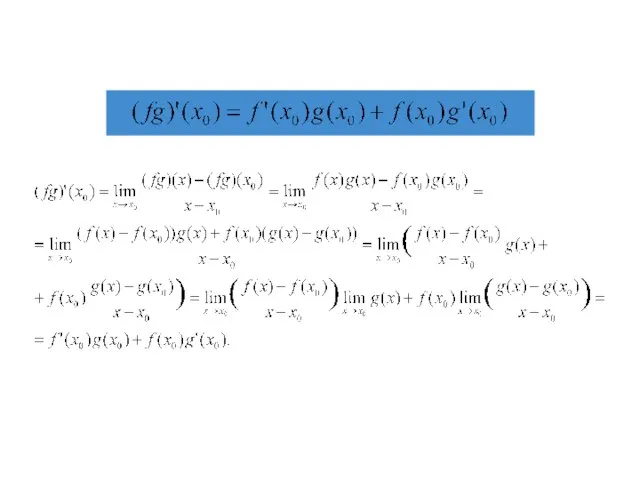



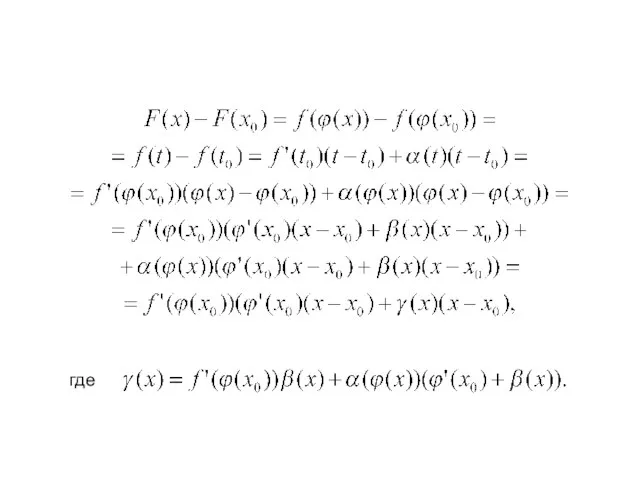










 ЕГЭ 2021. Задания 1-19 (11 класс)
ЕГЭ 2021. Задания 1-19 (11 класс) Математика
Математика Математический анализ
Математический анализ Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс
Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс Модуль. Определение. Свойства. Геометрический смысл модуля
Модуль. Определение. Свойства. Геометрический смысл модуля Теория множеств
Теория множеств Коэффициенты линейных функций
Коэффициенты линейных функций Теорема косинусов для треугольника (задача)
Теорема косинусов для треугольника (задача) Число и цифра 2
Число и цифра 2 Урок-лекция Угол между двумя векторами
Урок-лекция Угол между двумя векторами Сакральная геометрия
Сакральная геометрия Сложение и вычитание числа 2
Сложение и вычитание числа 2 Определение медианы
Определение медианы Графики функций
Графики функций ОГЭ 2020-21. Задание №8
ОГЭ 2020-21. Задание №8 Домашнее задание по теме операторы
Домашнее задание по теме операторы Итоговый тест по школьному курсу Геометрия
Итоговый тест по школьному курсу Геометрия Алгоритм Евклида
Алгоритм Евклида Случайные величины. Классификация ошибок измерений. Абсолютная и относительная погрешность
Случайные величины. Классификация ошибок измерений. Абсолютная и относительная погрешность Проверочная работа на конец первой четверти в 5 классе
Проверочная работа на конец первой четверти в 5 классе Порядок оформления практической работы
Порядок оформления практической работы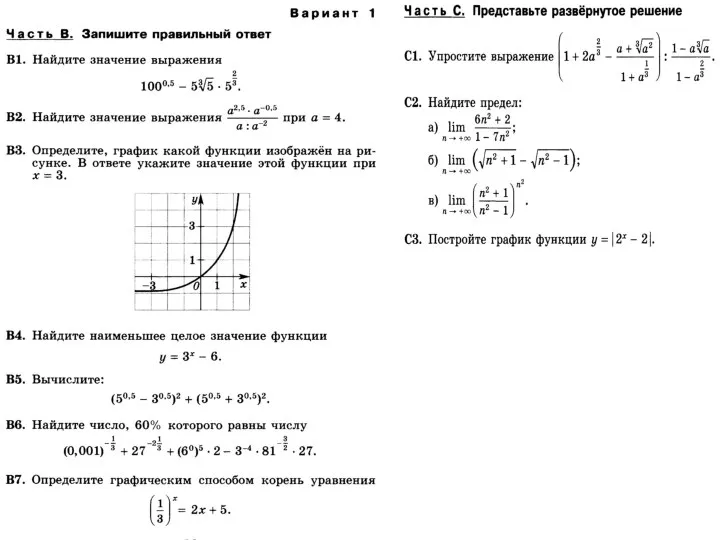 График функции. Тест, 1-6 варианты
График функции. Тест, 1-6 варианты Вычитание. 5 класс
Вычитание. 5 класс Устойчивость движения. Фазовая плоскость. Классификация точек покоя
Устойчивость движения. Фазовая плоскость. Классификация точек покоя Умножение двузначного числа на однозначное. Закрепление. 3 класс
Умножение двузначного числа на однозначное. Закрепление. 3 класс Пересечение линии и поверхности. Позиционные задачи. (Лекция 8.2)
Пересечение линии и поверхности. Позиционные задачи. (Лекция 8.2) Решение уравнений
Решение уравнений Реши уравнения
Реши уравнения