Слайд 2 где коэффициенты А,В,С одновременно не обращаются в нуль. При А =

В = С = 0 уравнение задаёт прямую, которая называется линией первого порядка.
К числу линий второго порядка относятся окружность, эллипс, гипербола и парабола.
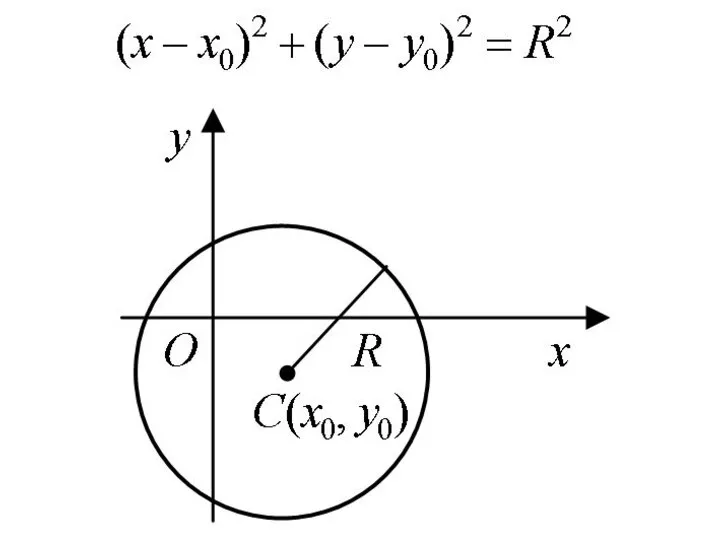
Слайд 3Окружностью называется множество точек плоскости, равноудаленных от данной точки (центра).
Если центр окружности

поместить в начало координат, то каноническое уравнение окружности радиусом R имеет вид
Слайд 4Если центр окружности находится в точке C(x0, y0), то ее уравнение записывается

в виде
Слайд 6Пусть на плоскости заданы две точки F1 и F2, расстояние между которыми

равно 2с, и задано число a > c.
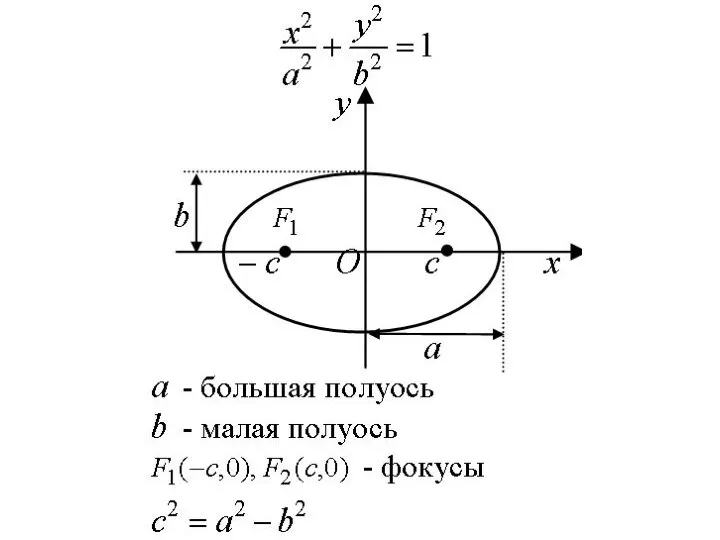
Слайд 7Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных

точек F1 и F2 (фокусов) есть величина постоянная, равная 2а.
Слайд 9Если систему координат выбрать так, как указано на рис., то каноническое уравнение

эллипса запишется в виде
где а – большая, b – малая полуоси эллипса (при a>b).
Слайд 10Фокусы эллипса расположены в точках F1(-c; 0) и F2(c; 0).
Окружность есть

частный случай эллипса при a = b.
Слайд 11Пусть на плоскости заданы две точки F1 и F2, расстояние между которыми

равно 2с, и задано число a < c.
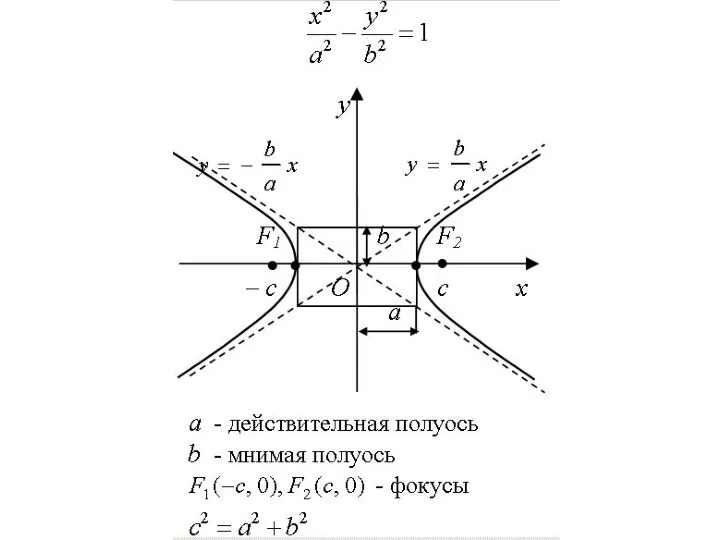
Слайд 12Гиперболой называется множество точек плоскости, модуль разности расстояний от которых до двух

данных точек F1 и F2 (фокусов) есть величина постоянная, равная 2а.
Слайд 14Если систему координат выбрать так, как указано на рис., то каноническое уравнение

гиперболы запишется в виде
где
а – действительная, b – мнимая полуоси гиперболы.
Слайд 15Гипербола состоит из двух ветвей и расположена симметрично относительно координатных осей. При

этом ее ветви при удалении в бесконечность как угодно близко подходят к прямым которые называются асимптотами гиперболы.
Слайд 16При построении гиперболы вначале строят основной прямоугольник со сторонами x = ±

a, y = ± b. Затем через противоположные вершины этого прямоугольника проводят прямые, которые являются асимптотами гиперболы.
Слайд 17Вершины гиперболы расположены в точках с координатами (– а,0) и (а,0), а

фокусы – в точках F1(-c; 0) и F2(c; 0).
Слайд 18Уравнение
(или ) также задаёт гиперболу, сопряженную с гиперболой
Действительная

и мнимая полуоси этой гиперболы соответственно равны b и а.
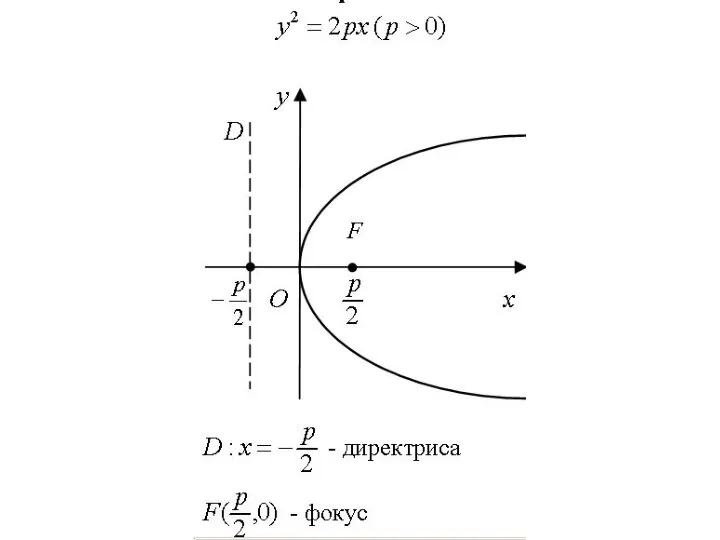
Слайд 19Пусть на плоскости задана точка F и прямая D, расстояние между которыми

равно р.
Параболой называется множество точек плоскости, равноудаленных от данной точки F (фокуса) и данной прямой D (директрисы).
Слайд 21Если систему координат выбрать так, как указано на рис., то каноническое уравнение

параболы запишется в виде
Слайд 22Эта парабола симметрична относительно оси Ох. Директрисой является прямая
точка –

фокус параболы, р – параметр параболы.
Слайд 23Если p < 0, то парабола направлена в противоположную сторону.
Уравнение задаёт

параболу, симметричную относительно оси Оу.
Слайд 24Для того, чтобы построить кривую второго порядка, заданную общим уравнением, уравнение кривой

приводят к каноническому виду и переходят к новой системе координат.
Слайд 25Пример. Определить тип линии и схематически построить её:

Слайд 26Решение. Приведем заданное уравнение к каноническому виду. Для этого в исходном уравнении

выделим полные квадраты по переменным х и у. Перепишем исходное уравнение в виде:
Слайд 30Совершим параллельный перенос координатных осей по формулам:
(2, 3) – координаты

центра O1 системы координат X и Y. В этой системе координат уравнение принимает вид:
Слайд 31Получили каноническое уравнение гиперболы (действительная полуось а = 5, мнимая полуось b

=3)





















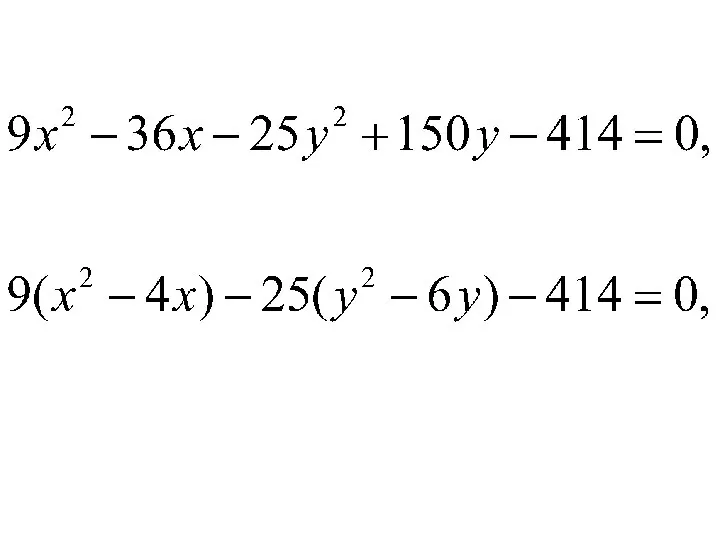
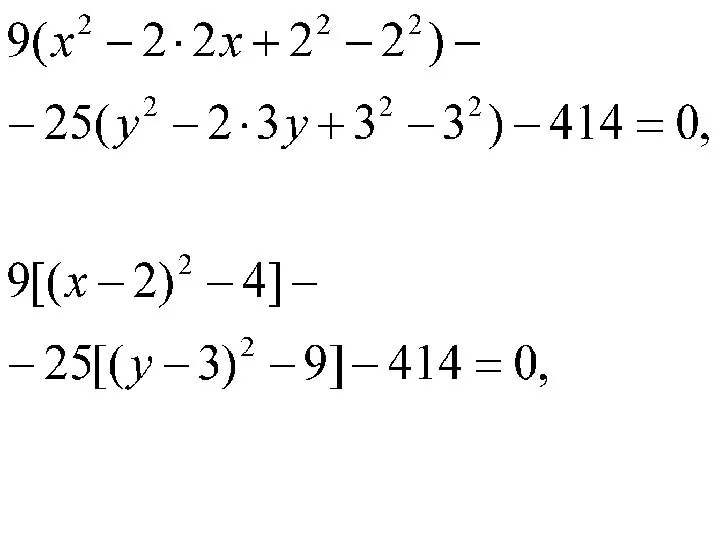
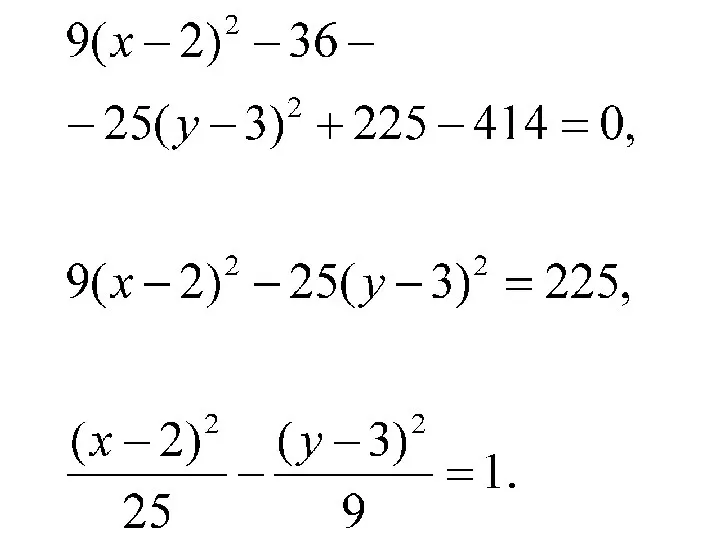


 Признаки параллельности прямых
Признаки параллельности прямых Задача с экологическим содержанием
Задача с экологическим содержанием Разные задачи. Способ Пропорция
Разные задачи. Способ Пропорция Иррациональные уравнения. Открытый урок
Иррациональные уравнения. Открытый урок Необычные способы вычислений
Необычные способы вычислений Путешествие в зазеркалье. Проект по геометрии
Путешествие в зазеркалье. Проект по геометрии Уходя, гасите свет. Математические расчеты
Уходя, гасите свет. Математические расчеты Байесовский анализ и сети Байеса
Байесовский анализ и сети Байеса Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью
Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью Конструирование из счётных палочек
Конструирование из счётных палочек Содержание кривых участков пути. Переходные кривые
Содержание кривых участков пути. Переходные кривые Параллелограмм. Свойства. Признаки
Параллелограмм. Свойства. Признаки В гостях у геометрических фигур
В гостях у геометрических фигур Сложение отрицательных чисел
Сложение отрицательных чисел Квадратичная функция. Наглядно-методическое пособие. 9 класс
Квадратичная функция. Наглядно-методическое пособие. 9 класс Решение задач по теме Правильные многоугольники
Решение задач по теме Правильные многоугольники Дидактические игры в детском саду
Дидактические игры в детском саду Решение задач на вычисление площади поверхности призмы
Решение задач на вычисление площади поверхности призмы Бином Ньютона. Треугольник Паскаля. Решение задач
Бином Ньютона. Треугольник Паскаля. Решение задач Задуманное число. Общий множитель
Задуманное число. Общий множитель Вероятность распределения случайных чисел
Вероятность распределения случайных чисел Конус. Цилиндр. Сфера
Конус. Цилиндр. Сфера Множество значений тригонометрических функций
Множество значений тригонометрических функций Квадратные неравенства
Квадратные неравенства Числа от 1 до 1000, умножение и деление. Приемы устных вычислений
Числа от 1 до 1000, умножение и деление. Приемы устных вычислений Плоскости
Плоскости Решение задач составлением систем уравнений с двумя переменными
Решение задач составлением систем уравнений с двумя переменными Линейные дифференциальные уравнения первого порядка
Линейные дифференциальные уравнения первого порядка