Методический материал по алгебре

Преобразования графиков функций

Оглавление
Правила преобразований графиков функций
Графические иллюстрации
Примеры построения графиков сложных функций с помощью одного преобразования
Примеры построения графиков сложных функций с помощью нескольких преобразований

Построение графика функции y=f(x+a)
Построение графика функции y=f(x)+b
Построение графика функции y=f(-x)
Построение графика функции y=-f(x)
Построение графика функции y=f(kx)
Построение графика функции y=kf(x)
Построение графика функции y=f(|x|)
Построение графика функции y=|f(x)|
оглавление
Правила преобразований
графиков функций

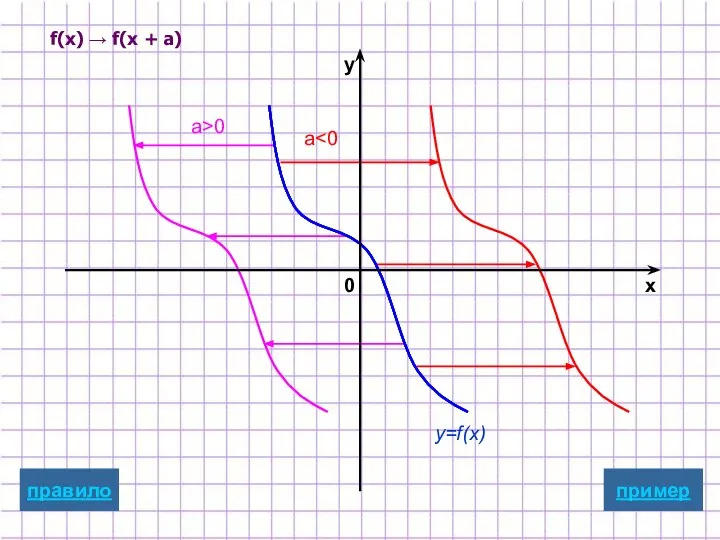
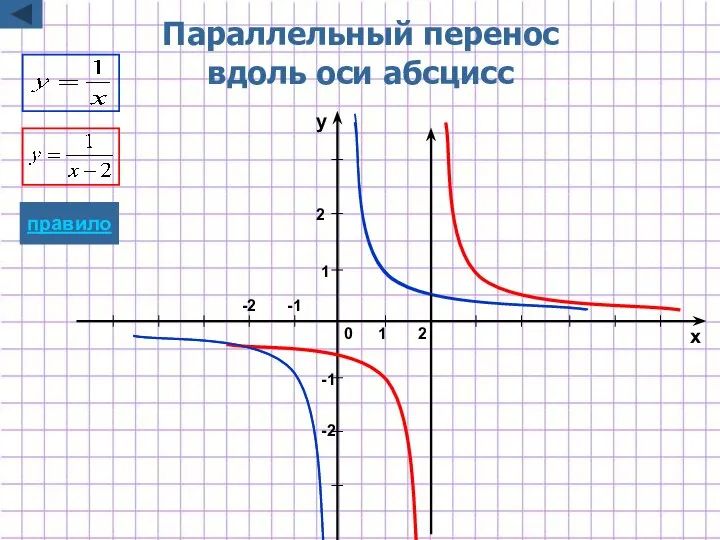
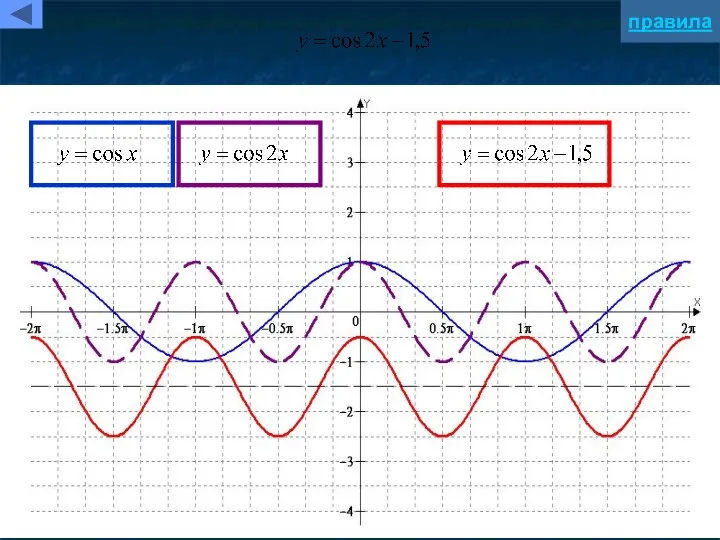
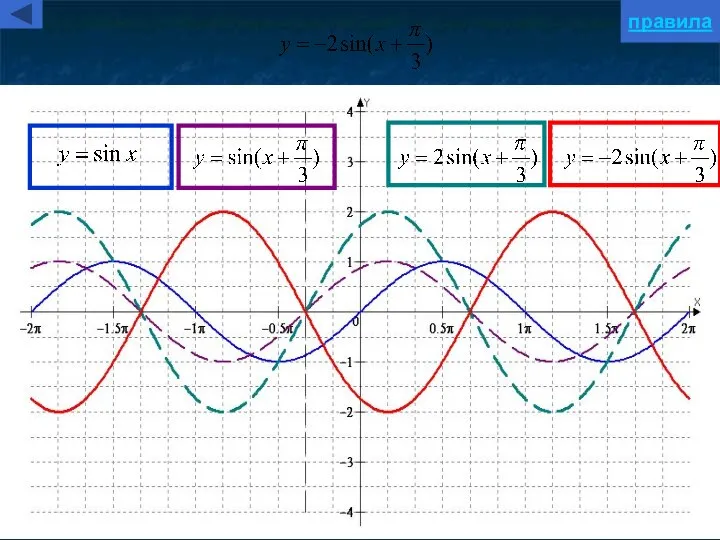
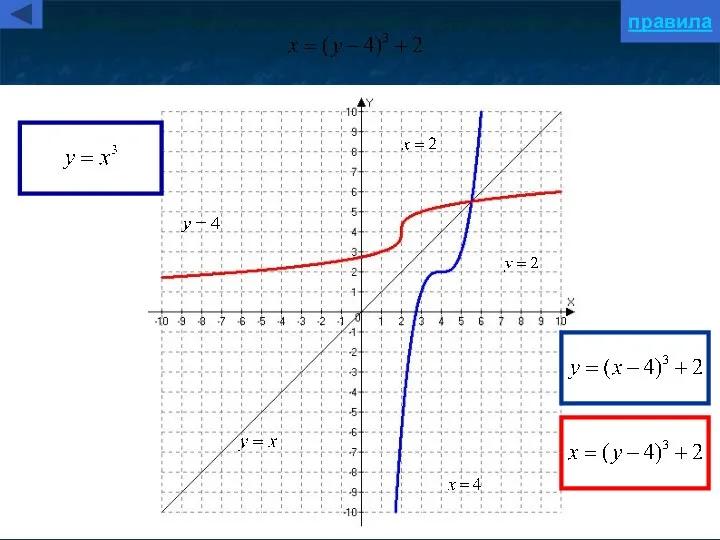
Параллельный перенос
вдоль оси абсцисс
y=f(x+a)
Для построения графика функции y=f(x+a)
надо график функции y=f(x) параллельно
перенести на |a| единиц вдоль оси Ox
в положительном направлении, если a<0
в отрицательном направлении, если a>0
графическая иллюстрация

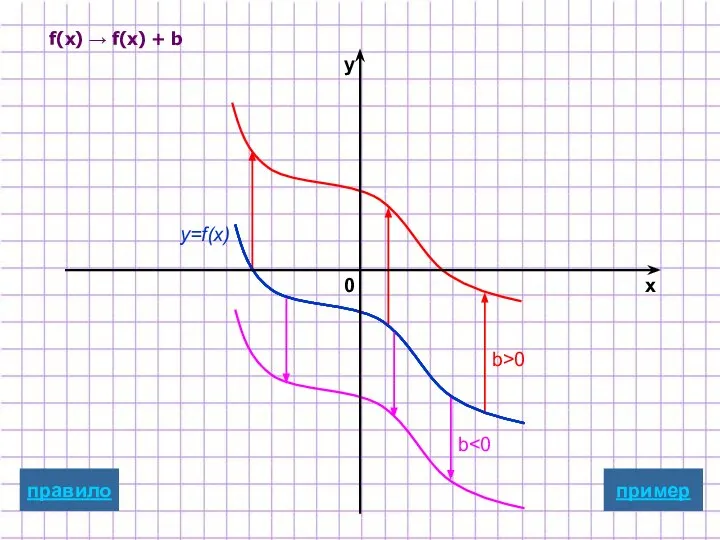
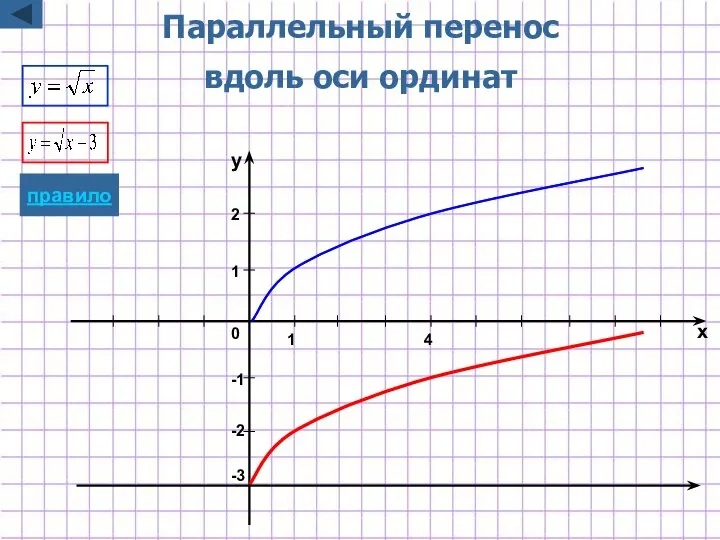
Параллельный перенос
вдоль оси ординат
y=f(x)+b
Для построения графика функции y=f(x)+b
надо график функции y=f(x) параллельно
перенести на |b| единиц вдоль оси Oy
в положительном направлении, если b>0
в отрицательном направлении, если b<0
графическая иллюстрация

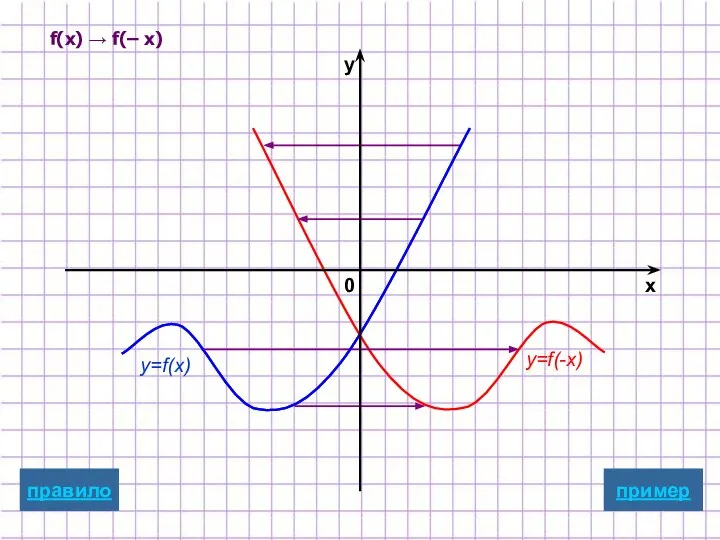
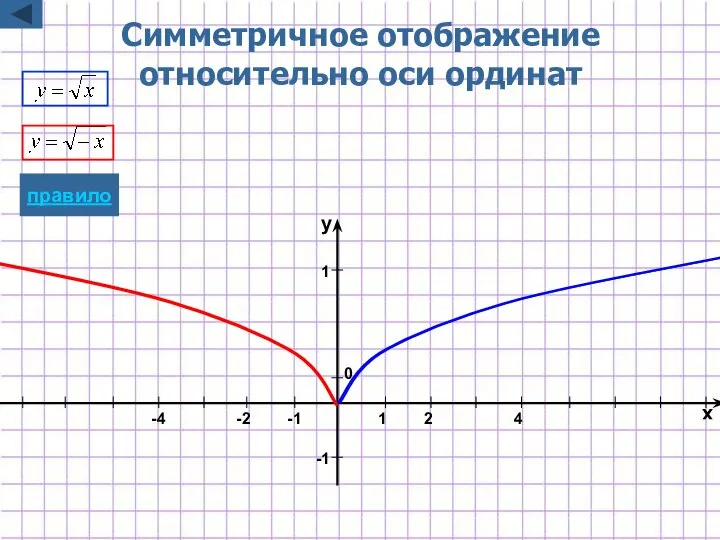
Симметричное отображение
относительно оси ординат
y=f(-x)
Для построения графика функции y=f(-x)
надо график функции y=f(x) симметрично
отобразить относительно оси Oy
Замечание: при этом точки пересечения с осью у остаются неизменными.
графическая иллюстрация

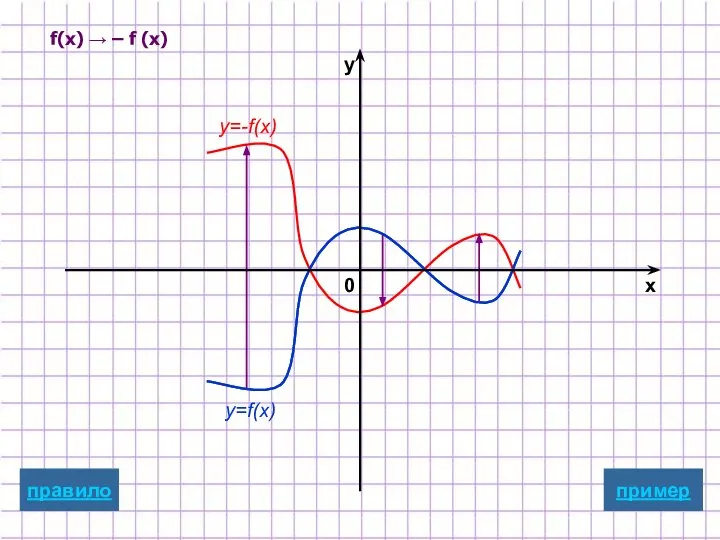
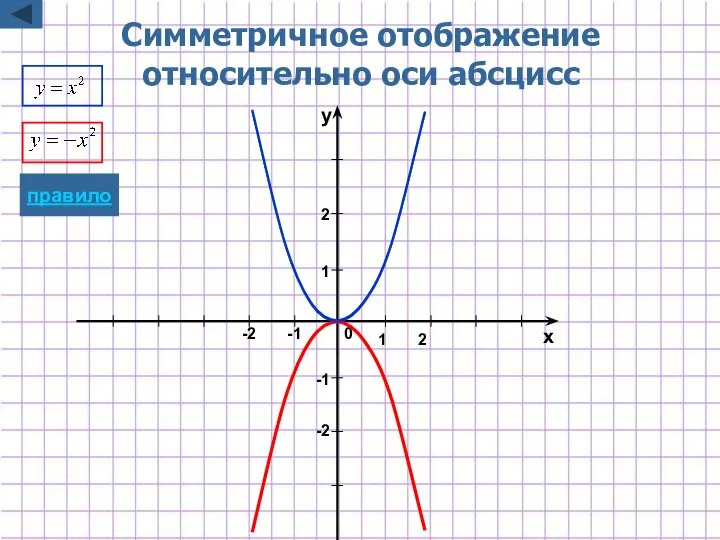
Симметричное отображение
относительно оси абсцисс
y=-f(x)
Для построения графика функции y=-f(x)
надо график функции y=f(x) симметрично
отобразить относительно оси Ox
Замечание: при этом точки пересечения с осью х остаются неизменными.
графическая иллюстрация

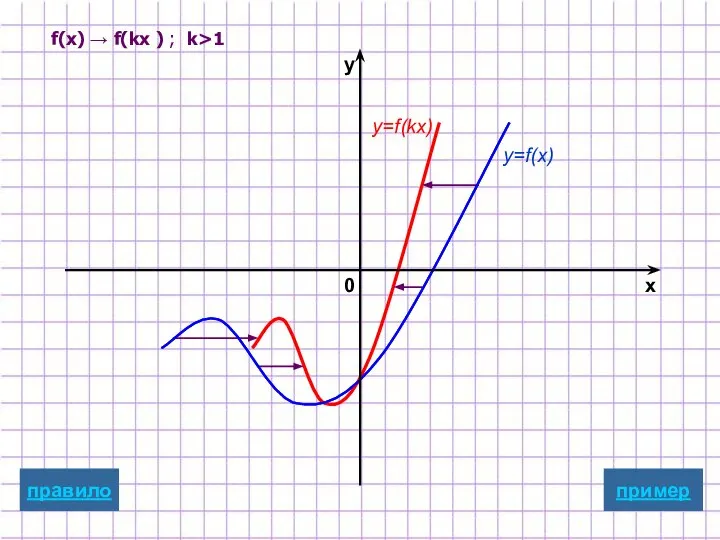
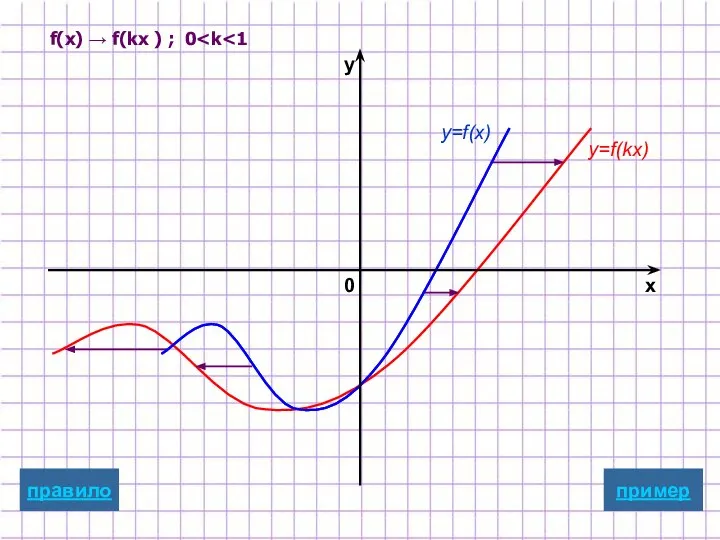
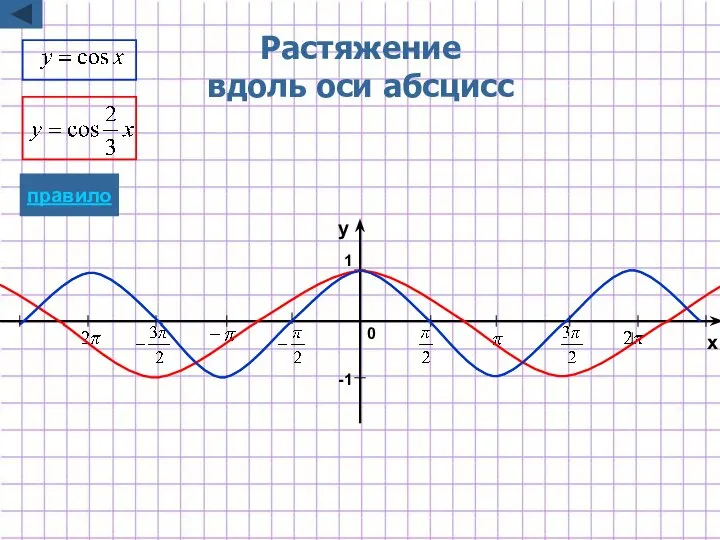
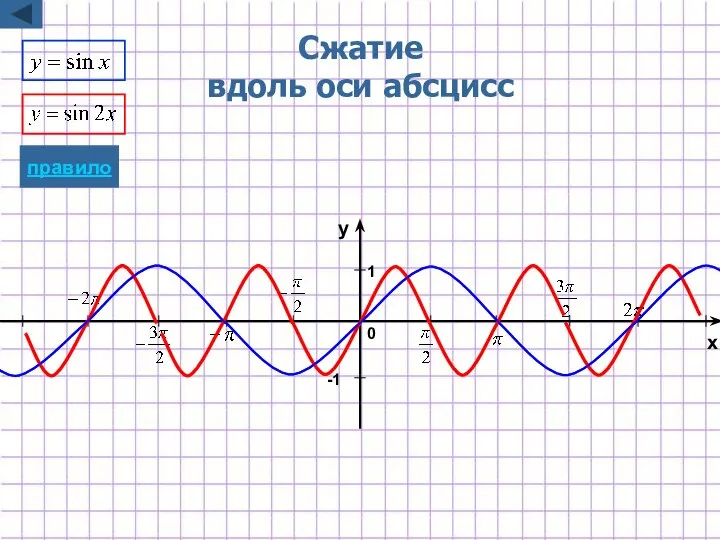
Растяжение/сжатие
вдоль оси абсцисс
y=f(kx)
Для построения графика функции y=f(kx)
надо график функции y=f(x) подвергнуть
масштабированию вдоль оси Ox
растяжению в 1/k раз , если 0
сжатию в k раз, если k>1
Замечание: при этом точки пересечения с осью у остаются неизменными.
графическая иллюстрация 1
графическая иллюстрация 2

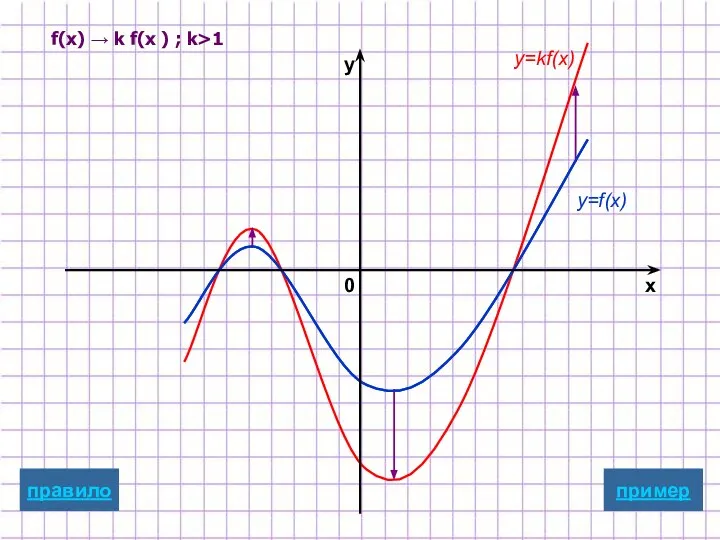
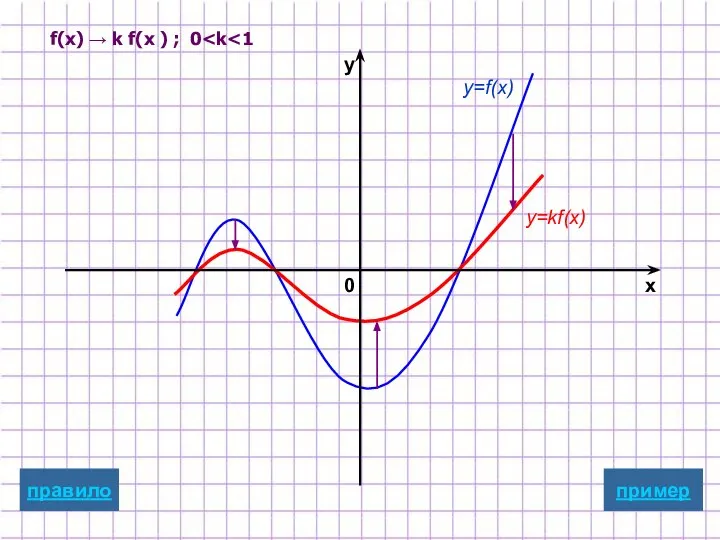
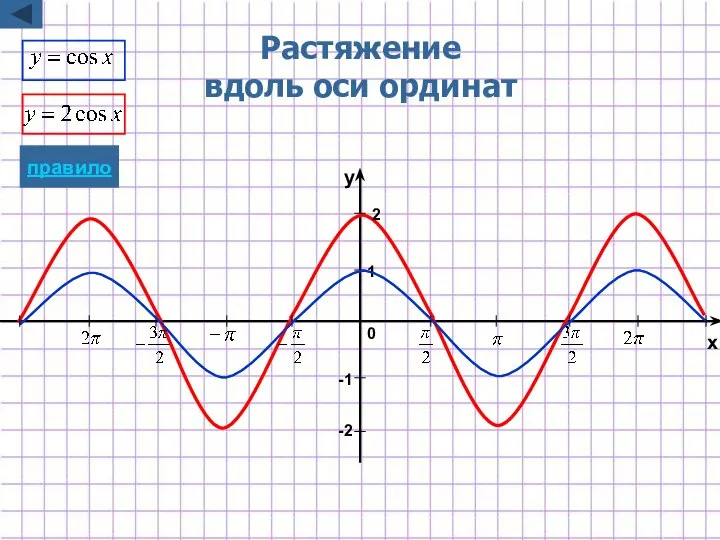
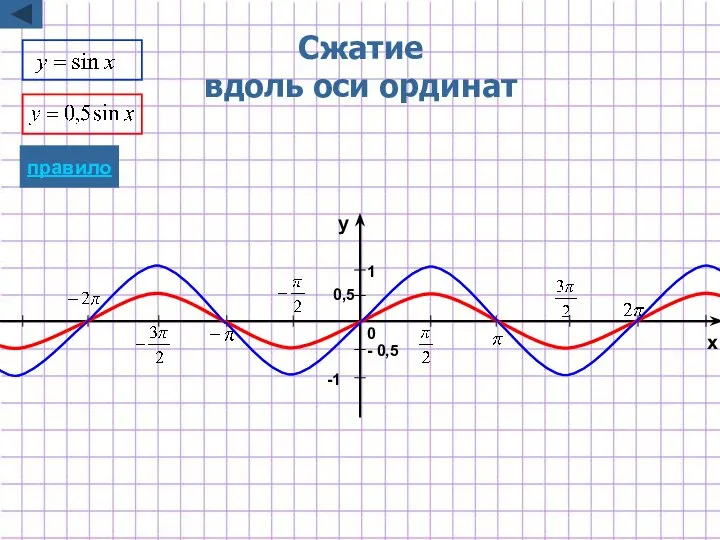
Растяжение/сжатие
вдоль оси ординат
y=kf(x)
Для построения графика функции y=kf(x)
надо график функции y=f(x) подвергнуть
масштабированию вдоль оси Oy
растяжению в k раз , если k>1
сжатию в 1/k раз, если 0
Замечание: при этом точки пересечения с осью х остаются неизменными.
графическая иллюстрация 2
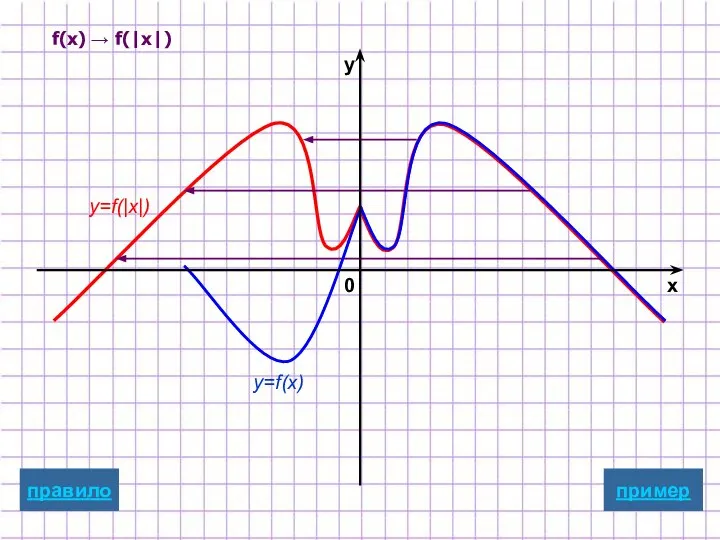
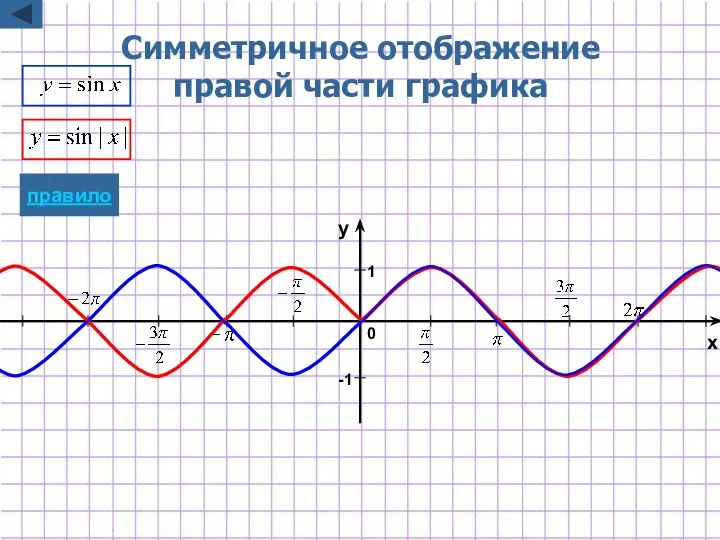
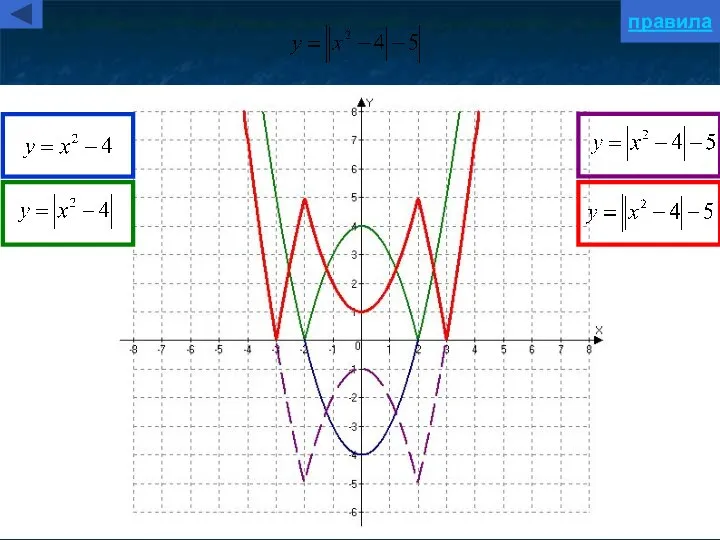
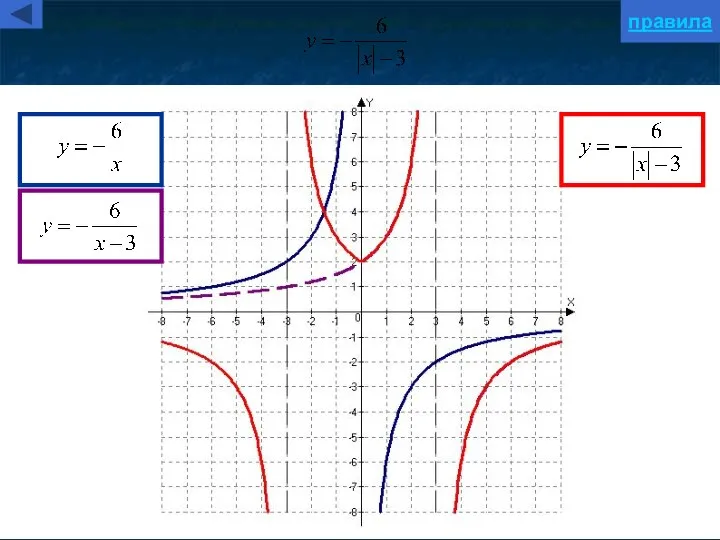
графическая иллюстрация 1

Построение графика y=f(|x|)
y=f(|x|)
Для построения графика функции y=f(|x|) надо:
часть графика функции y=f(x), лежащую правее оси Oy, оставить без изменения;
эту же часть графика функции y=f(x), лежащую правее оси Oy, симметрично отобразить относительно оси Оy
графическая иллюстрация

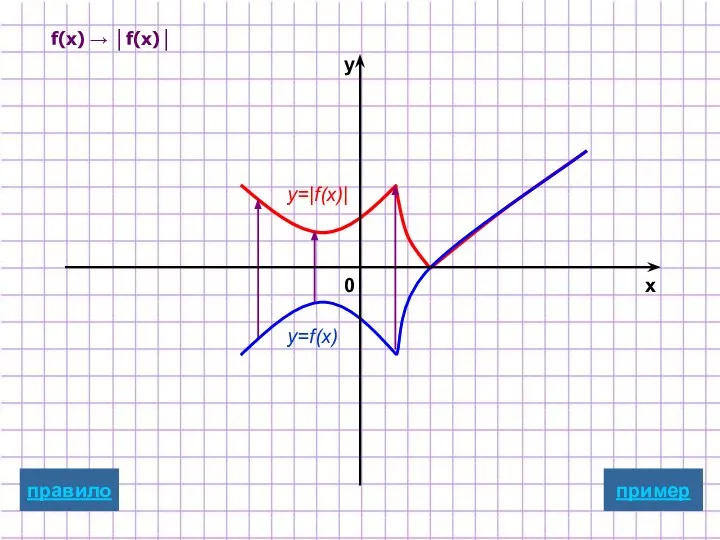
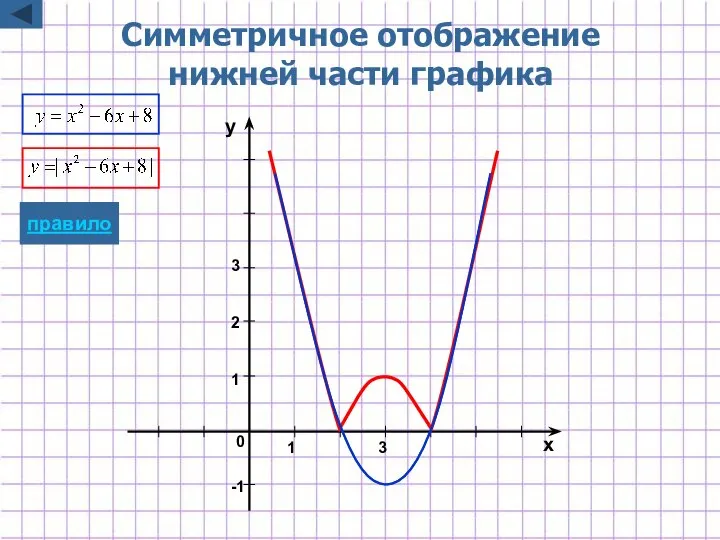
Построение графика y=|f(x)|
y=|f(x)|
Для построения графика функции y=|f(x)| надо:
часть графика функции y=f(x), лежащую выше оси Oх, оставить без изменения;
часть графика функции y=f(x), лежащую ниже оси Oх, симметрично отобразить относительно оси Ох
графическая иллюстрация

Графические иллюстрации
Построение графика функции y=f(x+a)
Построение графика функции y=f(x)+b
Построение графика функции y=f(-x)
Построение графика функции y=-f(x)
Построение графика функции y=f(kx), 0
Построение графика функции y=f(kx), k>1
Построение графика функции y=kf(x), 0
Построение графика функции y=kf(x), k>1
Построение графика функции y=f(|x|)
Построение графика функции y=|f(x)|
оглавление
примеры
правила

f(x) → f(x) + b
b>0
b<0
y=f(x)
пример
x
y
0
правило

f(x) → f(x + а)
a<0
a>0
y=f(x)
пример
x
y
0
правило

f(x) → – f (x)
y=f(x)
y=-f(x)
пример
x
y
0
правило

f(x) → f(– x)
y=f(x)
y=f(-x)
пример
x
y
0
правило

y=f(x)
y=kf(x)
пример
x
y
0
f(x) → k f(x ) ; k>1
правило

y=f(x)
y=kf(x)
пример
x
y
0
f(x) → k f(x ) ; 0
правило

f(x) → f(kx ) ; k>1
y=f(x)
y=f(kx)
пример
x
y
0
правило

f(x) → f(kx ) ; 0
y=f(x)
y=f(kx)
пример
x
y
0
правило

f(x) → │f(x)│
y=f(x)
y=|f(x)|
пример
x
y
0
правило

y=f(x)
y=f(|x|)
пример
x
y
0
f(x) → f(|x|)
правило

Примеры построения графиков сложных функций
Построение графика функции y=f(x+a)
Построение графика функции y=f(x)+b
Построение графика функции y=f(-x)
Построение графика функции y=-f(x)
Построение графика функции y=f(kx), 0
Построение графика функции y=f(kx), k>1
Построение графика функции y=kf(x), 0
Построение графика функции y=kf(x), k>1
Построение графика функции y=f(|x|)
Построение графика функции y=|f(x)|
оглавление

-2
-1
1
2
x
y
1
2
0
Параллельный перенос
вдоль оси абсцисс
-1
-2
правило

-2
-1
1
2
x
y
1
4
0
-3
Параллельный перенос
вдоль оси ординат
правило

-2
-1
1
2
x
y
1
2
0
Симметричное отображение
относительно оси абсцисс
-1
-2
правило

-1
1
x
y
1
2
0
Симметричное отображение
относительно оси ординат
-1
-2
4
-4
правило

Растяжение
вдоль оси ординат
-2
-1
1
2
x
y
0
правило

Сжатие
вдоль оси ординат
- 0,5
-1
1
0,5
x
y
0
правило

Растяжение
вдоль оси абсцисс
-1
1
x
y
0
правило

Сжатие
вдоль оси абсцисс
-1
1
x
y
0
правило

-1
1
2
x
y
1
0
3
3
Симметричное отображение
нижней части графика
правило

Симметричное отображение
правой части графика
-1
1
x
y
0
правило

Примеры построения графиков сложных функций
оглавление

правила

правила

правила

правила

правила