Неисключенные остатки систематической погрешности. Статистическая обработка однократных наблюдений. Случайные погрешности

Неисключенные остатки систематической погрешности
- некий доверительный интервал
- доверительная вероятность попадания в этот интервал
К неисключенным остаткам в случае электрических измерений можно отнести:
размытость сопротивления модели
инструментальные погрешности
личностные погрешности (погрешности оператора)
погрешности, обусловленные размытостью внутреннего сопротивления средства измерения

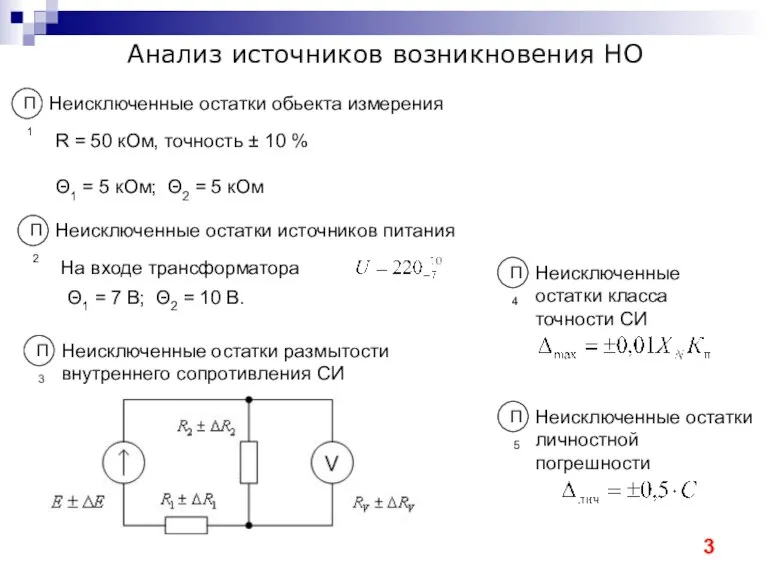
Анализ источников возникновения НО
Неисключенные остатки обьекта измерения
R = 50 кОм, точность ± 10 %
Θ1 = 5 кОм; Θ2 = 5 кОм
Неисключенные остатки источников питания
Θ1 = 7 В; Θ2 = 10 В.
На входе трансформатора
Неисключенные остатки размытости внутреннего сопротивления СИ
Неисключенные остатки класса точности СИ
Неисключенные остатки
личностной погрешности

Результирующая погрешность (композиция) неисключенных остатков определяется выражением:
Запись результата измерений:

Общий алгоритм обработки однократных наблюдений
1. Определение методической погрешности измерений
2. Определение поправки
3. Определение оценочного значения результата измерения
4. Определение неисключенных остатков систематической погрешности
5. Определение границ доверительного интервала
6. Запись результата измерения

Случайные погрешности
Вероятностный подход к описанию погрешностей
Случайными называют составляющие погрешности измерений, изменяющиеся случайным образом при повторных измерениях одной и той же величины.
- случайная погрешность
- среднее квадратическое отклонение
- плотность распределения

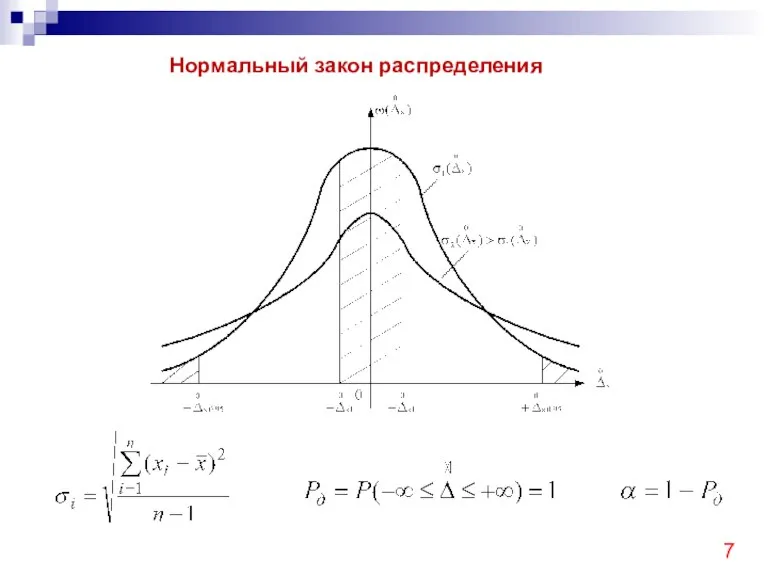
Нормальный закон распределения

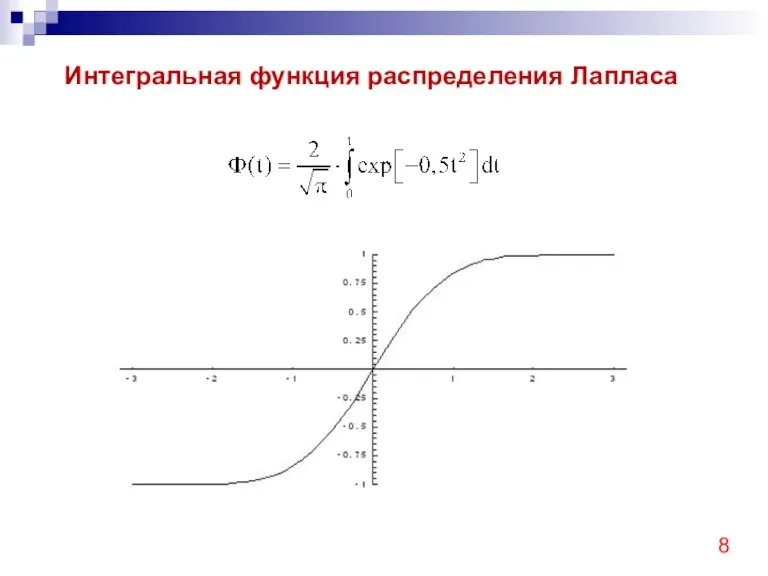
Интегральная функция распределения Лапласа

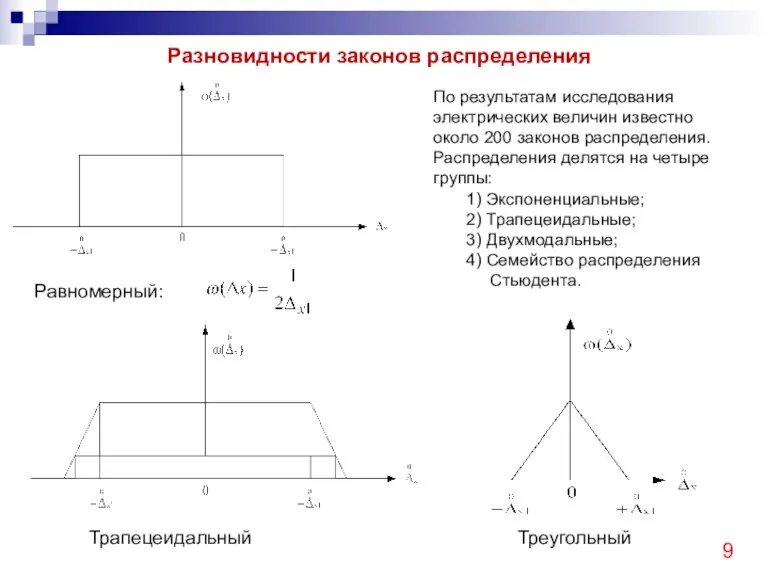
Разновидности законов распределения
По результатам исследования электрических величин известно около 200 законов распределения.
Распределения делятся на четыре группы:
1) Экспоненциальные;
2) Трапецеидальные;
3) Двухмодальные;
4) Семейство распределения
Стьюдента.
Равномерный:
Треугольный
Трапецеидальный

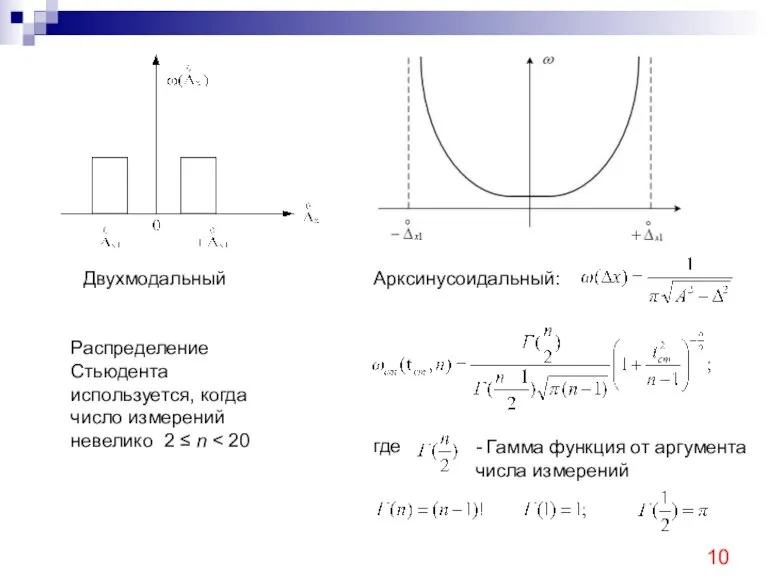
Двухмодальный
Арксинусоидальный:
Распределение Стьюдента используется, когда число измерений невелико 2 ≤ n < 20
где
- Гамма функция от аргумента числа измерений

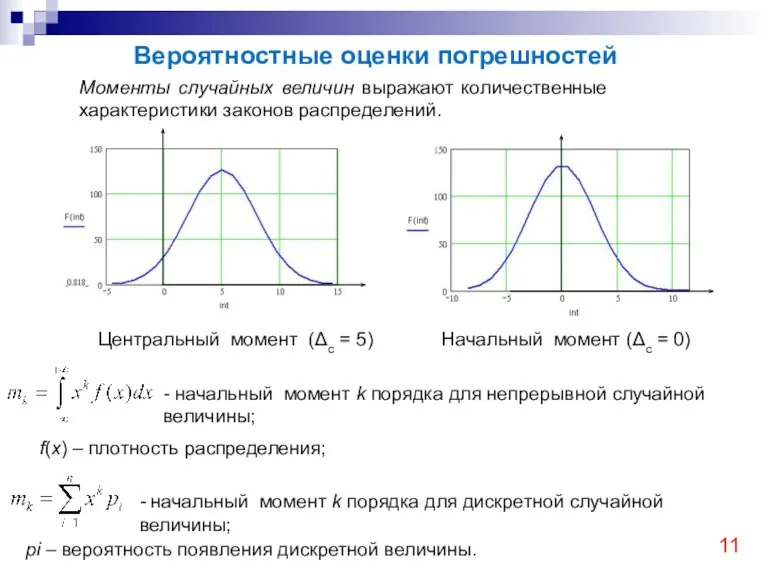
Вероятностные оценки погрешностей
Моменты случайных величин выражают количественные характеристики законов распределений.
Начальный момент (Δс = 0)
Центральный момент (Δс = 5)
- начальный момент k порядка для непрерывной случайной величины;
f(x) – плотность распределения;
- начальный момент k порядка для дискретной случайной величины;
pi – вероятность появления дискретной величины.

1. Момент первого порядка характеризует математическое ожидание – неслучайную величину, относительно которой рассеиваются другие значения при повторных измерениях.
- для непрерывной случайной величины;
- для дискретной случайной величины;
2. Момент второго порядка характеризует дисперсию – степень рассеяния (разброса) отдельных значений относительно матожидания.
- для непрерывной случайной величины;
- для дискретной случайной величины;
- среднее квадратической отклонение (СКО);

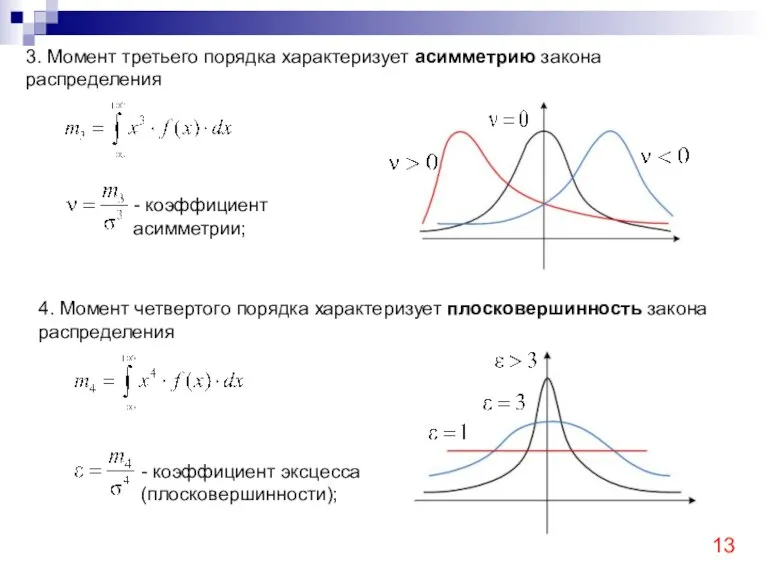
3. Момент третьего порядка характеризует асимметрию закона распределения
- коэффициент асимметрии;
4. Момент четвертого порядка характеризует плосковершинность закона распределения
- коэффициент эксцесса (плосковершинности);

Практическое применение связи между доверительной вероятностью и функциями Стьюдента и Лапласа
Если число измерений больше или равно 20
Если число измерений меньше 20
СКО среднего арифметического