Логарифмы

Анатоль Франс (1844–1924)
французский писатель
«Что учиться можно только весело... Чтобы переварить знания, надо поглощать их с аппетитом».

Условия и правила игры:
1. Каждая команда выбирает капитана.
2. Побеждает та команда, которая первой придет к финишу.
3. В личном первенстве победителем становится учащийся, набравший наибольшее количество очков (километров).
4. Участники игры имеют право обращаться в «консультационный пункт» – стол, на котором разложены учебная и научная литература, справочники, решения типовых заданий.
5. Эстафета состоит из четырех этапов, в ходе которых вы покажете:
а) знания свойств, определений (1 задание)
б) умения устно вычислять (2 задание)
в) умения читать график (3 задание)
г) умения решать уравнения и неравенства (4 задание)

Задание1.1
«Математические термины»

кроссворд

Задание1.2 «Выбери вопрос»

Задание 1.3
«Графический диктант»
1. Логарифмическая функция у = logax определена при любом х
2. Функция у = logax определена при а > 0, а =/= 1, х > 0.
3. Областью определения логарифмической функции является множество действительных чисел.
4. Областью значений логарифмической функции является множество действительных чисел.
5. Логарифмическая функция – четная.
6. Логарифмическая функция – нечетная.
7. Функция у = logax – возрастающая при а >1.

8. Функция у = logax при положительном, но меньшем единицы основании, – возрастающая.
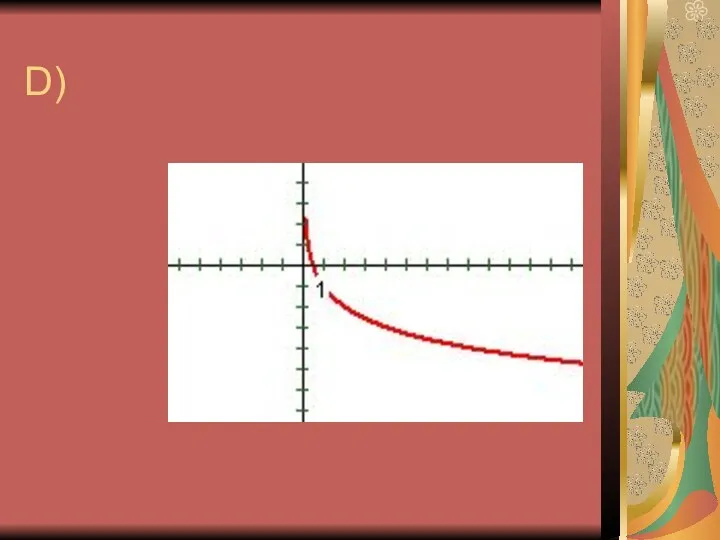
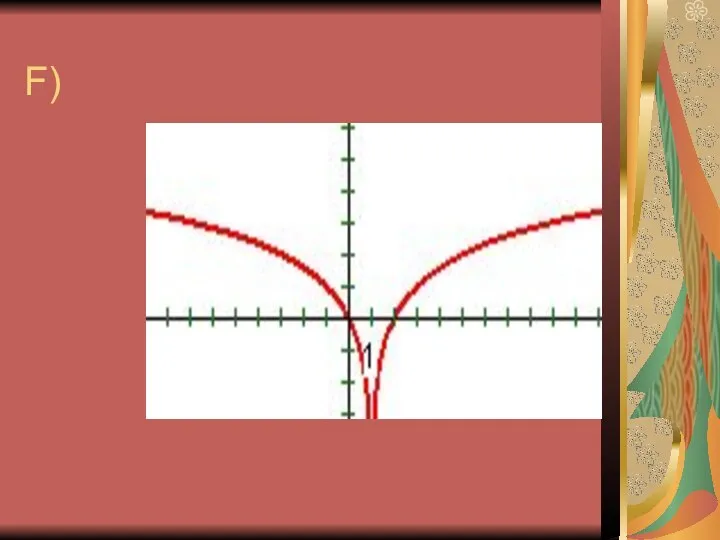
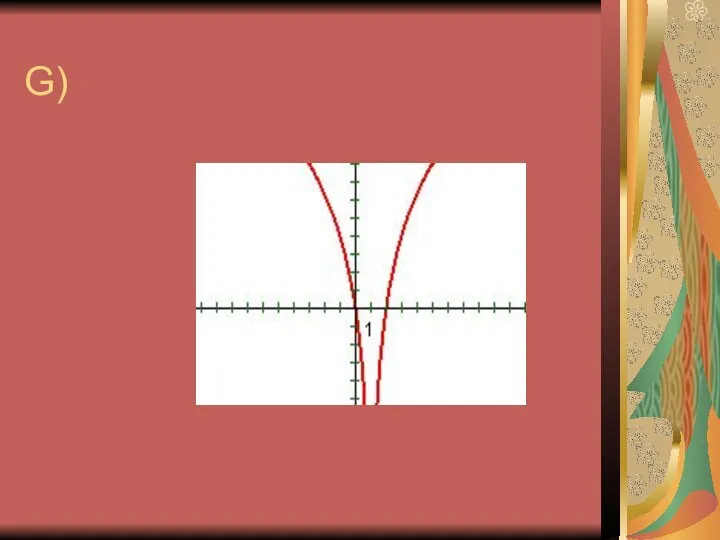
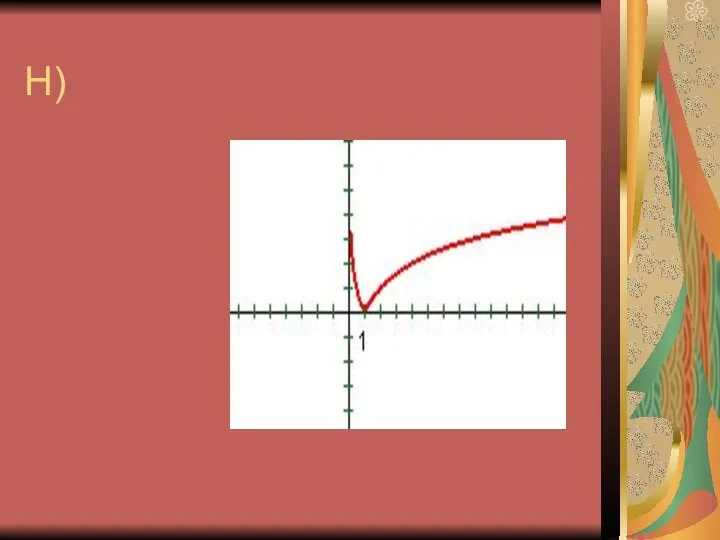
9. Логарифмическая функция имеет экстремум в точке (1; 0).
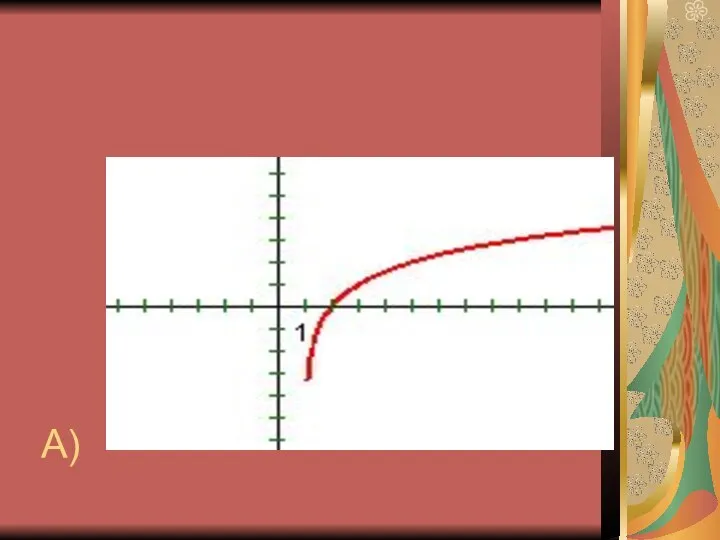
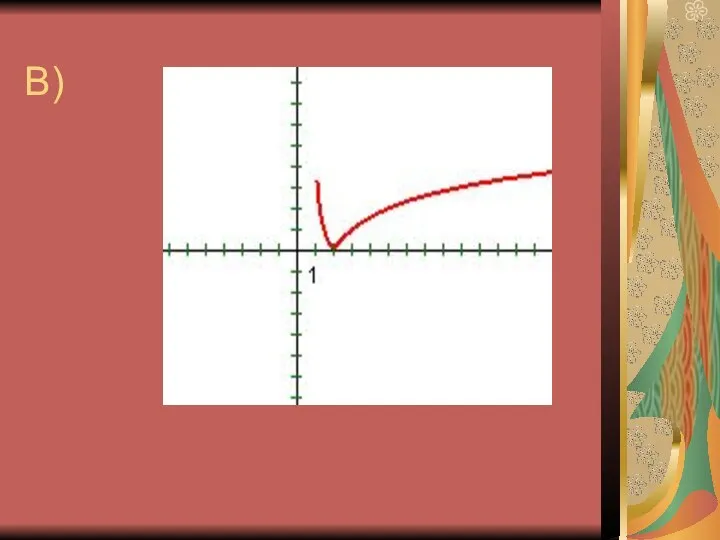
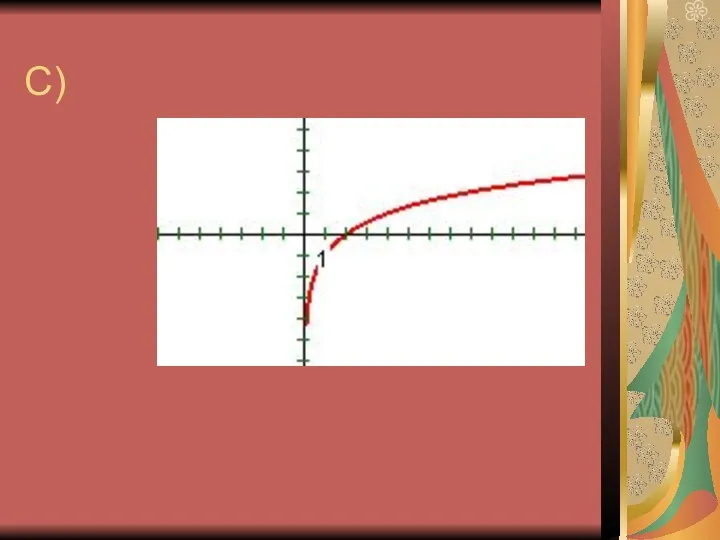
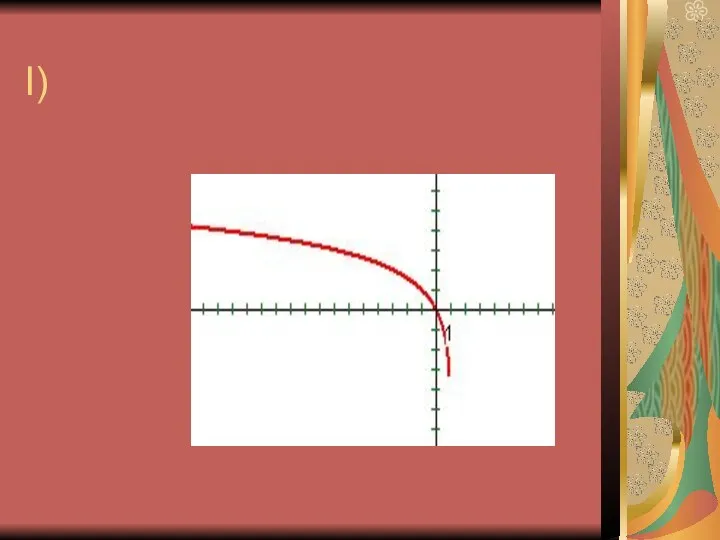
10. График функции у = logax пересекается с осью ОХ.
11. График логарифмической функции находится в верхней полуплоскости.
12. График логарифмической функции симметричен относительно ОХ.
13. График логарифмической функции пересекает ОХ
в точке (1; 0).
14. График логарифмической функции находится в 1 и 4 четвертях.
15. Существует логарифм отрицательного числа.
16. Существует логарифм дробного положительного числа.
17. График логарифмической функции проходит через точку (0; 0).

Задание 2 «Перестрелка»

Задание3 «Графики»

А)

B)

C)

D)

F)

G)

H)

I)