Вписанная и описанная окружности

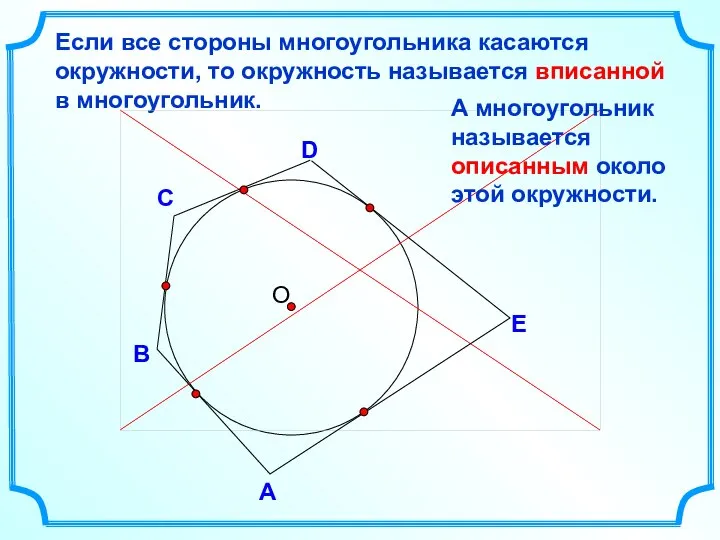
D
В
С
Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник.
А
E
А многоугольник называется описанным около этой окружности.

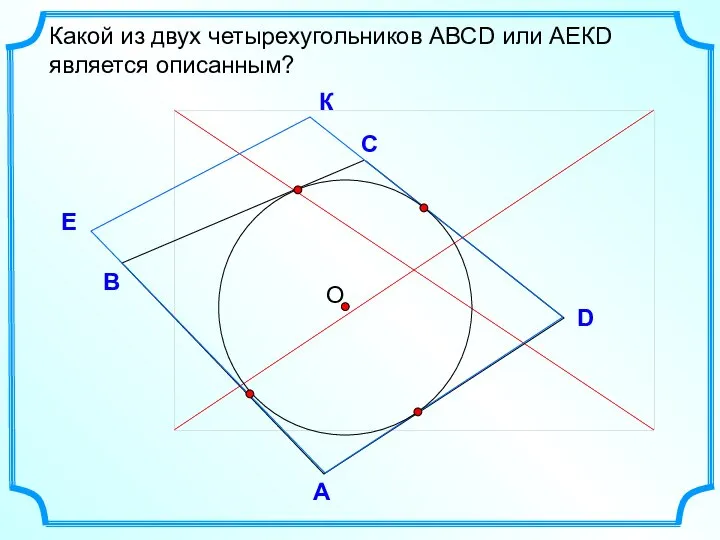
D
В
С
Какой из двух четырехугольников АВСD или АЕКD является описанным?
А
E
К

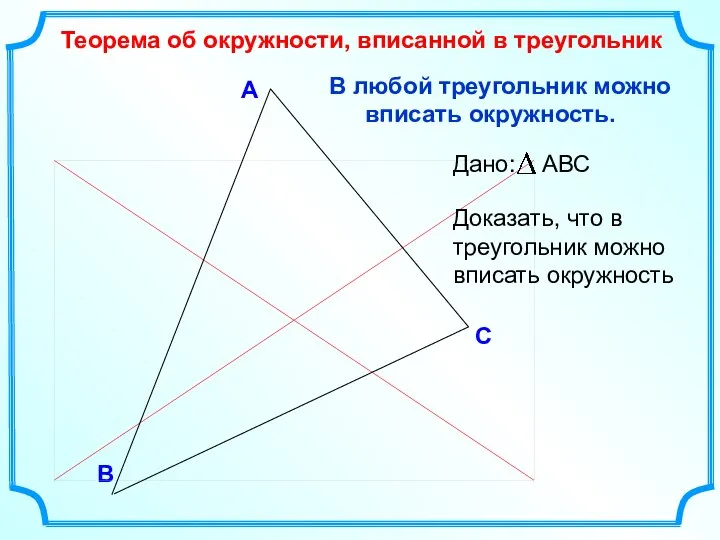
В
С
А
В любой треугольник можно вписать окружность.
Теорема об окружности, вписанной в треугольник
Доказать, что в треугольник можно вписать окружность

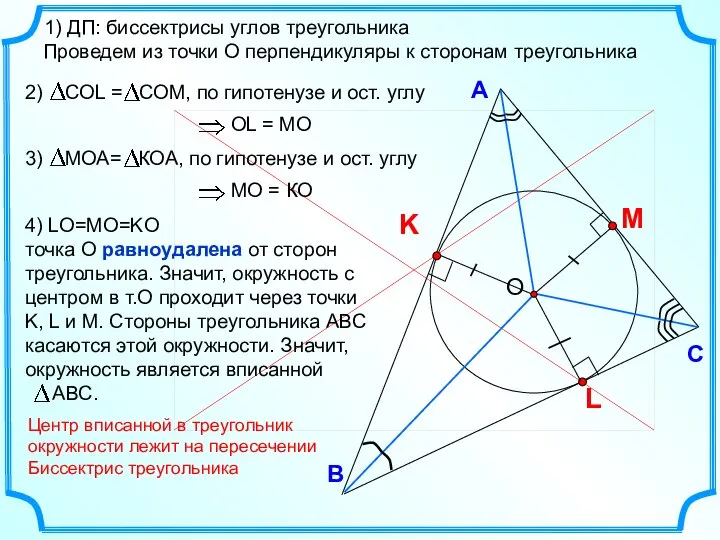
В
С
А
1) ДП: биссектрисы углов треугольника
Проведем из точки О перпендикуляры к сторонам треугольника
Центр вписанной в треугольник
окружности лежит на пересечении
Биссектрис треугольника

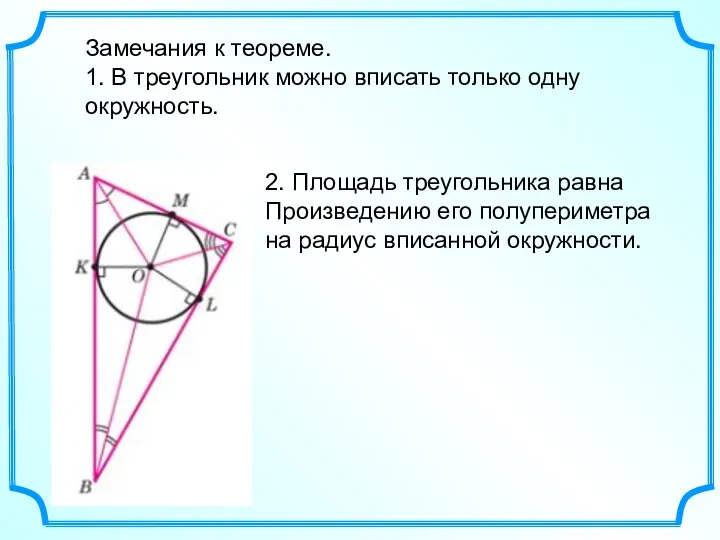
Замечания к теореме.
1. В треугольник можно вписать только одну окружность.
2. Площадь треугольника равна
Произведению его полупериметра
на радиус вписанной окружности.

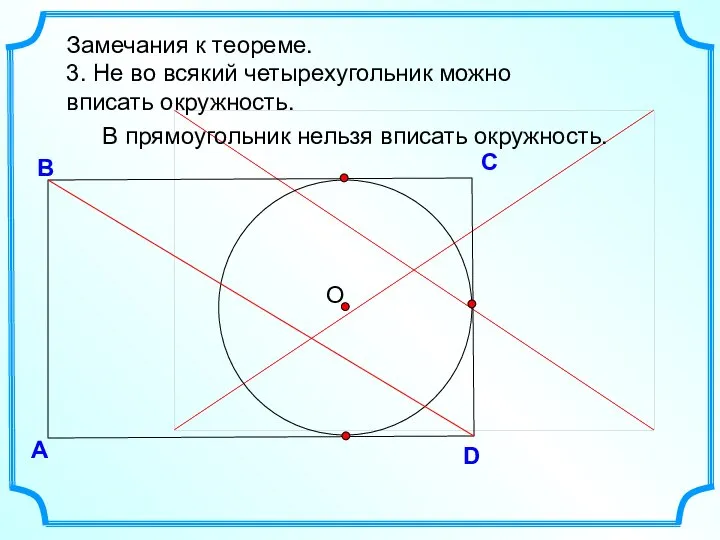
D
В
С
А
Замечания к теореме.
3. Не во всякий четырехугольник можно вписать окружность.
В прямоугольник нельзя вписать окружность.

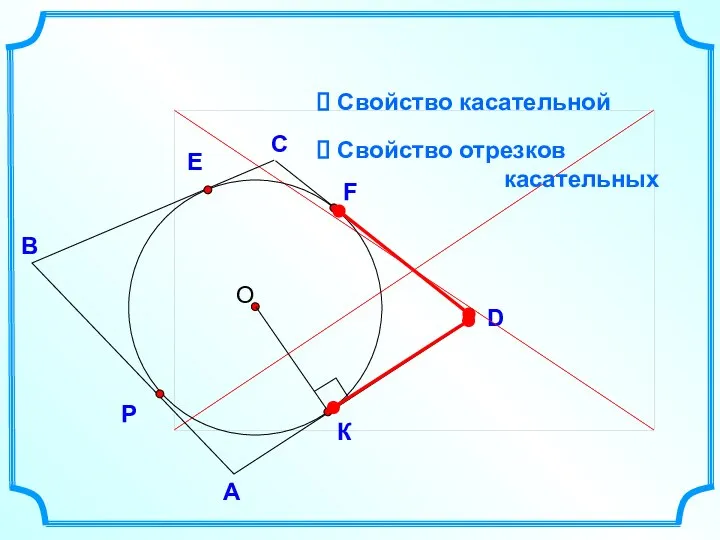
Ели в четырехугольник можно
вписать окружность,
то он должен обладать
следующими свойствами,
для доказательства которых нужно вспомнить

D
В
С
А
E
Свойство касательной
Свойство отрезков
касательных
F
P

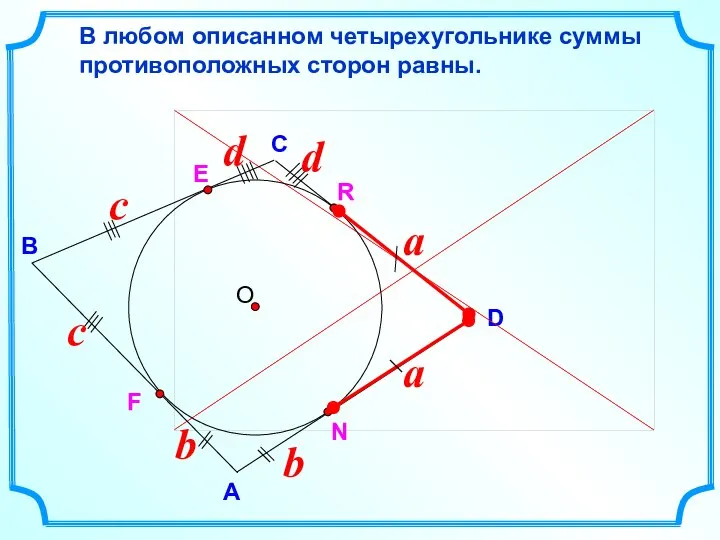
D
В
С
В любом описанном четырехугольнике суммы противоположных сторон равны.
А
E
R
N
F

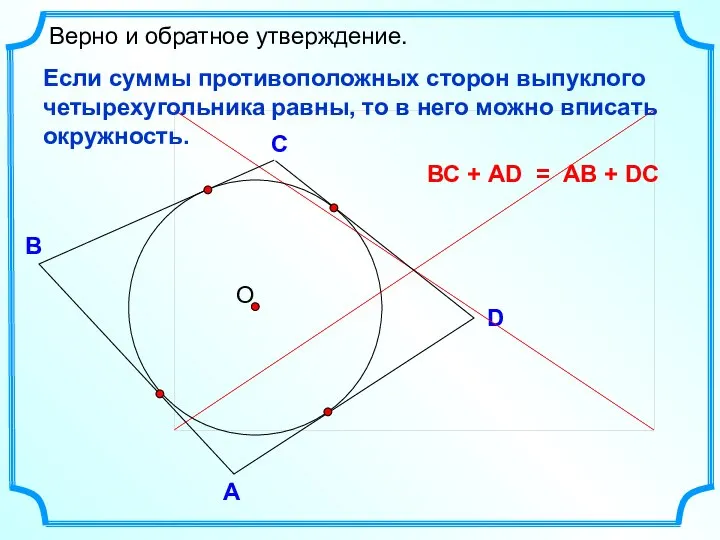
D
В
С
Верно и обратное утверждение.
А
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
ВС + АD = АВ + DC

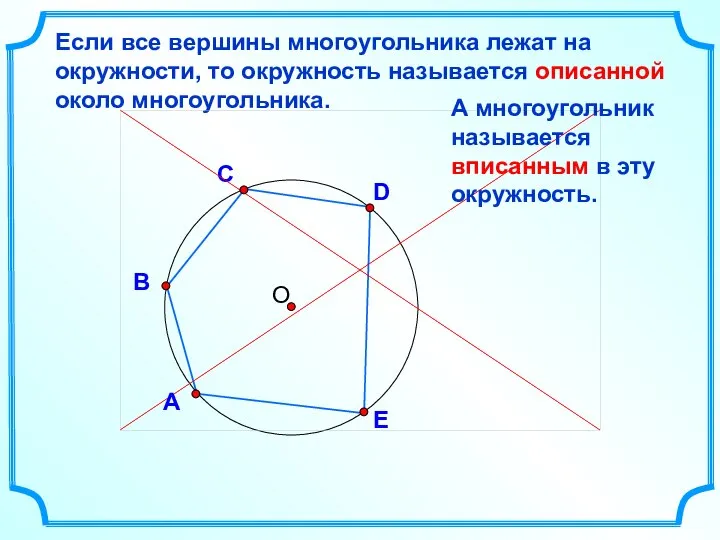
D
В
С
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника.
А
E
А многоугольник называется вписанным в эту окружность.

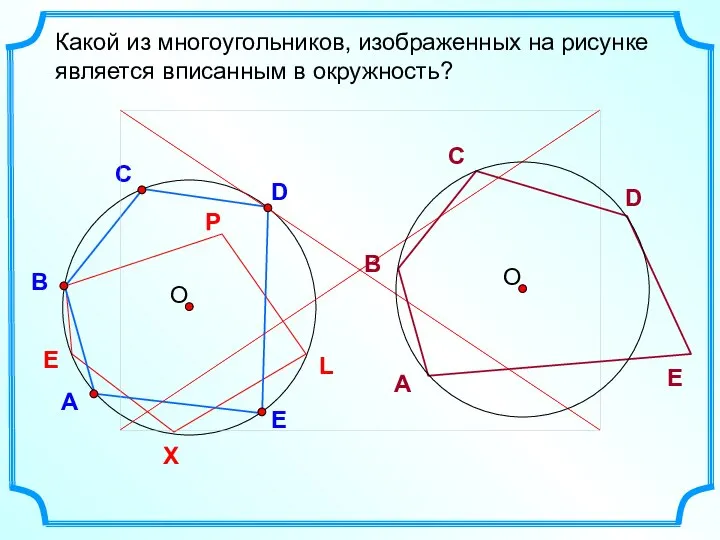
D
В
С
Какой из многоугольников, изображенных на рисунке является вписанным в окружность?
А
E
L
P
X
E

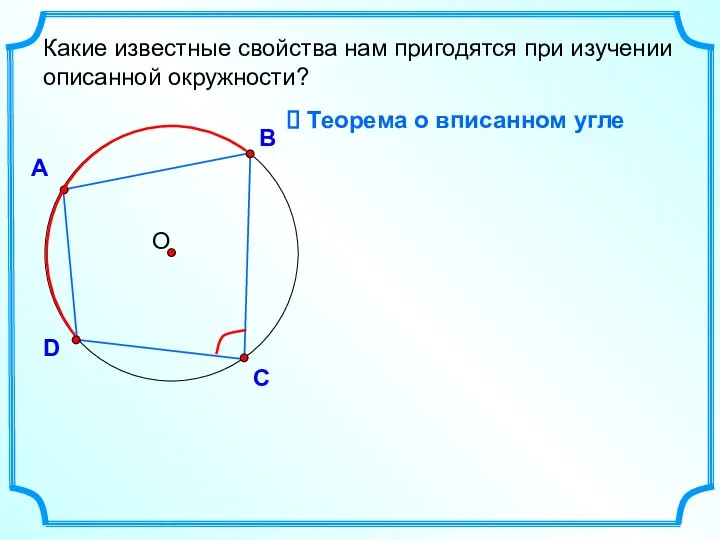
А
В
D
С
Какие известные свойства нам пригодятся при изучении описанной окружности?
Теорема о вписанном угле

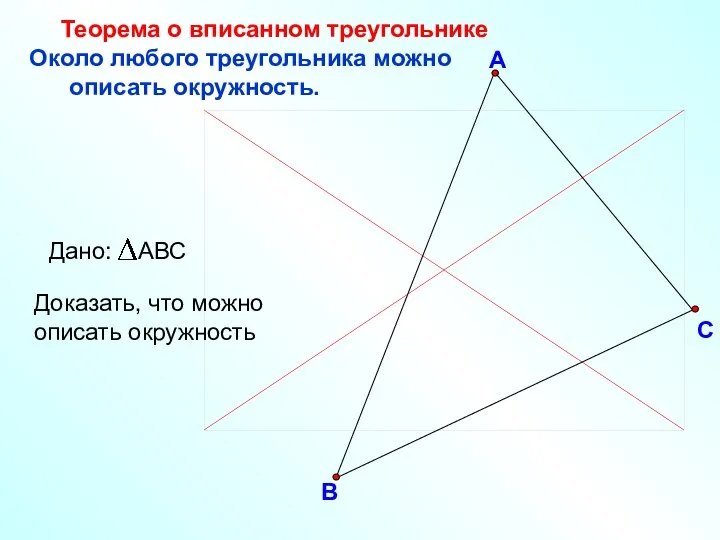
В
С
А
Около любого треугольника можно
описать окружность.
Теорема о вписанном треугольнике
Доказать, что можно описать окружность

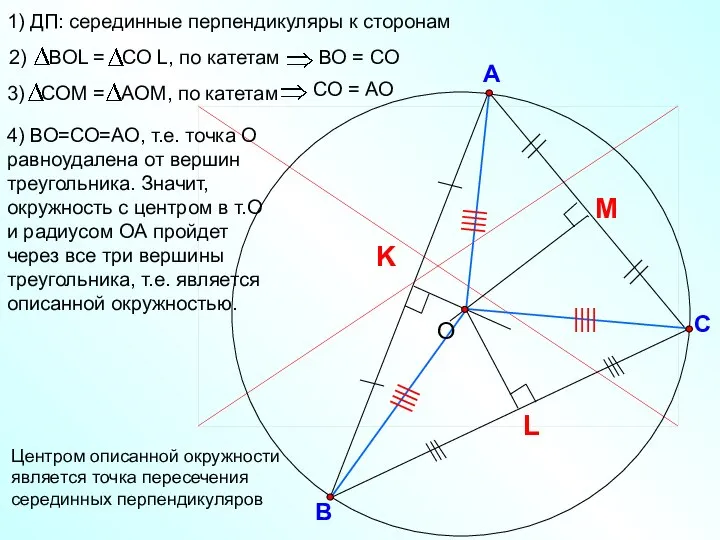
В
С
А
1) ДП: серединные перпендикуляры к сторонам
4) ВО=СО=АО, т.е. точка О равноудалена от вершин треугольника. Значит, окружность с центром в т.О и радиусом ОА пройдет через все три вершины треугольника, т.е. является описанной окружностью.
Центром описанной окружности
является точка пересечения
серединных перпендикуляров

Около треугольника можно описать окружность
и при том только одну.

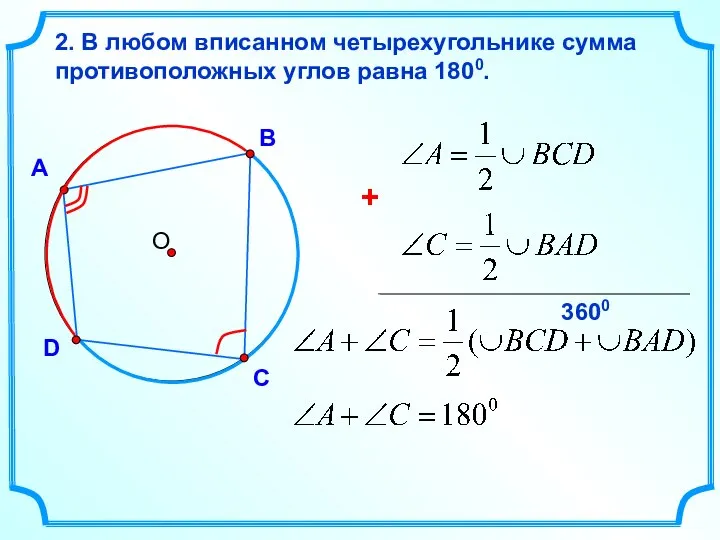
А
В
D
2. В любом вписанном четырехугольнике сумма противоположных углов равна 1800.
С
3600

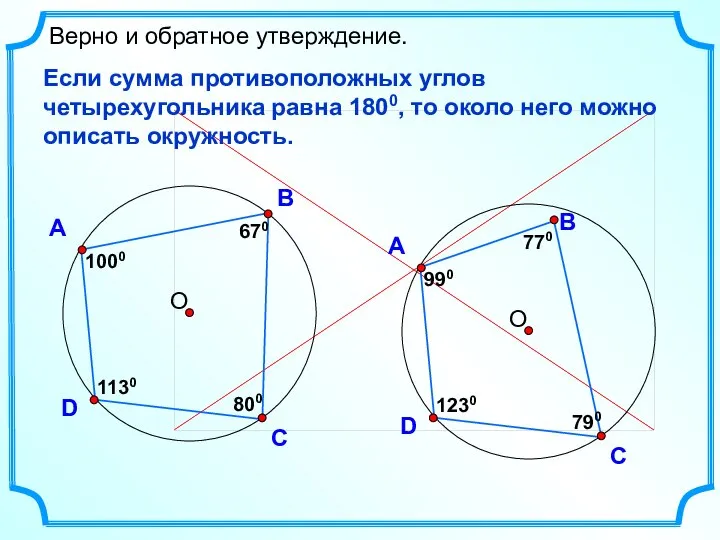
D
Верно и обратное утверждение.
Если сумма противоположных углов четырехугольника равна 1800, то около него можно описать окружность.
А
В
С
800
1000
1130
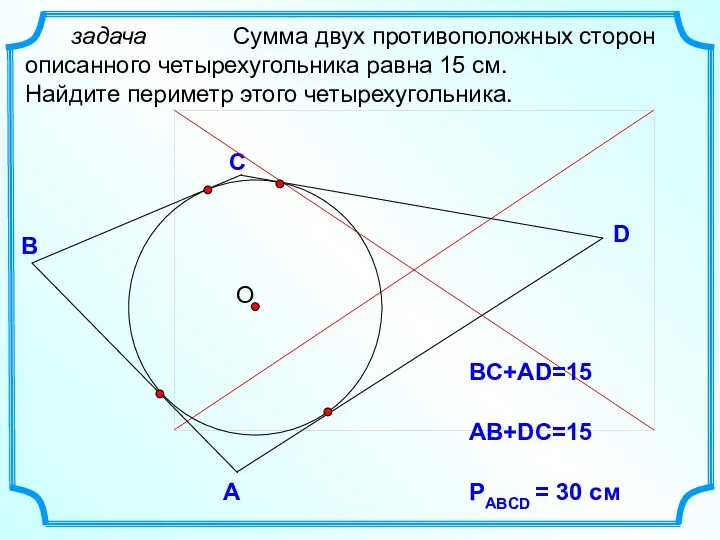
670

D
В
С
задача Сумма двух противоположных сторон описанного четырехугольника равна 15 см.
Найдите периметр этого четырехугольника.
А
ВC+AD=15
AB+DC=15
PABCD = 30 см

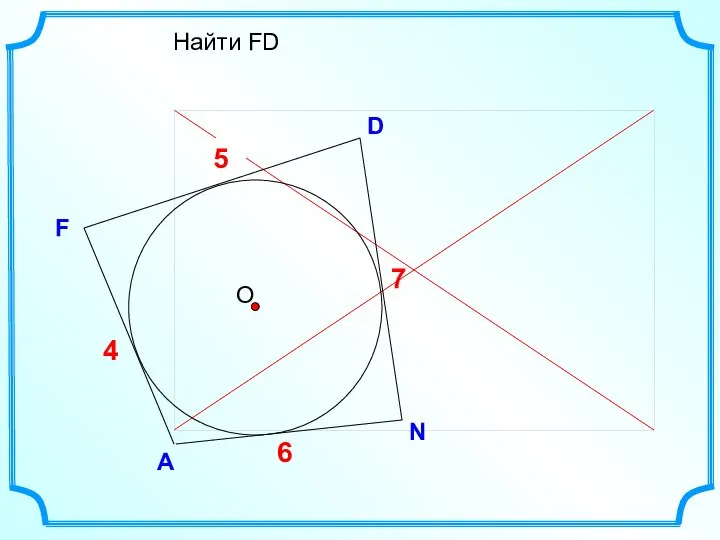
D
F
Найти FD
А
N
?
4
7
6
5

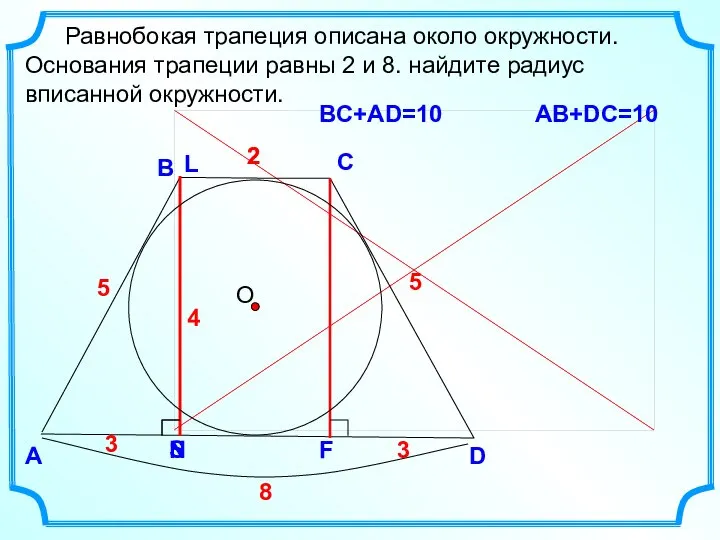
D
В
С
Равнобокая трапеция описана около окружности. Основания трапеции равны 2 и 8. найдите радиус вписанной окружности.
А
ВC+AD=10
AB+DC=10
2
8
2
4