Содержание
- 2. Авторский сайт: vasmirnov.ru
- 5. Геометрическим местом точек (ГМТ) называется фигура, состоящая из всех точек, удовлетворяющих заданному свойству или нескольким заданным
- 6. Серединный перпендикуляр Теорема. Серединный перпендикуляр к отрезку является ГМТ, одинаково удаленных от концов этого отрезка. Серединным
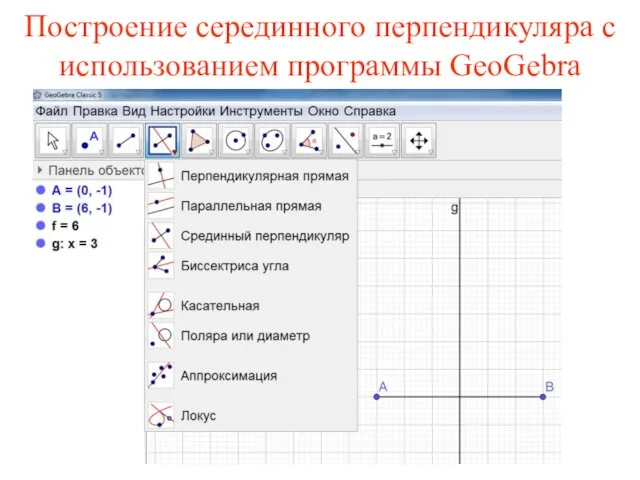
- 7. Построение серединного перпендикуляра с использованием программы GeoGebra
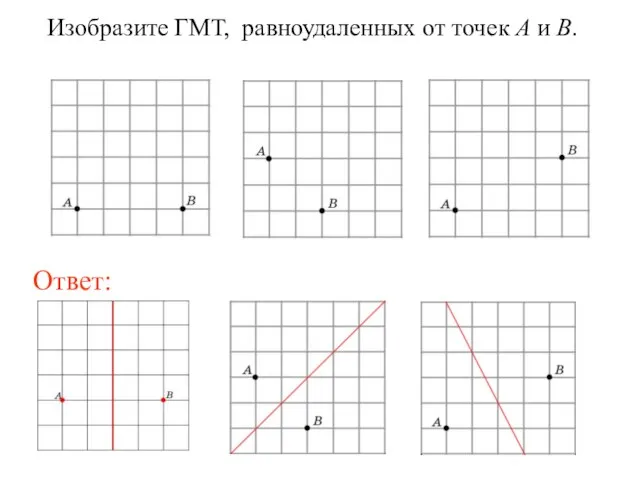
- 8. Изобразите ГМТ, равноудаленных от точек A и B.
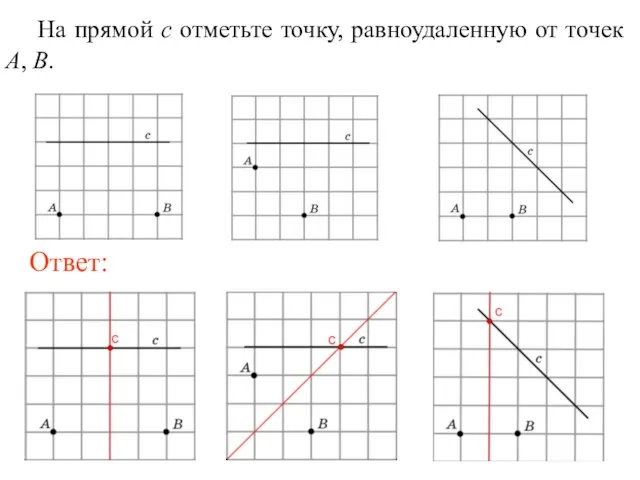
- 9. На прямой c отметьте точку, равноудаленную от точек A, B.
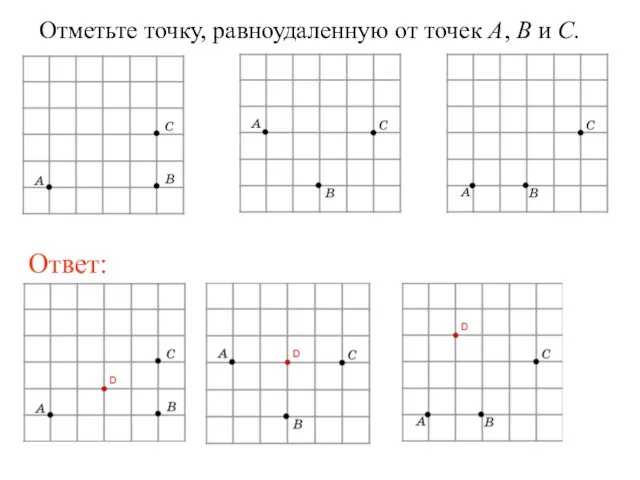
- 10. Отметьте точку, равноудаленную от точек A, B и C.
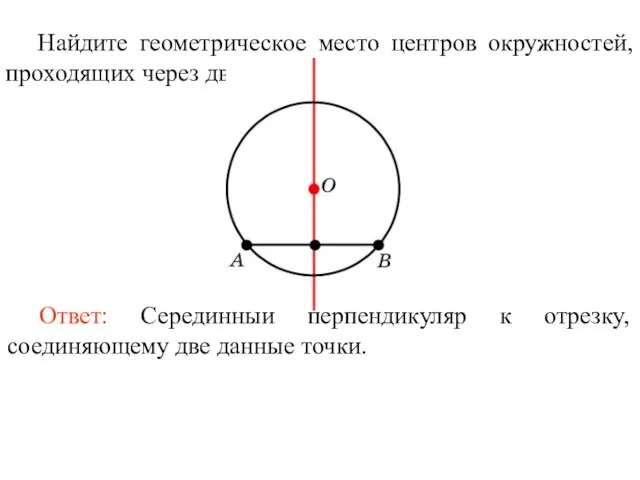
- 11. Найдите геометрическое место центров окружностей, проходящих через две данные точки.
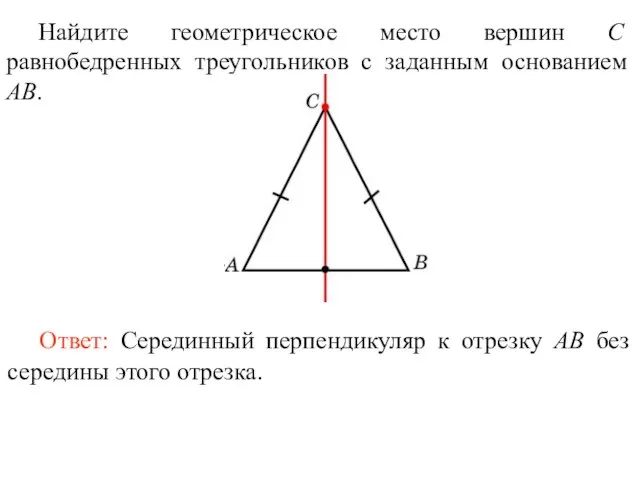
- 12. Найдите геометрическое место вершин С равнобедренных треугольников с заданным основанием AB.
- 13. Для данных точек A и B найдите ГМТ точек, D расстояние от которых до точки A
- 14. Решение. Докажем, что искомым ГМТ является полуплоскость, ограниченная серединным перпендикуляром к отрезку AB, содержащая точку A,
- 15. Пусть А и В точки плоскости, c - прямая. Укажите геометрическое место точек прямой c, расположенных
- 16. (*). Для данных точек A и B изобразите ГМТ, удалённых от A на расстояние, в 2
- 17. Биссектриса угла Если CA = CB, то прямоугольные треугольники АOС и ВOС равны (по гипотенузе и
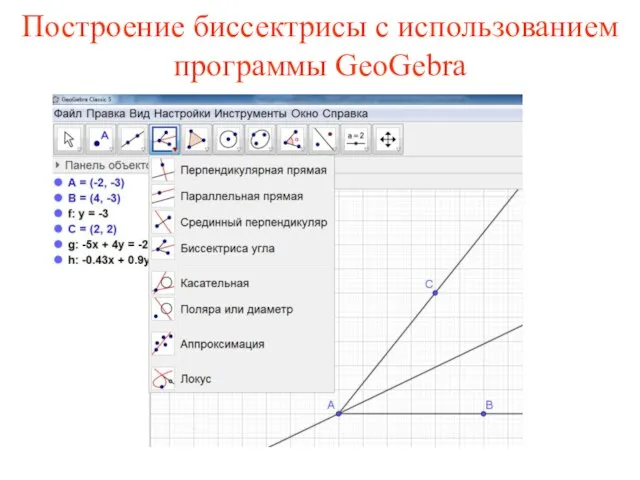
- 18. Построение биссектрисы с использованием программы GeoGebra
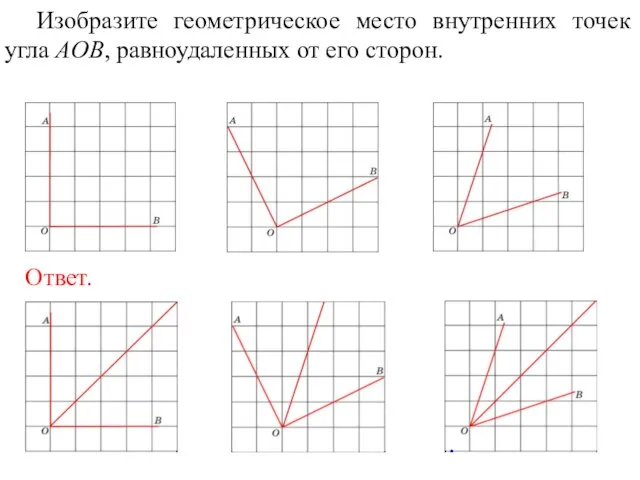
- 19. Изобразите геометрическое место внутренних точек угла AOB, равноудаленных от его сторон.
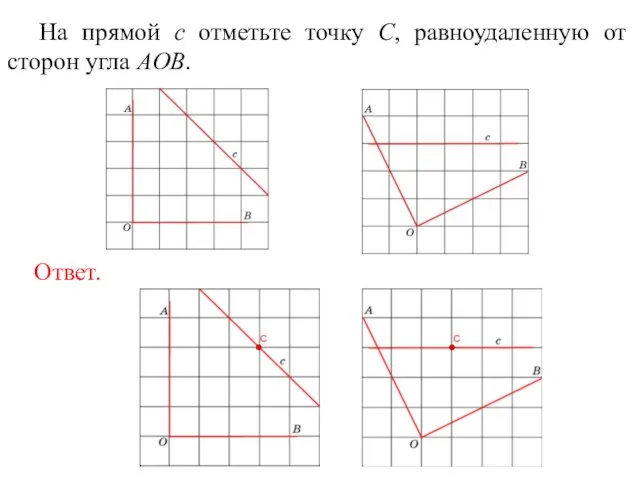
- 20. На прямой c отметьте точку C, равноудаленную от сторон угла AOB.
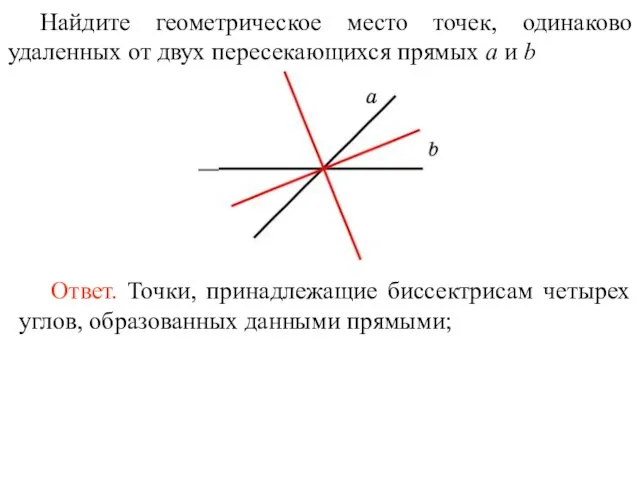
- 21. Найдите геометрическое место точек, одинаково удаленных от двух пересекающихся прямых a и b Ответ. Точки, принадлежащие
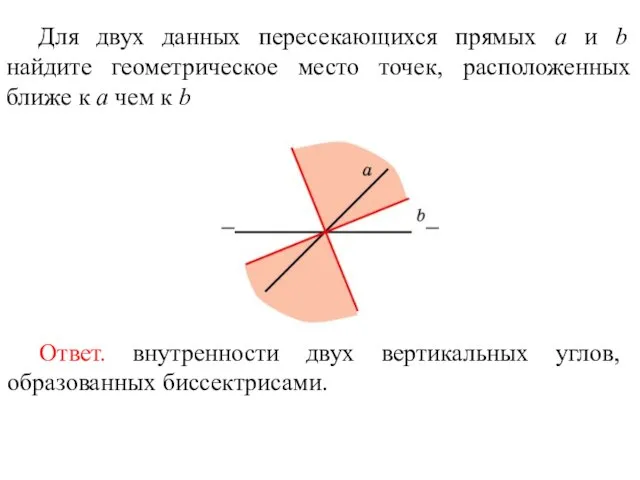
- 22. Для двух данных пересекающихся прямых a и b найдите геометрическое место точек, расположенных ближе к a
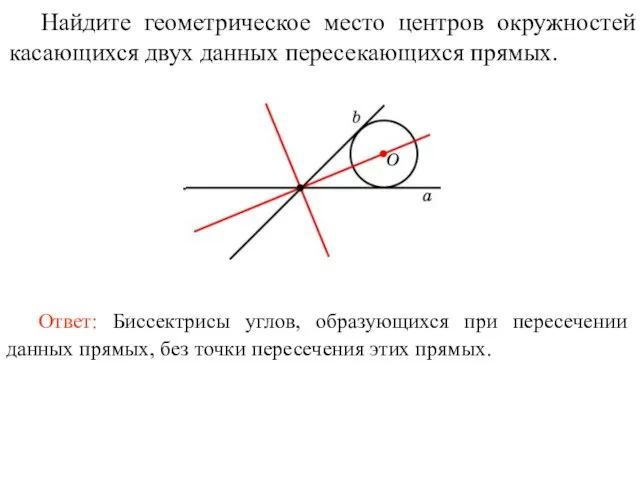
- 23. Найдите геометрическое место центров окружностей касающихся двух данных пересекающихся прямых.
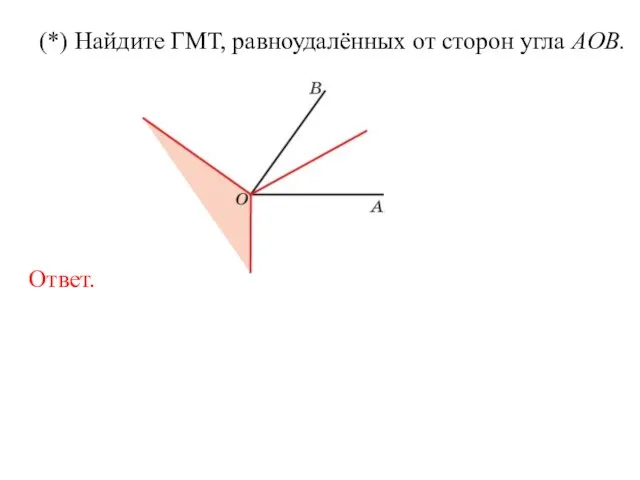
- 24. (*) Найдите ГМТ, равноудалённых от сторон угла AOB.
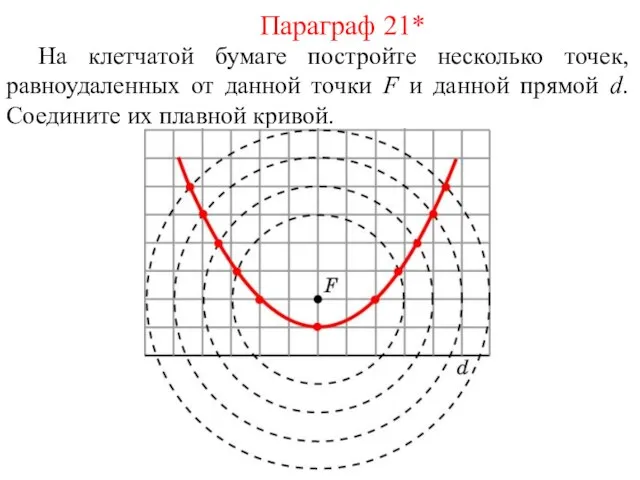
- 25. На клетчатой бумаге постройте несколько точек, равноудаленных от данной точки F и данной прямой d. Соедините
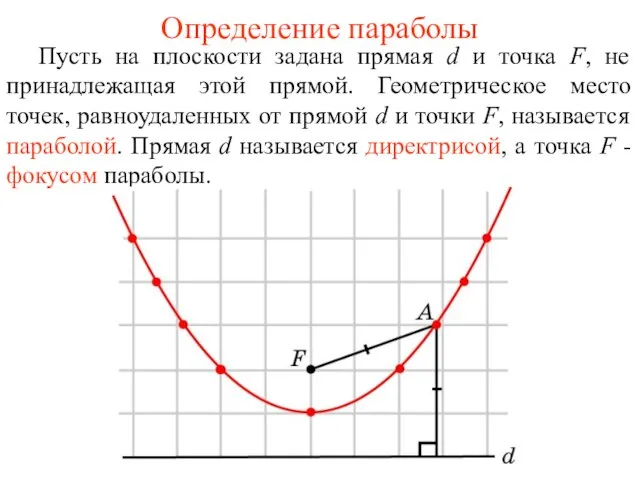
- 26. Определение параболы Пусть на плоскости задана прямая d и точка F, не принадлежащая этой прямой. Геометрическое
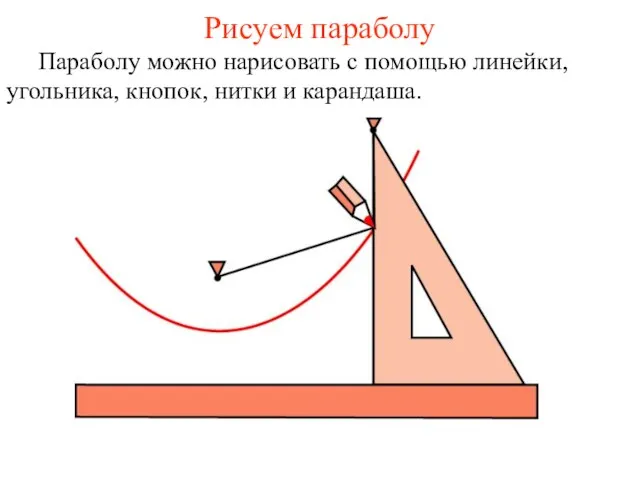
- 27. Рисуем параболу Параболу можно нарисовать с помощью линейки, угольника, кнопок, нитки и карандаша.
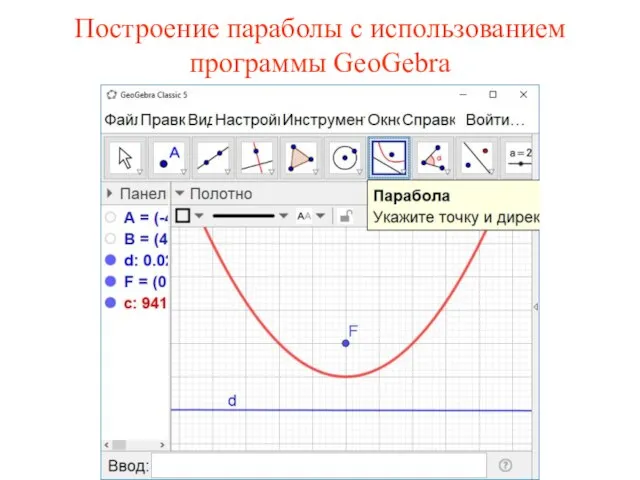
- 28. Построение параболы с использованием программы GeoGebra
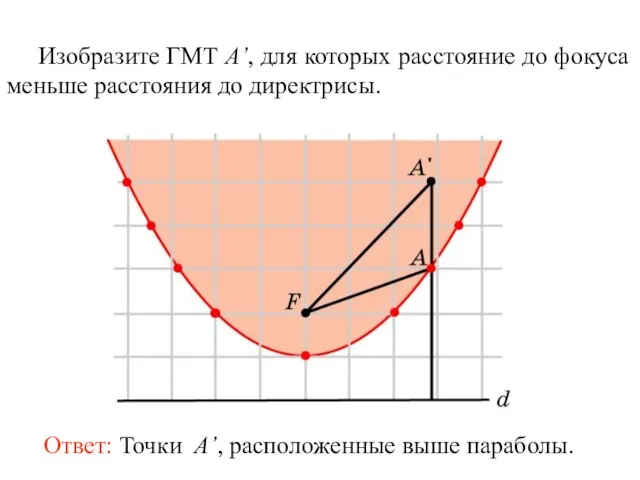
- 29. Изобразите ГМТ A’, для которых расстояние до фокуса меньше расстояния до директрисы.
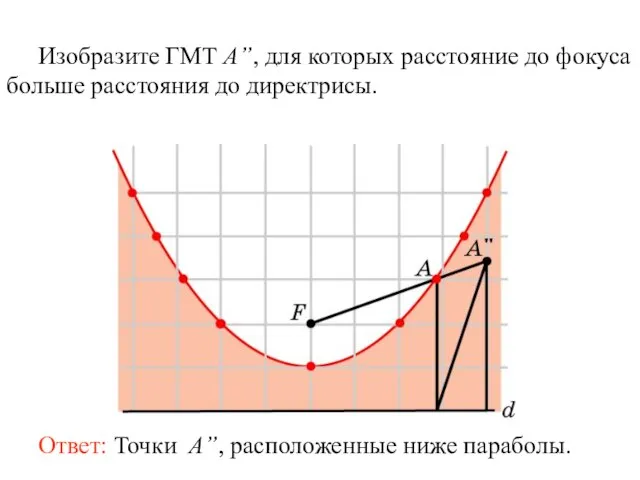
- 30. Изобразите ГМТ A”, для которых расстояние до фокуса больше расстояния до директрисы.
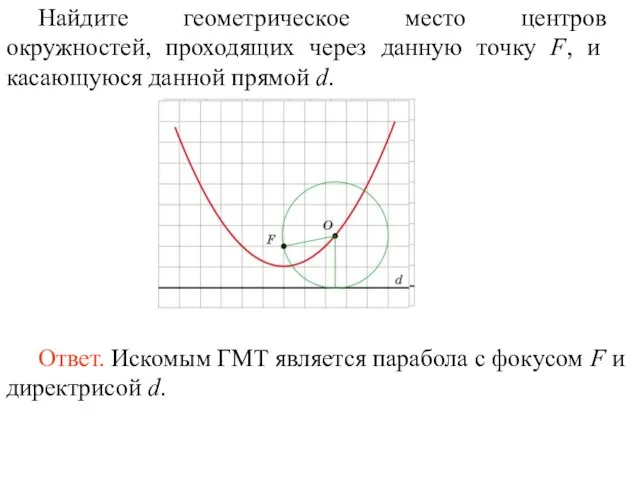
- 31. Найдите геометрическое место центров окружностей, проходящих через данную точку F, и касающуюся данной прямой d.
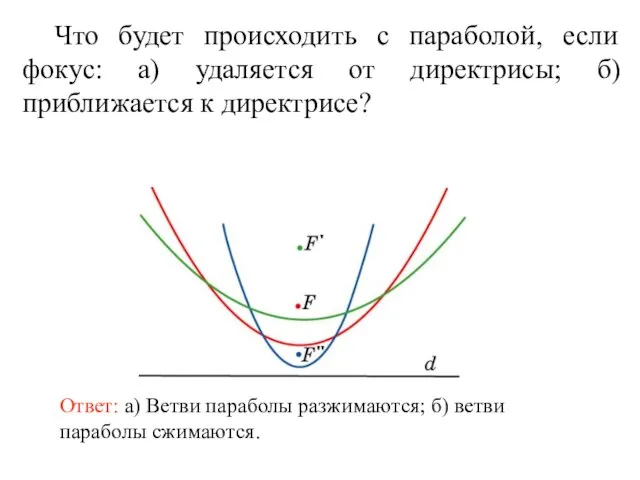
- 32. Что будет происходить с параболой, если фокус: а) удаляется от директрисы; б) приближается к директрисе?
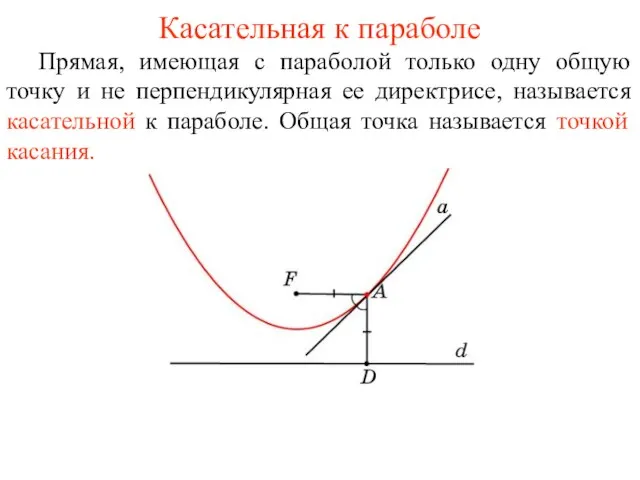
- 33. Касательная к параболе Прямая, имеющая с параболой только одну общую точку и не перпендикулярная ее директрисе,
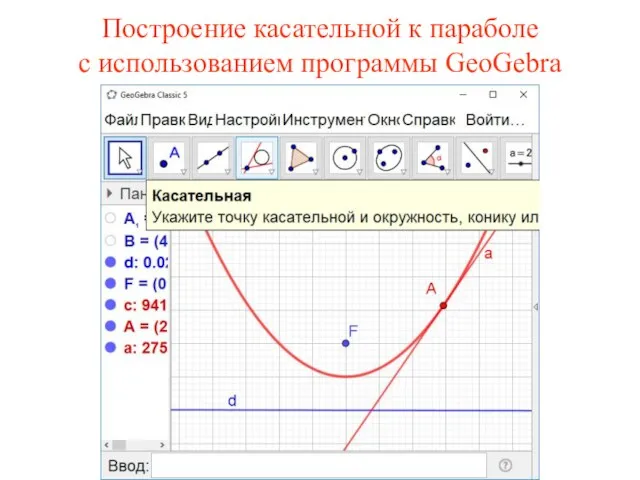
- 34. Построение касательной к параболе с использованием программы GeoGebra
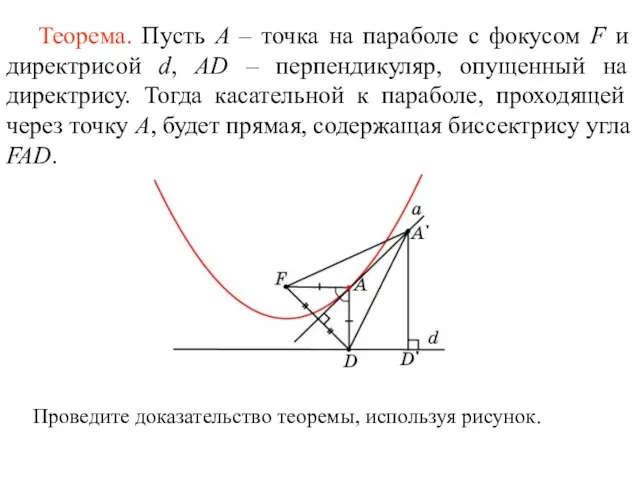
- 35. Теорема. Пусть A – точка на параболе с фокусом F и директрисой d, АD – перпендикуляр,
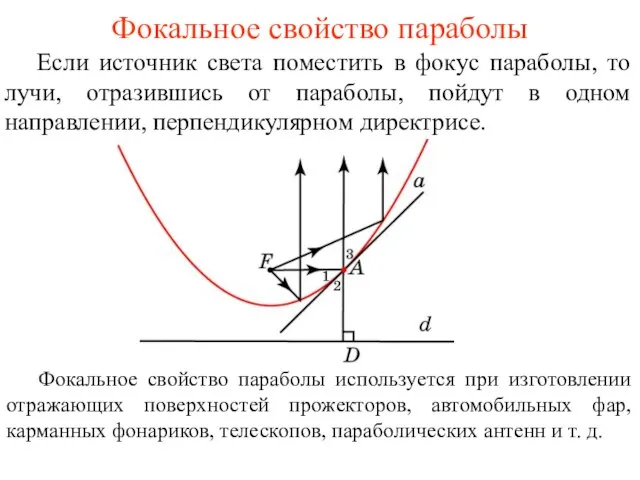
- 36. Фокальное свойство параболы Если источник света поместить в фокус параболы, то лучи, отразившись от параболы, пойдут
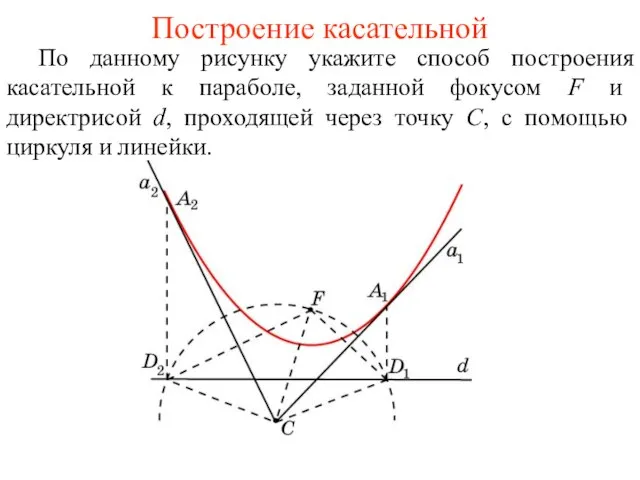
- 37. Построение касательной По данному рисунку укажите способ построения касательной к параболе, заданной фокусом F и директрисой
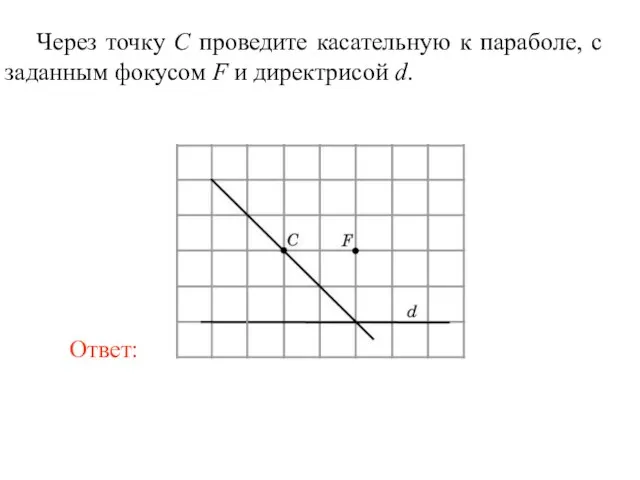
- 38. Через точку C проведите касательную к параболе, с заданным фокусом F и директрисой d.
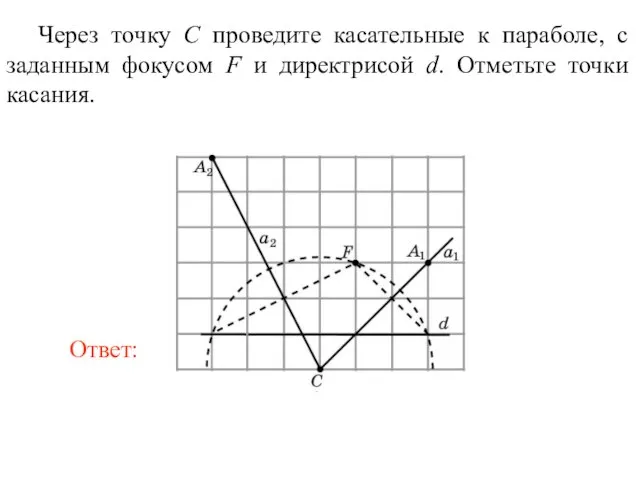
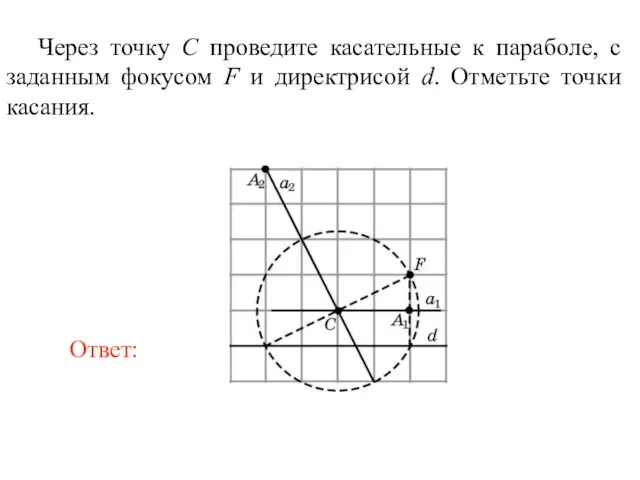
- 39. Через точку C проведите касательные к параболе, с заданным фокусом F и директрисой d. Отметьте точки
- 40. Через точку C проведите касательные к параболе, с заданным фокусом F и директрисой d. Отметьте точки
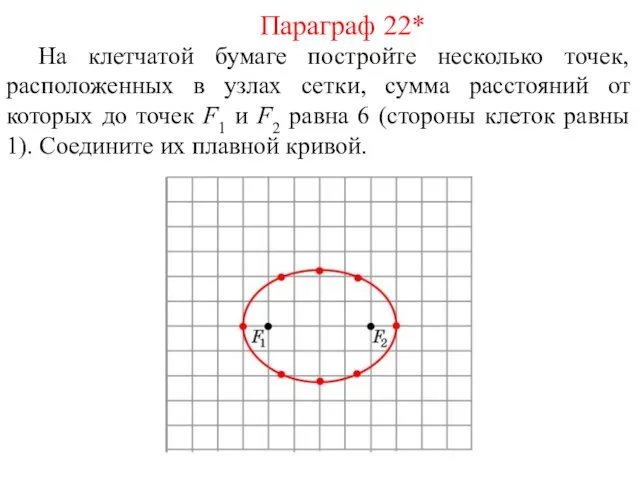
- 41. На клетчатой бумаге постройте несколько точек, расположенных в узлах сетки, сумма расстояний от которых до точек
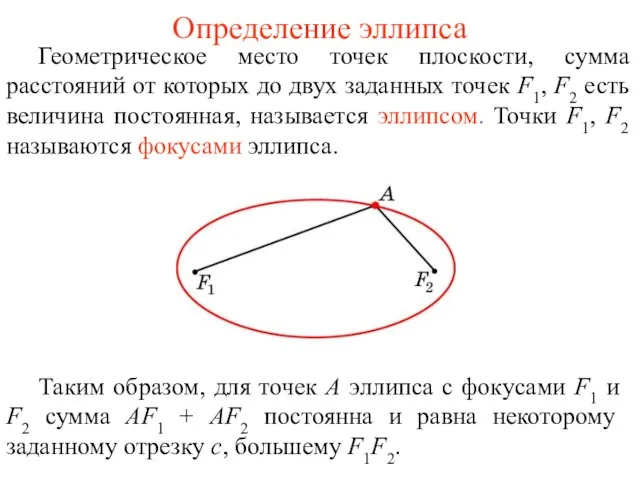
- 42. Определение эллипса Геометрическое место точек плоскости, сумма расстояний от которых до двух заданных точек F1, F2
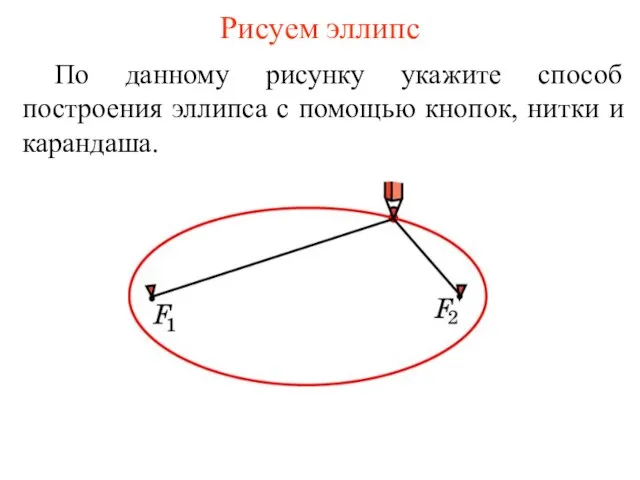
- 43. Рисуем эллипс По данному рисунку укажите способ построения эллипса с помощью кнопок, нитки и карандаша.
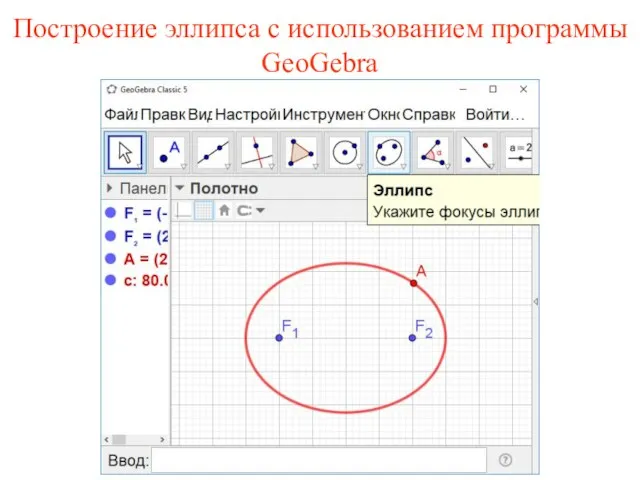
- 44. Построение эллипса с использованием программы GeoGebra
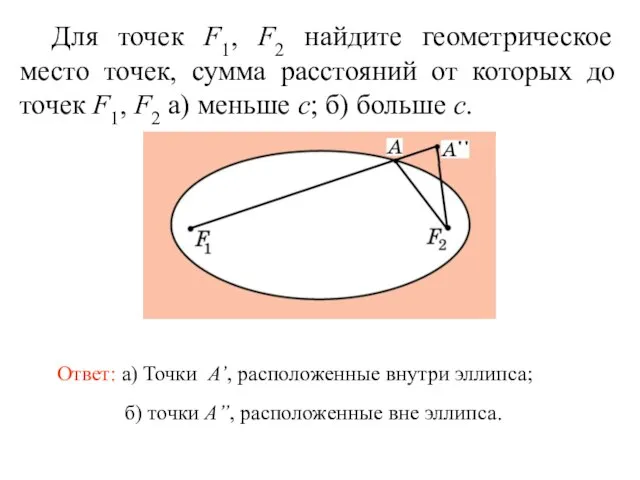
- 45. Для точек F1, F2 найдите геометрическое место точек, сумма расстояний от которых до точек F1, F2
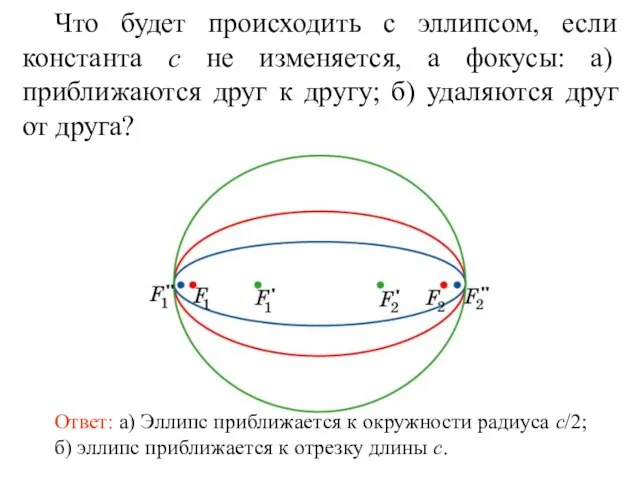
- 46. Что будет происходить с эллипсом, если константа c не изменяется, а фокусы: а) приближаются друг к
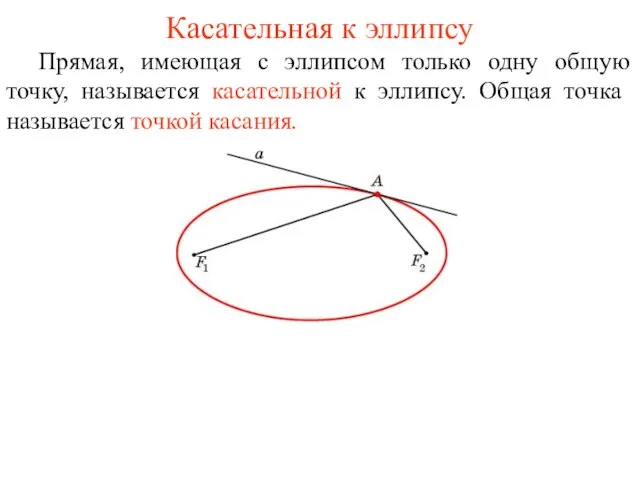
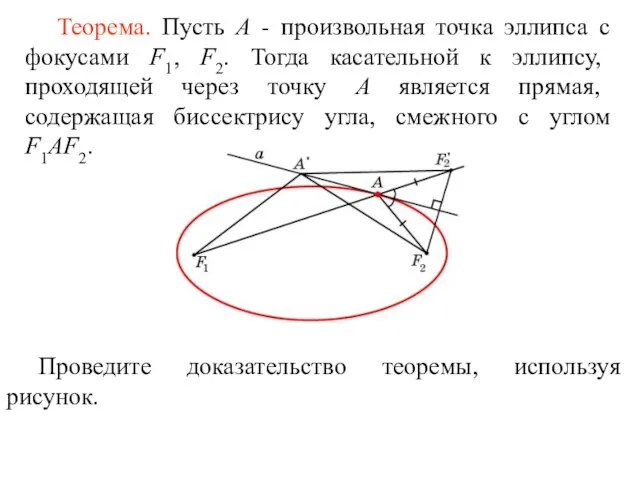
- 47. Касательная к эллипсу Прямая, имеющая с эллипсом только одну общую точку, называется касательной к эллипсу. Общая
- 48. Проведите доказательство теоремы, используя рисунок.
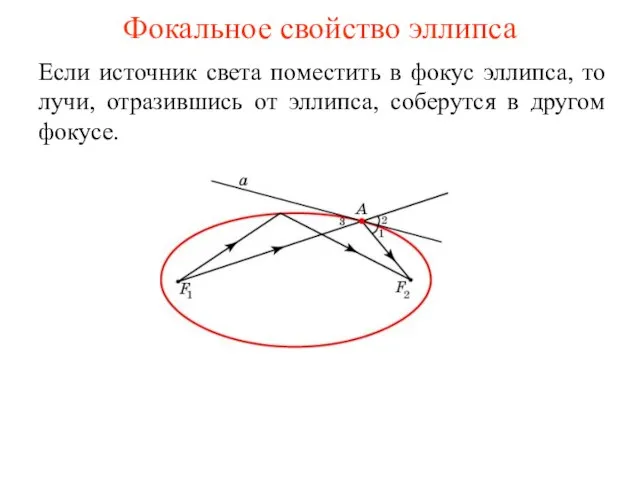
- 49. Фокальное свойство эллипса Если источник света поместить в фокус эллипса, то лучи, отразившись от эллипса, соберутся
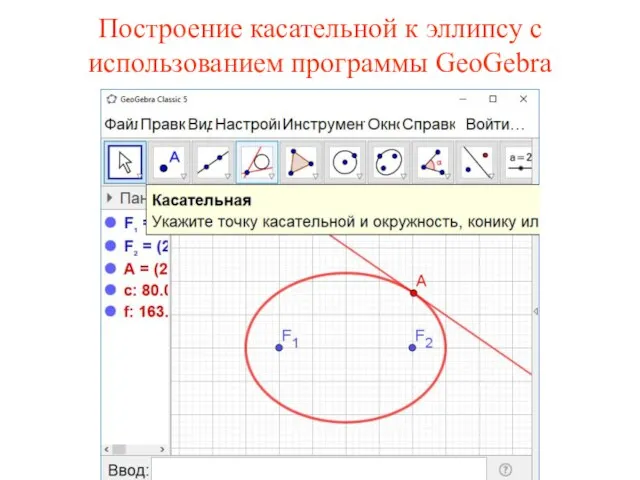
- 50. Построение касательной к эллипсу с использованием программы GeoGebra
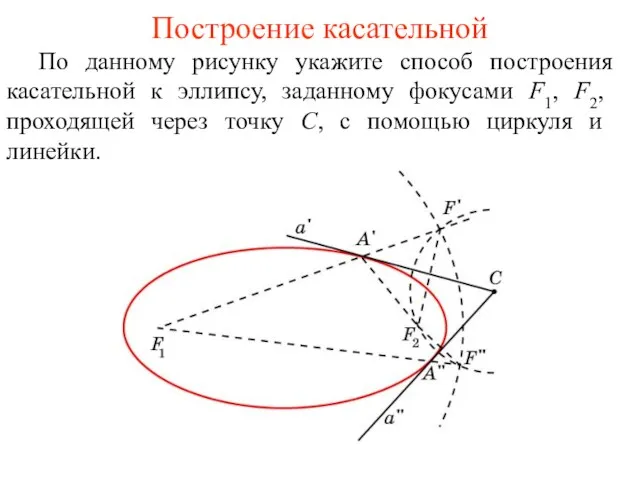
- 51. Построение касательной По данному рисунку укажите способ построения касательной к эллипсу, заданному фокусами F1, F2, проходящей
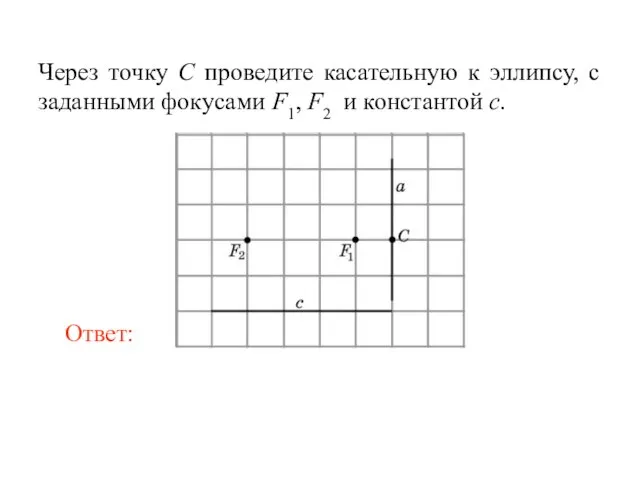
- 52. Через точку C проведите касательную к эллипсу, с заданными фокусами F1, F2 и константой с.
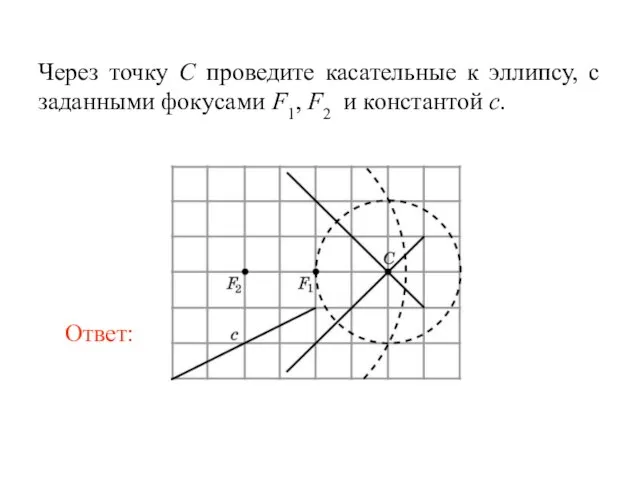
- 53. Через точку C проведите касательные к эллипсу, с заданными фокусами F1, F2 и константой с.
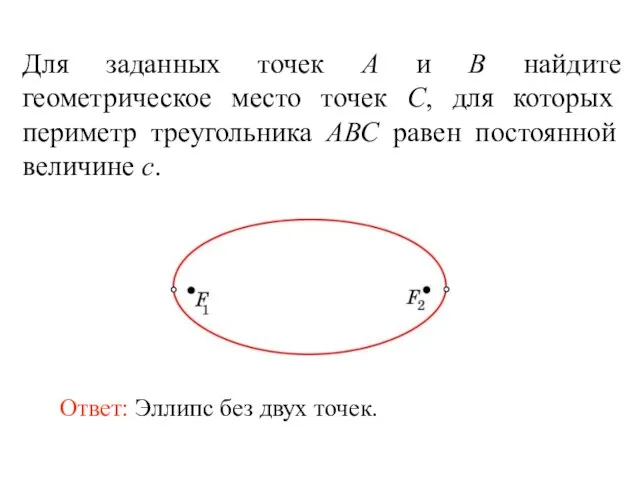
- 54. Для заданных точек А и В найдите геометрическое место точек С, для которых периметр треугольника АВС
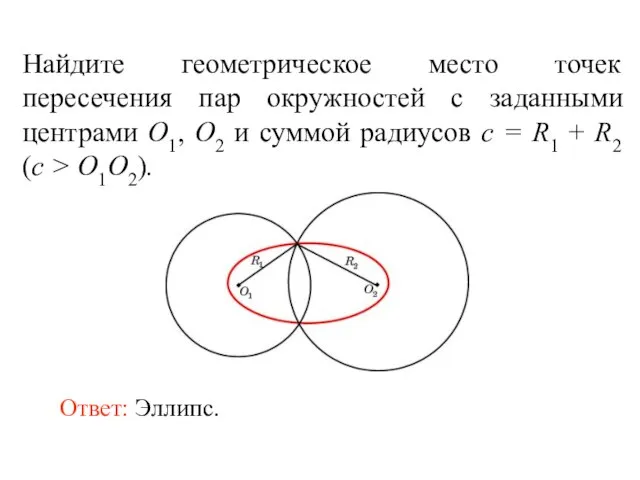
- 55. Найдите геометрическое место точек пересечения пар окружностей с заданными центрами O1, O2 и суммой радиусов c
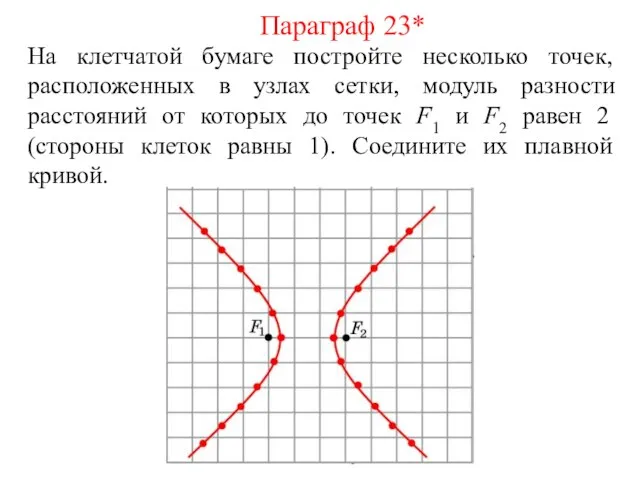
- 56. На клетчатой бумаге постройте несколько точек, расположенных в узлах сетки, модуль разности расстояний от которых до
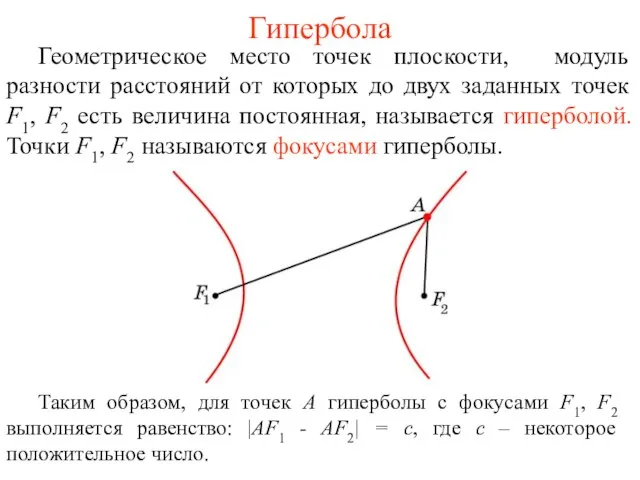
- 57. Гипербола Геометрическое место точек плоскости, модуль разности расстояний от которых до двух заданных точек F1, F2
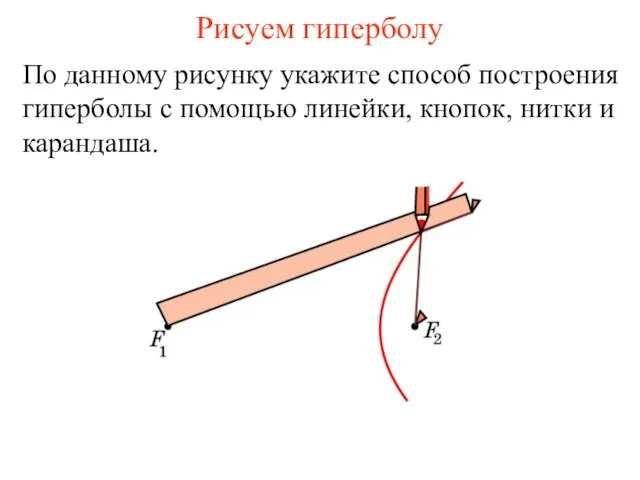
- 58. Рисуем гиперболу По данному рисунку укажите способ построения гиперболы с помощью линейки, кнопок, нитки и карандаша.
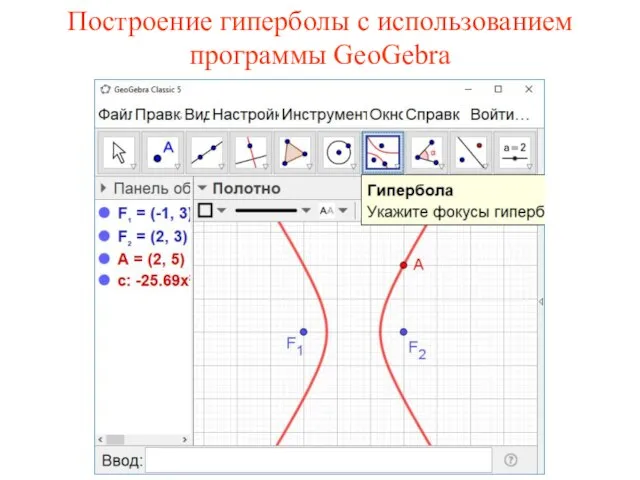
- 59. Построение гиперболы с использованием программы GeoGebra
- 60. Найдите геометрическое место точек A, для которых разность AF1 – AF2 расстояний до двух заданных точек
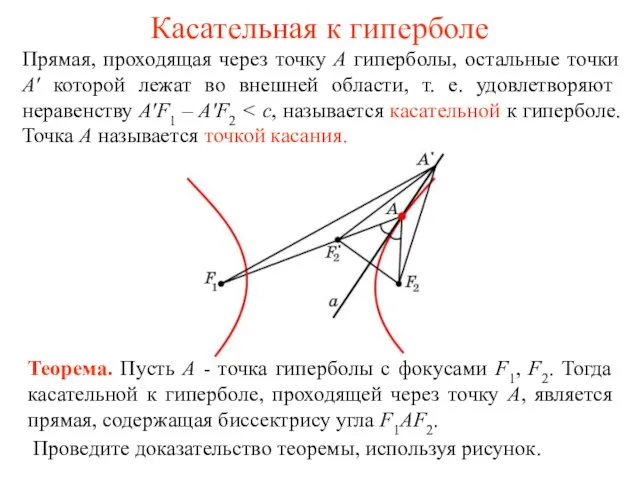
- 61. Касательная к гиперболе Прямая, проходящая через точку А гиперболы, остальные точки A' которой лежат во внешней
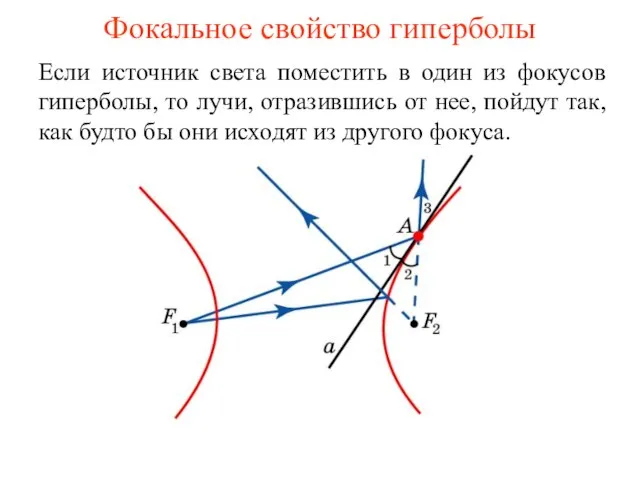
- 62. Фокальное свойство гиперболы Если источник света поместить в один из фокусов гиперболы, то лучи, отразившись от
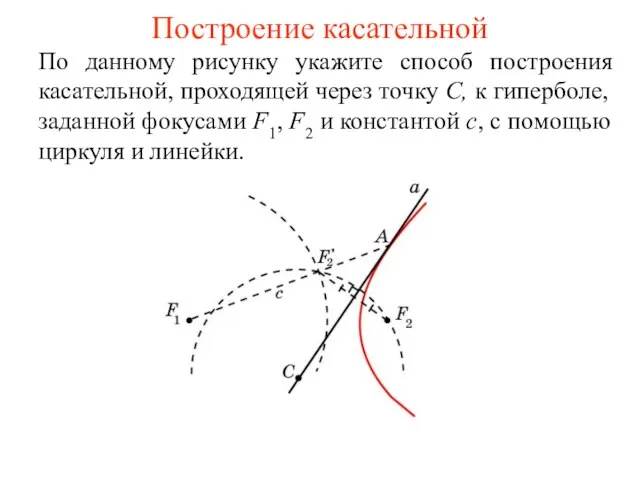
- 63. Построение касательной По данному рисунку укажите способ построения касательной, проходящей через точку C, к гиперболе, заданной
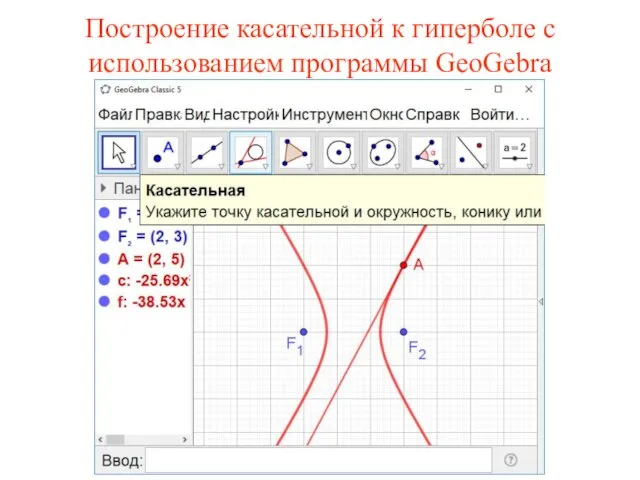
- 64. Построение касательной к гиперболе с использованием программы GeoGebra
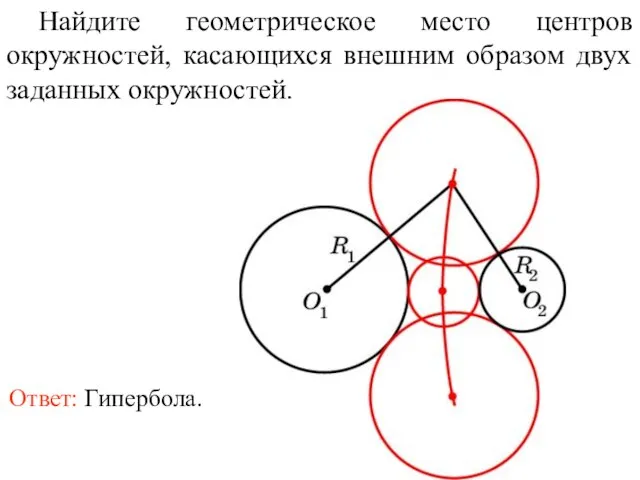
- 65. Найдите геометрическое место центров окружностей, касающихся внешним образом двух заданных окружностей.
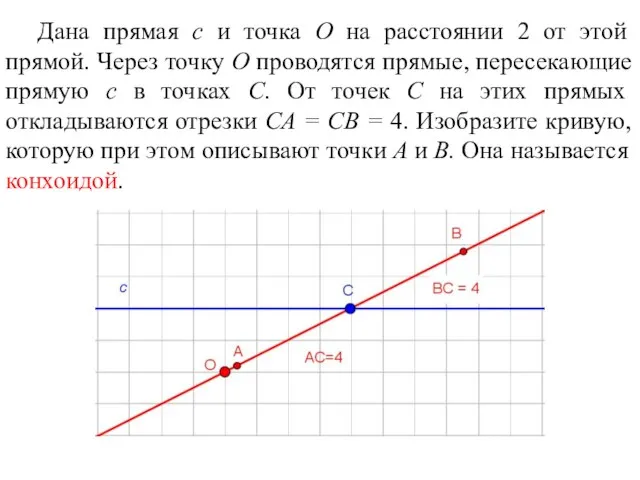
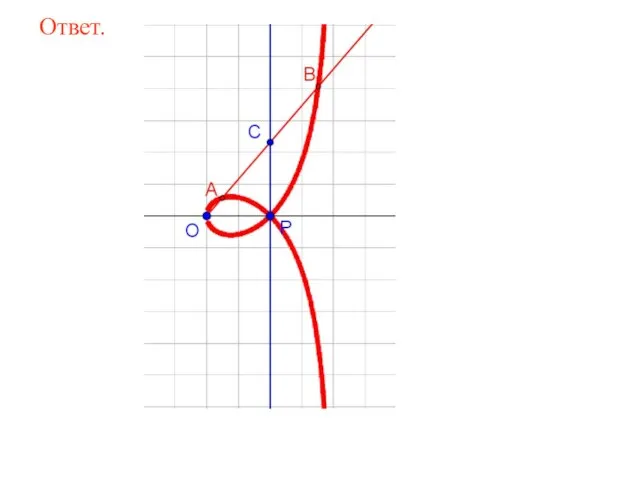
- 66. Дана прямая c и точка O на расстоянии 2 от этой прямой. Через точку O проводятся
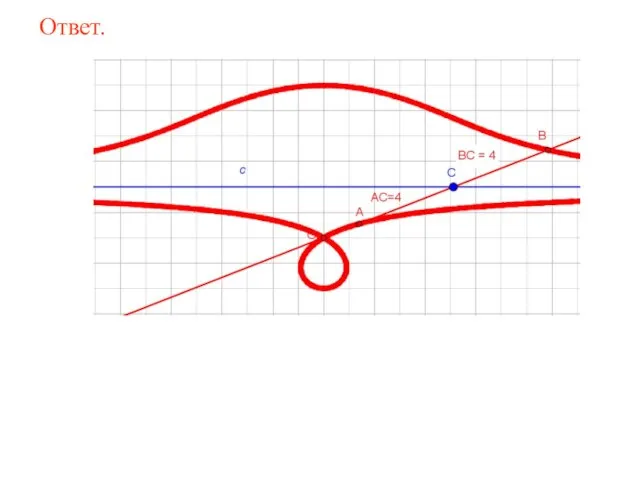
- 67. Ответ.
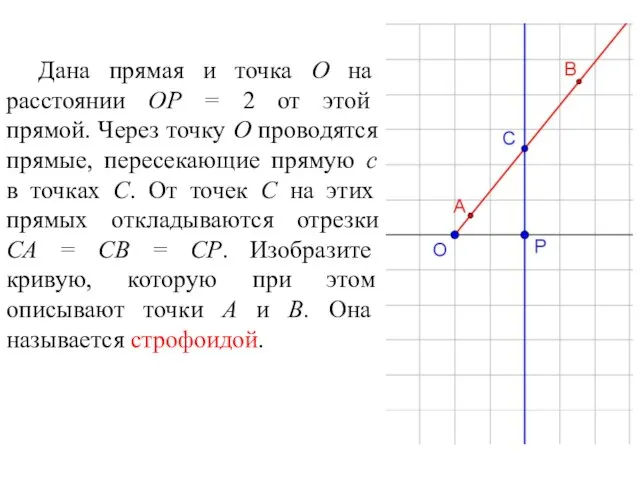
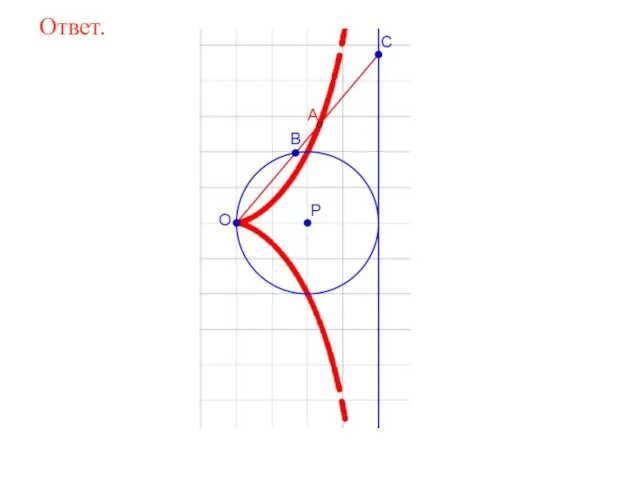
- 68. Дана прямая и точка O на расстоянии OP = 2 от этой прямой. Через точку O
- 69. Ответ.
- 70. Дана прямая и точка O на расстоянии OQ = 4 от этой прямой. С диаметром OQ
- 71. Ответ.
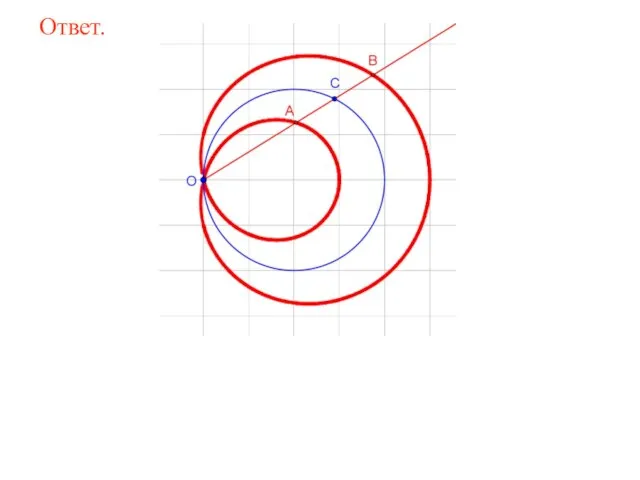
- 72. Дана окружность радиусом 2 и точка O, ей принадлежащая. Через точку O проводятся прямые, пересекающие окружность
- 73. Ответ.
- 75. Скачать презентацию













 Решение задач на движение в противоположных направлениях
Решение задач на движение в противоположных направлениях Подготовка к к/р
Подготовка к к/р Презентация по математике "Использование информационных технологий в преподавании математики" -
Презентация по математике "Использование информационных технологий в преподавании математики" -  История возникновения процентов
История возникновения процентов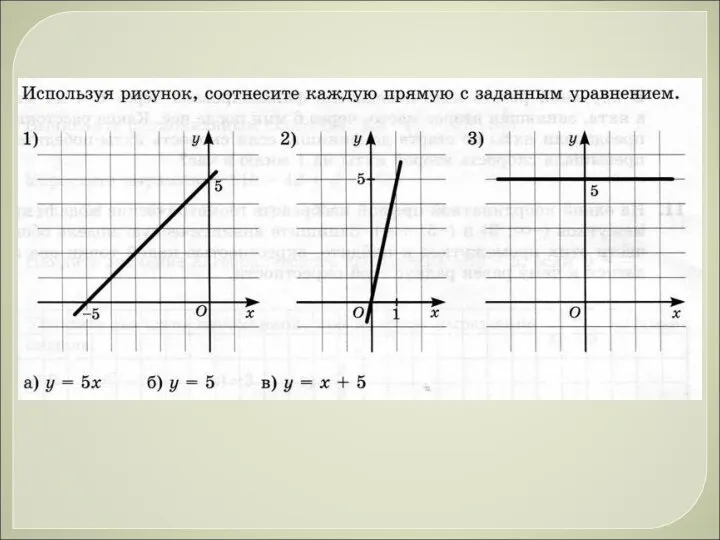 Соотношение прямой с заданным уравнением
Соотношение прямой с заданным уравнением Консультация к экзамену по математике в форме ЕГЭ. Задания В1 - В15
Консультация к экзамену по математике в форме ЕГЭ. Задания В1 - В15 Считаем в уме
Считаем в уме Равнобедренный треугольник
Равнобедренный треугольник Маршрутный лист группы
Маршрутный лист группы Презентация на тему Свойства функции
Презентация на тему Свойства функции  Число потоков в графе
Число потоков в графе Основные типы дифференциальных уравнений первого порядка
Основные типы дифференциальных уравнений первого порядка Транспортир Измерение углов Транспортир. История транспортира. Использование транспортира в жизни человека. Виды транспортир
Транспортир Измерение углов Транспортир. История транспортира. Использование транспортира в жизни человека. Виды транспортир Целые числа. Обзор и контроль
Целые числа. Обзор и контроль Скрещивающиеся прямые. Вопросы, задачи
Скрещивающиеся прямые. Вопросы, задачи Решение задач на дроби
Решение задач на дроби Координатные векторы
Координатные векторы Построение сечений тетраэдра и параллелепипеда
Построение сечений тетраэдра и параллелепипеда Математика. Основные понятия математики
Математика. Основные понятия математики Динамика системы вблизи цикла
Динамика системы вблизи цикла Правильные многогранники в представлении пяти стихий
Правильные многогранники в представлении пяти стихий Кривые второго порядка
Кривые второго порядка Разложение многочлена на множители. Работа над ошибками
Разложение многочлена на множители. Работа над ошибками Преобразование логарифмических выражений
Преобразование логарифмических выражений Квадратные уравнения
Квадратные уравнения Путешествие по родному краю. Курильский заповедник. Выбери наибольшее число
Путешествие по родному краю. Курильский заповедник. Выбери наибольшее число Второй признак равенства треугольников
Второй признак равенства треугольников Многогранники. Призма
Многогранники. Призма