Содержание
- 2. Изобретатель первых логарифмических таблиц, Непер, так говорил о своих побуждениях: «Я старался, насколько мог и умел,
- 3. Бригг осуществил свое намерение и направился в Шотландию, чтобы посетить изобретателя логарифмов. При встрече Бригг сказал:
- 4. О П Р Е Д Е Л Е Н И Е. Логарифмом числа b по основанию
- 5. Log 2 16; log 2 64; log 2 2; Log 2 1 ; log 2 (1/2);
- 6. Сравните со своими ответами ! Log 2 16; log 2 64; log 2 2; Log 2
- 7. 7 Правильное решение примеров 1 столбца: Log 2 16 = 4, так как 2 4 =
- 8. Определение логарифма можно записать так: a log a b = b Это равенство справедливо при b>0,
- 9. Таблица ответов: Если Вы выполнили всё правильно, перейдите к заданиям из учебника. Если выполнили с ошибками,
- 10. « СЧИТАЙ НЕСЧАСТНЫМ ТОТ ДЕНЬ ИЛИ ЧАС, В КОТОРЫЙ ТЫ НЕ УСВОИЛ НИЧЕГО НОВОГО И НИЧЕГО
- 12. Скачать презентацию









 Операции алгебры логики
Операции алгебры логики Решение задач с помощью уравнений. Урок математики в 5 классе
Решение задач с помощью уравнений. Урок математики в 5 классе Теория игр
Теория игр Равенство треугольников
Равенство треугольников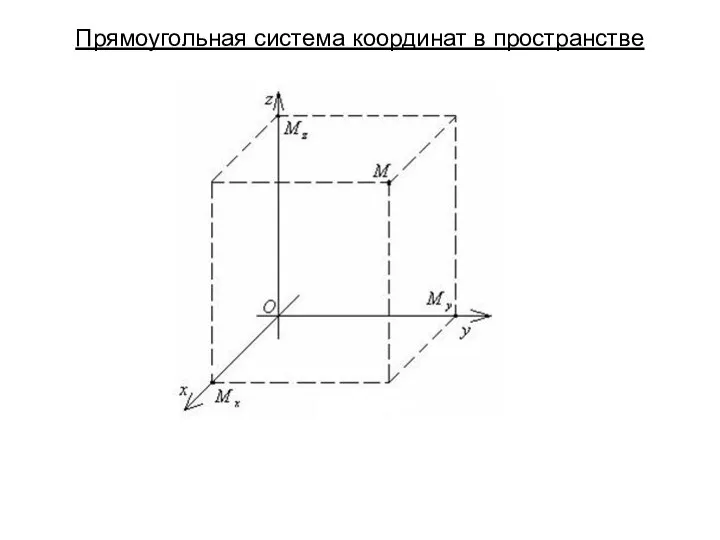 Прямоугольная система координат в пространстве. Понятие вектора
Прямоугольная система координат в пространстве. Понятие вектора Презентация на тему Квадрат суммы и квадрат разности (7 класс)
Презентация на тему Квадрат суммы и квадрат разности (7 класс)  Признаки существования предела
Признаки существования предела Площади фигур. 8 класс
Площади фигур. 8 класс Обобщение пропорции и лекарственные растения Сибири
Обобщение пропорции и лекарственные растения Сибири Презентация по математике "Письменные приёмы умножения" -
Презентация по математике "Письменные приёмы умножения" -  Анализ задач и альтернативные методы решений. Мастер-класс
Анализ задач и альтернативные методы решений. Мастер-класс Сложение чисел с разными знаками
Сложение чисел с разными знаками Обобщающий урок по начертательной геометрии прямая. Плоскость
Обобщающий урок по начертательной геометрии прямая. Плоскость Декартова система координат в пространстве
Декартова система координат в пространстве Луч. Дополнительные лучи. 5 класс
Луч. Дополнительные лучи. 5 класс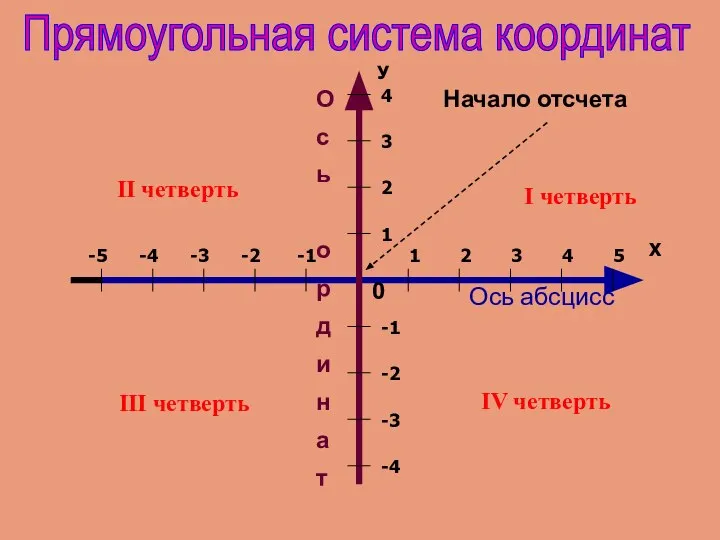 Ось абсцисс
Ось абсцисс Составление арифметических задач
Составление арифметических задач Алгоритм решения задач на нахождение слагаемых по сумме и разности
Алгоритм решения задач на нахождение слагаемых по сумме и разности Матрицы
Матрицы Декартова система координат на плоскости. Математика, 6 класс
Декартова система координат на плоскости. Математика, 6 класс Площадь круга и площадь кругового сегмента
Площадь круга и площадь кругового сегмента Решение задач по теме Объемы тел
Решение задач по теме Объемы тел Презентация на тему Геометрические построения в школьном курсе математики
Презентация на тему Геометрические построения в школьном курсе математики  Окружность
Окружность Через точку А провести профильную прямую ВС, равнонаклоненную к плоскости П1 и плоскости П2. (задача 20)
Через точку А провести профильную прямую ВС, равнонаклоненную к плоскости П1 и плоскости П2. (задача 20) Решение уравнений методом замены переменной
Решение уравнений методом замены переменной Презентация на тему Теоремы синусов и косинусов
Презентация на тему Теоремы синусов и косинусов  Свойства квадратных корней
Свойства квадратных корней