Логика и компьютер. Логические операции. Диаграммы Эйлера-Венна

Основоположники логики
Аристотель, в работах которого сформулированы понятия «суждение, умозаключение», начата разработка законов логики. Аристотелева логика считается классической, формальной логикой.
Большой вклад в развитие логики внес Лейбниц. В его время словесная форма записи стала неудобна для записи сложных выражений. Лейбниц придал логике символьный вид.
Алгебра логики, основы которой заложил в начале 19 века Дж. Буль, используется для решения задач, написания сложных программ.

Алгебра логики
Алгебра логики — это математический аппарат, с помощью которого записывают, вычисляют, упрощают и преобразовывают логические высказывания.
Создателем алгебры логики является живший в ХIХ веке английский математик Джордж Буль, в честь которого эта алгебра названа булевой алгеброй высказываний.

Логика (древнегреч. - слово, мысль, понятие, рассуждение) - наука о законах и формах мышления(понятие, высказывание, умозаключение.
Алгебра логики изучает общие операции над высказываниями.

ЧТО ИЗУЧАЕТ ШКОЛЬНАЯ АЛГЕБРА

Высказывание (суждение) - это повествовательное предложение, в котором что-либо утверждается или отрицается. По поводу любого высказывания можно сказать истинно оно или ложно.

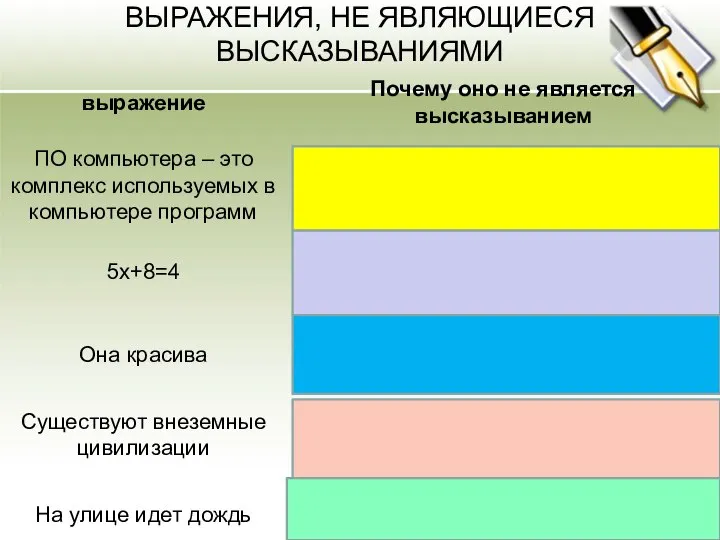
ВЫРАЖЕНИЯ, НЕ ЯВЛЯЮЩИЕСЯ ВЫСКАЗЫВАНИЯМИ

В алгебре логики высказывания
обозначаются именами
логических переменных (А, В,
С), которые могут принимать
значения истина (1) или ложь (0).
Истина, ложь – логические константы.

Что изучает алгебра логики

Примеры высказываний:
Город Вашингтон – столица США. (истинное)
Число 2 является делителем числа 7. (ложное)

Какие из предложений являются высказываниями? Если являются, то истинными или ложными?
Число 6 – четное.
Посмотрите на доску.
Внимание!
х > 0.
Некоторые люди являются художниками.
Память компьютера – совокупность устройств для хранения информации.
Наполеон был английским императором.
Все ребята умеют плавать.
Каждый человек – художник.
Н + Н + О = Н2О
Да1
Нет
Нет
Нет
Да1
Нет
Да0
Да0
Да0
Да1

Логическое выражение – простое или сложное высказывание. Сложное высказывание строится из простых с помощью логических операции.

ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ.

Булева алгебра.
Булева алгебра состоит из компонентов:
Логические объекты ( выражения)
Операции над логическими объектами
Аксиомы и теоремы, регламентирующие эти
операции

Высказывание может принимать одно из двух возможных логических значений: ИСТИНА или ЛОЖЬ
ИСТИНА
ЛОЖЬ
ЛОГИЧЕСКИЕ ПОСТОЯННЫЕ
Или
ЛОГИЧЕСКИЕ КОНСТАНТЫ

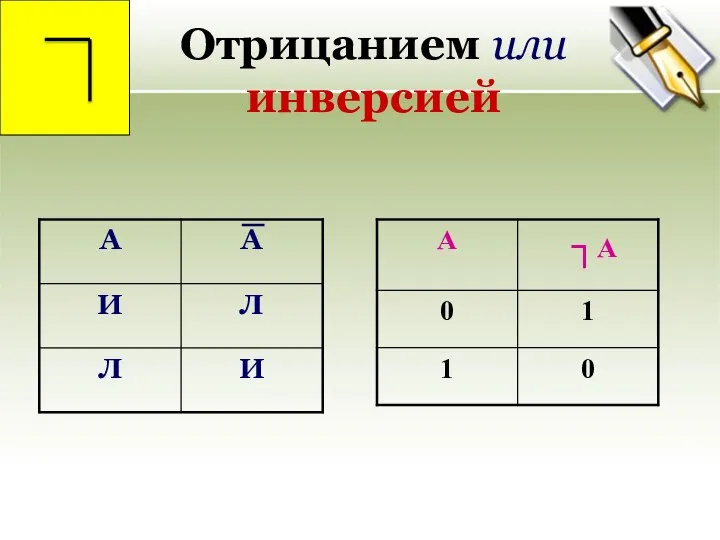
ЛОГИЧЕСКИЕ ОПЕРАЦИИ:
Отрицанием, или инверсией высказывания А называется новое высказывание А, которое истинно тогда, когда А – ложно, и ложно тогда, когда А – истинно.
Отрицание, или инверсия
«НЕ», «НЕВЕРНО, ЧТО»
NOT

Отрицанием или инверсией

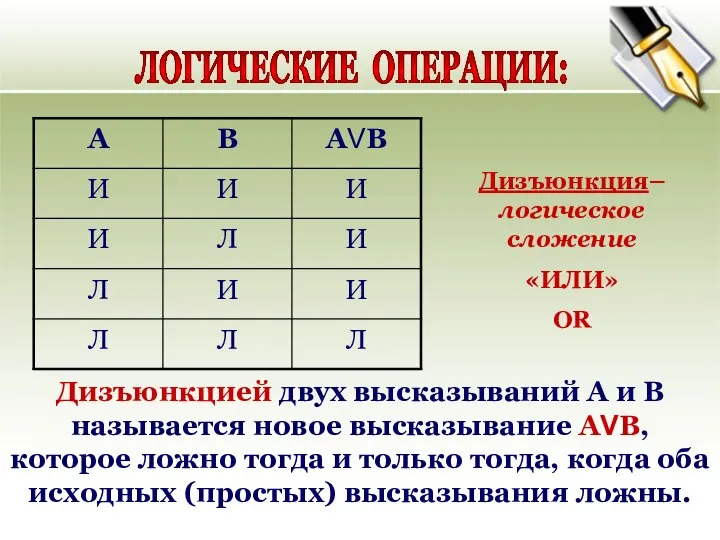
ЛОГИЧЕСКИЕ ОПЕРАЦИИ:
Дизъюнкцией двух высказываний А и В называется новое высказывание АVВ, которое ложно тогда и только тогда, когда оба исходных (простых) высказывания ложны.
Дизъюнкция– логическое сложение
«ИЛИ»
OR

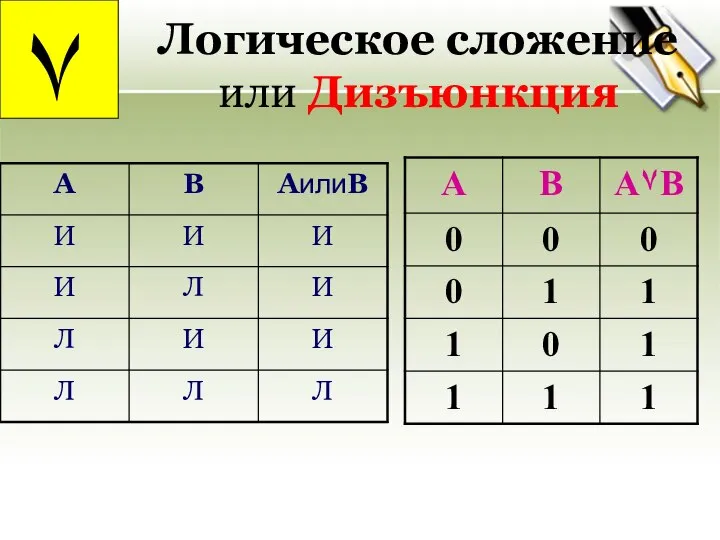
Логическое сложение или Дизъюнкция
۷

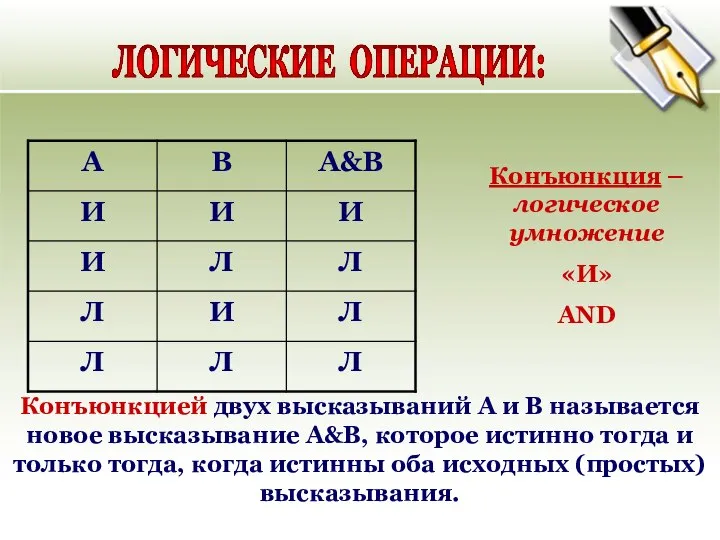
ЛОГИЧЕСКИЕ ОПЕРАЦИИ:
Конъюнкцией двух высказываний А и В называется новое высказывание А&В, которое истинно тогда и только тогда, когда истинны оба исходных (простых) высказывания.
Конъюнкция – логическое умножение
«И»
AND

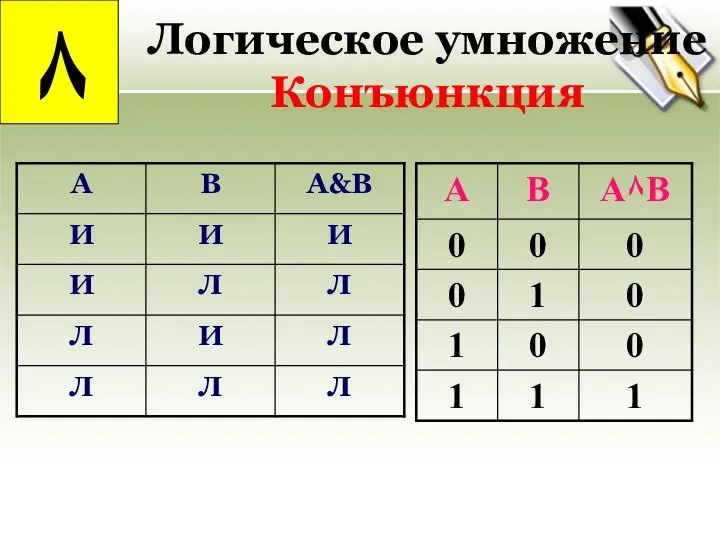
Логическое умножение Конъюнкция
٨

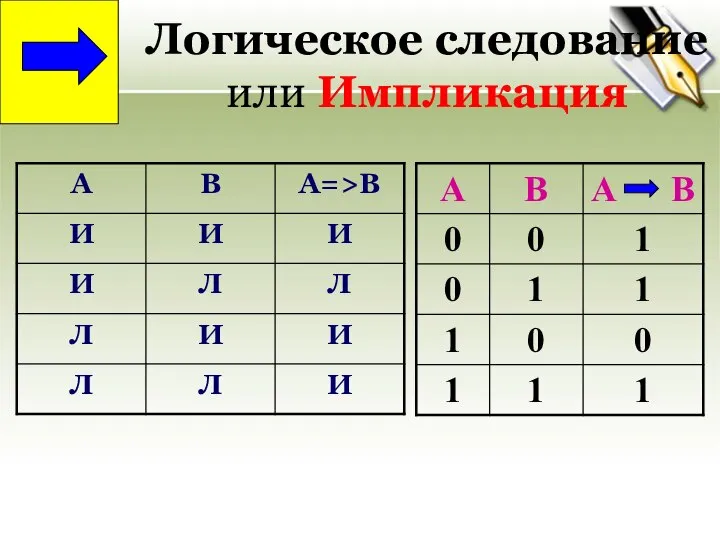
ЛОГИЧЕСКИЕ ОПЕРАЦИИ:
Импликация -- связывает два простых логических высказывания, из которых первое (А) является условием, а второе (В) – следствием. Результатом импликации является ЛОЖЬ тогда и только тогда, когда условие (А) истинно, а следствие (В) ложно.
Импликация – логическое следование
«ЕСЛИ… , ТО…»

Логическое следование или Импликация

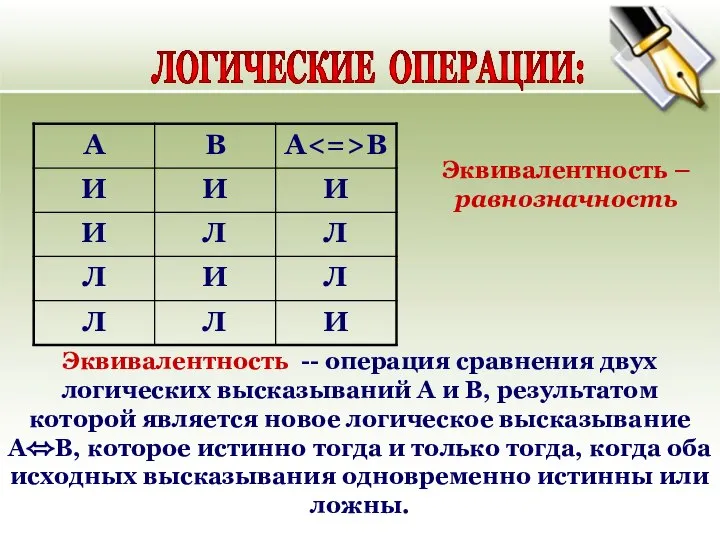
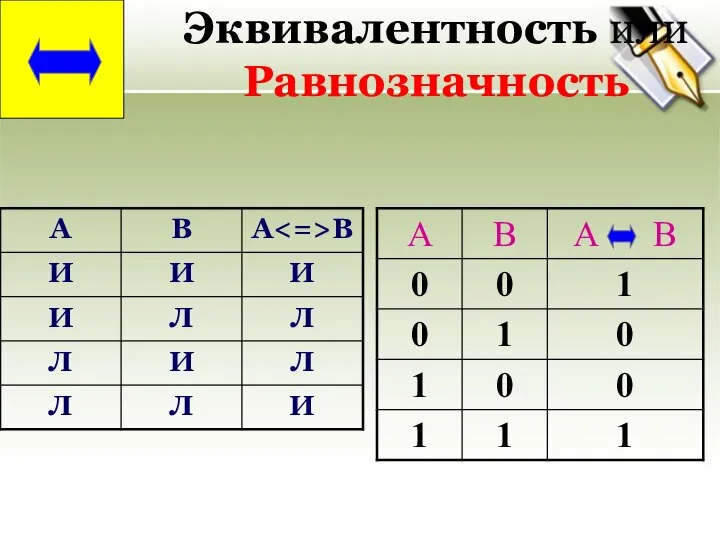
ЛОГИЧЕСКИЕ ОПЕРАЦИИ:
Эквивалентность -- операция сравнения двух логических высказываний А и В, результатом которой является новое логическое высказывание А⬄В, которое истинно тогда и только тогда, когда оба исходных высказывания одновременно истинны или ложны.
Эквивалентность – равнозначность

Эквивалентность или Равнозначность

Порядок выполнения логических операций.
1. Инверсия - ┐
2. Конъюнкция - & или ٨
3. Дизъюнкция – ۷
4. Импликация –
5. Эквивалентность -
Для изменения указанного порядка выполнения логических операций используются круглые скобки.
Например: D = ┐( A ۷ B ٨ C)

РЕШЕНИЕ ЗАДАЧ

Вычислить значение логической формулы:
¬ Х &У Х &Z,
если логические переменные имеют следующие значения:
Х=0, У=1, Z=1

Из двух простых высказываний постройте сложное высказывание, используя логические операции И, ИЛИ.
Все ученики изучают математику. Все ученики изучают литературу.
Все ученики изучают математику и литературу.
X>=3.
5>=3, 8>=3
Синий кубик меньше красного. Синий меньше зеленого.
В кабинете есть учебники. В кабинете есть справочники.

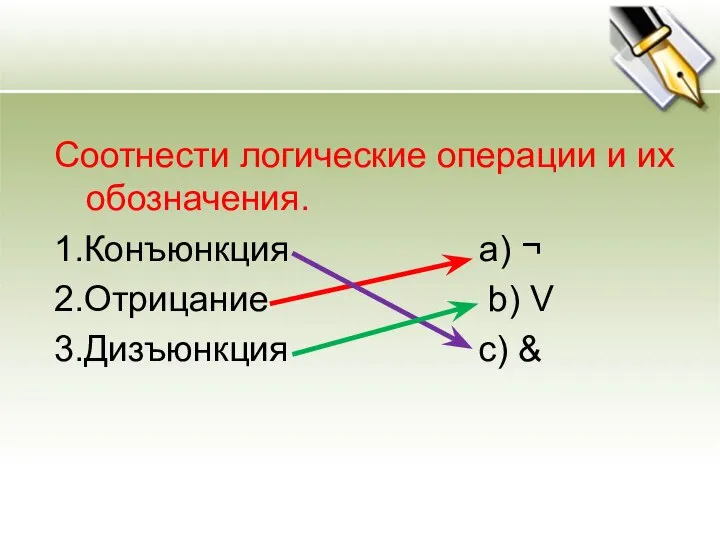
Соотнести логические операции и их обозначения.
1.Конъюнкция a) ¬
2.Отрицание b) V
3.Дизъюнкция c) &

Расположите правильно последовательность выполнения операций:
& , V, ¬
2 3 1