Математический анализ. Исследование функций и построение графиков. Асимптоты графика функции

1 семестр
Раздел 1. Введение в математический анализ.
Раздел 2. Дифференциальное исчисление функции одной переменной.
Раздел 3. Применение производных к исследованию функций.
Раздел 4. Неопределенный интеграл.

Исследование функций и построение графиков.
Асимптоты графика функции.
Общая схема исследования функции и построения графика.

Общая схема исследования функции и построения графика
Для построения графика дважды дифференцируемой (кроме, может быть, отдельных точек) функции будем придерживаться следующей схемы. Подобные схемы могут отличаться в деталях, но не в основных параметрах.

Область определения функции, четность, точки пересечения с осями координат, интервалы знакопостоянства.
Пределы на границе области определения.
Асимптоты.
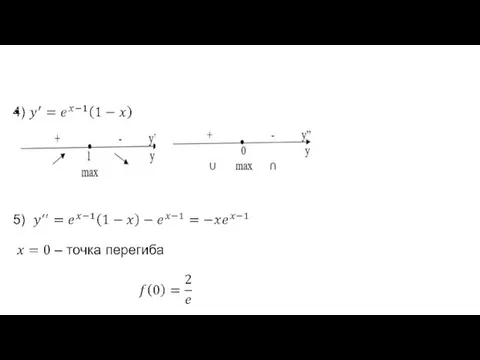
Монотонность и точки экстремума.
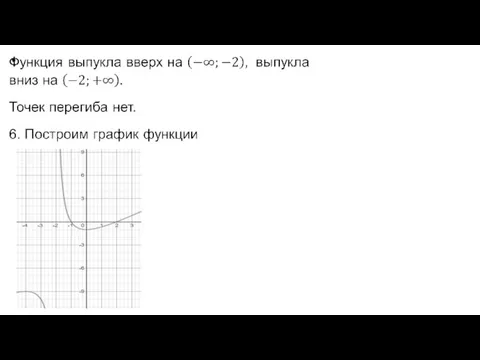
Выпуклость и точки перегиба.
График (с учетом результатов предыдущих пунктов).