Теория вероятностей. Случайные события

СЛУЧАЙНЫЕ СОБЫТИЯ

Основным понятием теории вероятностей является понятие случайного события.
Под событием понимается явление, которое происходит в результате осуществления некоторого набора условий. Осуществление какого-либо набора условий называется опытом или испытанием.
Случайным событием называется такое событие, которое может произойти или не произойти в результате опыта.

Опыт – бросание монеты.
События: появление «герба»,
появление « цифры».
Опыт – стрельба по мишени.
Событие – результаты стрельбы
(число очков).
Опыт – бросание игральной кости.
Событие - выпадение числа очков
(от 1 до 6).

Событие называется достоверным (U),
если оно обязательно произойдет в результате
испытания.
Событие называется невозможным или недостоверным (V), если оно не может произойти
в результате испытания.

Если в результате испытания появление
одного события исключает появление другого, то такие события называются несовместными.
Примеры:
Выпадение герба при одном бросании монеты
исключает появление цифры.
Выпадение «6» очков на игральной кости
исключает появление «3» очков.

События называются совместными, если в
результате одного опыта появление одного события не исключает появление другого.
Опыт – выбор карты из колоды.
События:
А – выбор туза,
В – выбор красной масти.
А и В – совместные события.

Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них.
Каждое событие из полной группы попарно несовместных событий называют исходами или элементарными событиями.
События называются равновозможными, если
в условиях опыта нет оснований считать какое-либо из них более возможным, чем любое другое.
Появление 1, 2, 3, 4, 5, 6 очков при бросании игральной кости образуют полную группу и являются равновозможными.

ОПРЕДЕЛЕНИЕ:
Суммой событий называется событие, состоящее в появлении одного из этих событий
А+В = А или В
АЛГЕБРА СОБЫТИЙ
ОПРЕДЕЛЕНИЕ:
Произведением событий называется событие, состоящее в одновременном появлении этих событий
А В = А и В

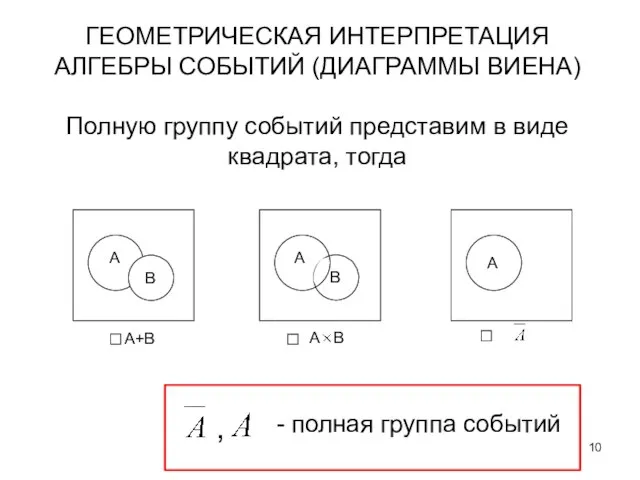
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
АЛГЕБРЫ СОБЫТИЙ (ДИАГРАММЫ ВИЕНА)
Полную группу событий представим в виде квадрата, тогда

Задача.
Бросается игральная кость
Обозначим события
А1 – выпало «2»
А2 – выпало «4»
А3 – выпало «6»
Записать:
выпало четное
А1+А2+А3

Задача.
Бросается игральная кость
Обозначим события
А1 – выпало более трех
А2 – выпало четное
Записать:
выпало «5»

КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ СОБЫТИЯ
ВЕРОЯТНОСТЬ СОБЫТИЯ А:
где
m – число благоприятных исходов;
n – общее число исходов.
Вероятность события – это численная мера объективной возможности его появления.

Задача.
Бросается игральная кость.
Найти вероятности событий:
1) выпало «3»
P(A)=1/6
2) выпало четное число больше двух
P(A)=2/6=1/3
3) выпало менее десяти очков
P(A)=6/6=1 (событие достоверное)
4) выпало более десяти очков
P(A)=0/6=0 (событие недостоверное)

Вероятность достоверного события равна 1.
Вероятность недостоверного события равна 0.
Свойства вероятности:

Относительной частотой появления события
понимается отношение числа опытов, в которых
появилось событие А, к числу всех опытов.
СТАТИСТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ СОБЫТИЯ

Бернулли доказал, что при неограниченном увеличении числа опытов относительная частота появления события будет сколь угодно мало отличаться от постоянного числа, которое и принимается за вероятность
события в отдельном опыте.
Поэтому относительную частоту появления события при достаточно большом числе опытов называют статистической вероятностью.
Яков Бернулли
XVII в.

Статистической вероятностью события А называется число, относительно которого стабилизируется относительная частота события А при неограниченном увеличении числа испытаний.

Задача.
Посажено 15 деревьев, из которых прижились 12.
Найти относительную частоту приживаемости.

ФОРМУЛЫ
КОМБИНАТОРИКИ

ОСНОВНОЕ ПРАВИЛО КОМБИНАТОРИКИ
Пусть требуется выполнить одно за другим k действий. Первое действие можно выполнить n1 способами, второе – n2 способами,…, k-тое действие – nk способами.
Тогда все k действий могут быть выполнены
способами.

Размещениями из n различных элементов по m элементов (m из данных n элементов по m элементов, отличающиеся либо самими элементами, либо порядком элементов.
Число размещений из n по m

Перестановками из n различных элементов называют размещения из n элементов по n элементов.
Число перестановок

Сочетаниями из n различных элементов по m элементов (m из данных n элементов по m элементов, отличающиеся хотя бы одним элементом. (Порядок элементов не учитывается)
Число сочетаний из n по m

Задача.
Сколькими способами из 20 присяжных заседателей можно отобрать троих для участия в судебном процессе.

Задача.
Сколькими способами из 20 членов правления можно отобрать троих для замещения вакансий вице-президентов, отвечающих соответственно за производство, финансы, реализацию продукции.

Задача.
Сколько четырехзначных чисел можно составить из цифр 1, 2, 3 и 4 с использованием всех указанных цифр в этом числе.

Задача.
Бросаются две игральные кости. Какова вероятность того, что сумма выпавших очков равна 7?

Задача.
Бросаются две игральные кости. Какова вероятность того, что произведение выпавших очков не равно 6?

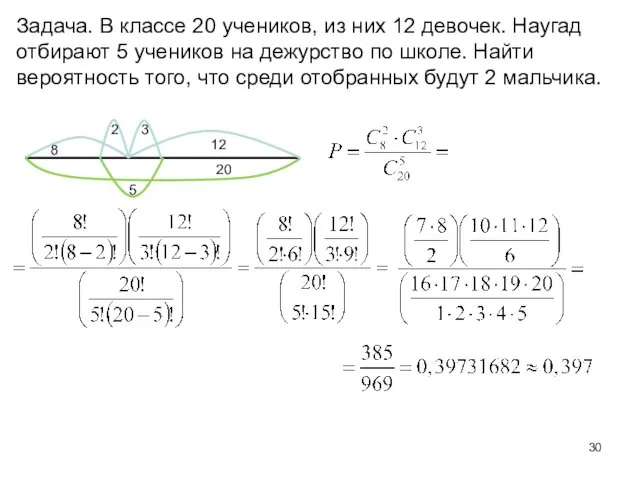
Задача. В классе 20 учеников, из них 12 девочек. Наугад отбирают 5 учеников на дежурство по школе. Найти вероятность того, что среди отобранных будут 2 мальчика.
20
12
2
8
5
3

ГЕОМЕТРИЧЕСКАЯ ВЕРОЯТНОСТЬ
Отрезок длины l составляет часть отрезка длины L. Вероятность попадания точки на отрезок длины l не зависит от его расположения и вычисляется по формуле
Классическое определение вероятности применимо лишь к конечному числу опытов.
В тех случаях, когда число опытов бесконечно, применяют геометрическую вероятность – вероятность попадания точки в область.

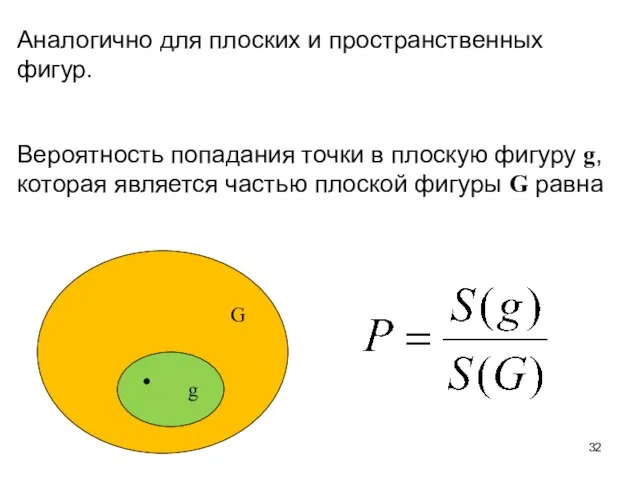
Аналогично для плоских и пространственных фигур.
Вероятность попадания точки в плоскую фигуру g, которая является частью плоской фигуры G равна

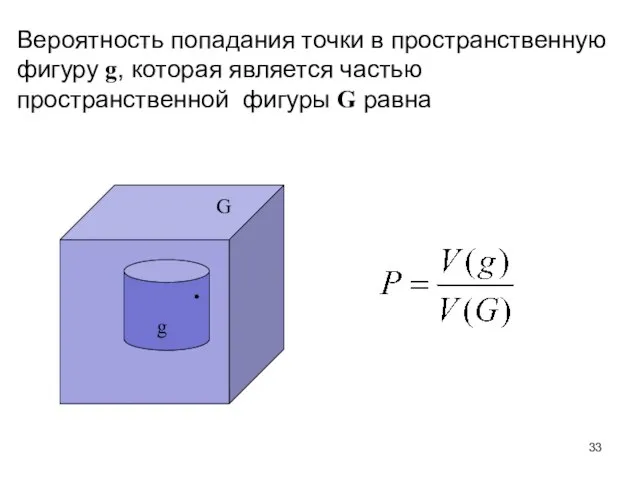
Вероятность попадания точки в пространственную фигуру g, которая является частью пространственной фигуры G равна
G
g