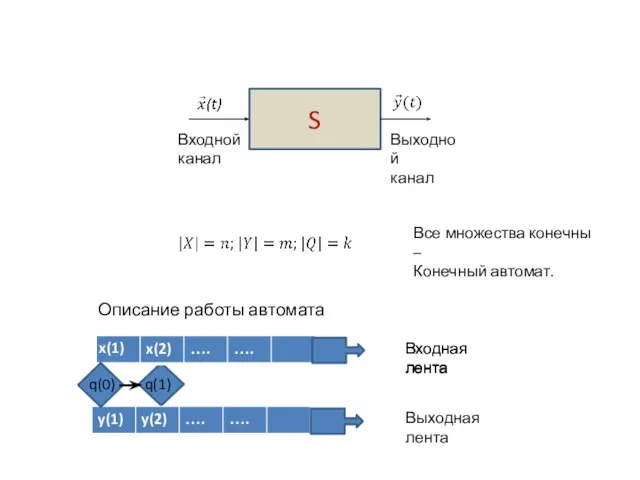
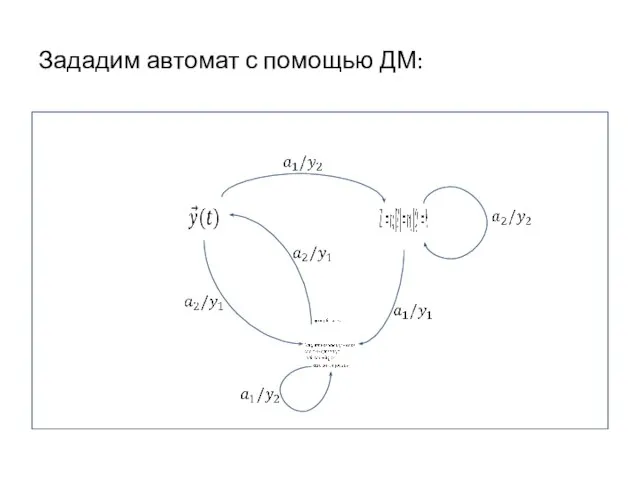
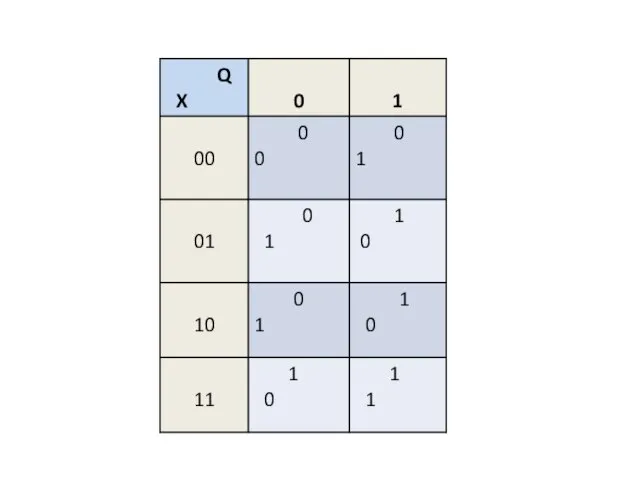
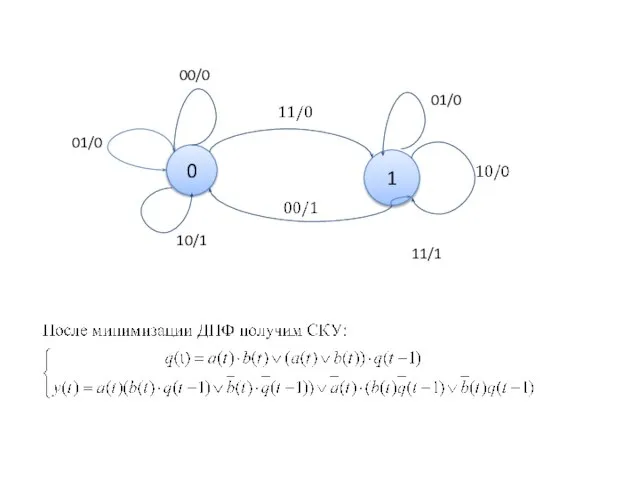
входных сигнала - оценки, полученные сыном в школе: {2, 5}. Начиная с начального состояния s0 (оно помечено входной стрелкой), автомат под воздействием входных сигналов переходит из одного состояния в другое и выдает выходные сигналы - реакции на входы.
Выходы автомата {y0, ..., y5} будем интерпретировать как действия родителя так:
у0: - брать ремень;
у1: - ругать сына;
у2: - успокаивать сына;
у3: - надеяться;
у4: - радоваться;
у5: - ликовать.
Сына, получившего одну и ту же оценку - двойку, ожидает дома совершенно различная реакция в зависимости от предыстории его учебы. Например, после третьей двойки в истории 2,2,2 сына встретят ремнем, а в истории 2,2,5,2 - будут успокаивать. Каждая предыстория определяет текущее состояние автомата. Таким образом, текущее состояние представляет все то, что автомат знает о прошлом с точки зрения его будущего поведения - реакций на последующие входы.










 Математика + естествознание
Математика + естествознание Презентация на тему Прикладные задачи на экстремумы
Презентация на тему Прикладные задачи на экстремумы  Занимательная математика
Занимательная математика Цвет. Знакомство с радугой. 1 класс
Цвет. Знакомство с радугой. 1 класс Тренировка интеллекта. Задачи на логику
Тренировка интеллекта. Задачи на логику Об учебниках по геометрии и теоремах в них. Признаки параллельных и скрещивающихся прямых, параллельности прямой и плоскости
Об учебниках по геометрии и теоремах в них. Признаки параллельных и скрещивающихся прямых, параллельности прямой и плоскости Многогранники. Единица объема. Объем прямоугольного параллелепипеда
Многогранники. Единица объема. Объем прямоугольного параллелепипеда Путешествие по родному краю. Курильский заповедник. Выбери наибольшее число
Путешествие по родному краю. Курильский заповедник. Выбери наибольшее число Презентация на тему Деление обыкновенных дробей (6 класс)
Презентация на тему Деление обыкновенных дробей (6 класс)  Степень и ее свойства
Степень и ее свойства Принак подобия треугольников. Урок 33
Принак подобия треугольников. Урок 33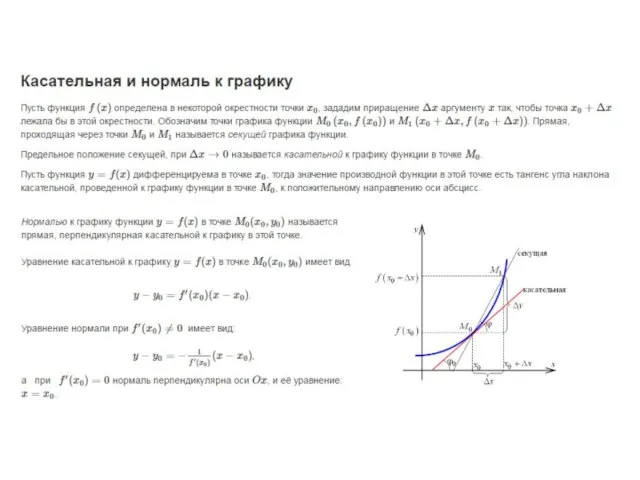 Касательная и нормаль к графику
Касательная и нормаль к графику Задачи на нахождение площади треугольника
Задачи на нахождение площади треугольника Что такое квантор. Будем рассуждать логически
Что такое квантор. Будем рассуждать логически Решение логических задач с помощью нескольких таблиц. Вычислительные таблицы
Решение логических задач с помощью нескольких таблиц. Вычислительные таблицы Игра-тренажер Уроки с Мальвиной. Табличное умножение и деление
Игра-тренажер Уроки с Мальвиной. Табличное умножение и деление Литература
Литература Прямопропорциональные величины
Прямопропорциональные величины Площадь прямоугольника
Площадь прямоугольника Решение текстовых задач с помощью уравнений
Решение текстовых задач с помощью уравнений Презентация на тему Законы арифметических действий (5 класс)
Презентация на тему Законы арифметических действий (5 класс)  Правильные многогранники
Правильные многогранники Математика. Треугольник
Математика. Треугольник Иррациональные неравенства
Иррациональные неравенства Аксонометрические проекции. Самостоятельная работа
Аксонометрические проекции. Самостоятельная работа Многоэтажные дроби. 8 класс
Многоэтажные дроби. 8 класс Системы булевых функций. Лекция 5
Системы булевых функций. Лекция 5 Цилиндр. Конус
Цилиндр. Конус