Математическое моделирование. Линейное программирование

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Линейным программированием называют задачи оптимизации, в которых целевая функция является линейной функцией своих аргументов, а условия, определяющие их допустимые значения, имеют вид линейных уравнений и неравенств [1].
Рассмотрим линейную целевую функцию с одной переменной управления,
причем линейная модель физического процесса выражается как
Подставив второе в первое, получим G-форму целевой функции:
или ,
где
Видно, что при ψ1 > 0 максимум достигается при x = + ∞, а минимум – при x = – ∞.

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Таким образом, линейные целевые функции (как с одной переменной, так и с n-переменными) при отсутствии ограничений не имеют конечного оптимума, поэтому в задачах оптимизации целевой функции ограничения играют принципиальную роль. В дальнейшем будет показано, что совокупность любого числа линейных ограничений выделяет в пространстве x1, x2, …, xn некоторый выпуклый многогранник области возможных значений переменных управления. Экстремум целевой функции достигается в одной из его вершин.
При этом линиями равного уровня целевой функции являются линии, соединяющие точки, в которых значения целевой функции равны между собой.

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Для линейной функции с двумя переменными управления
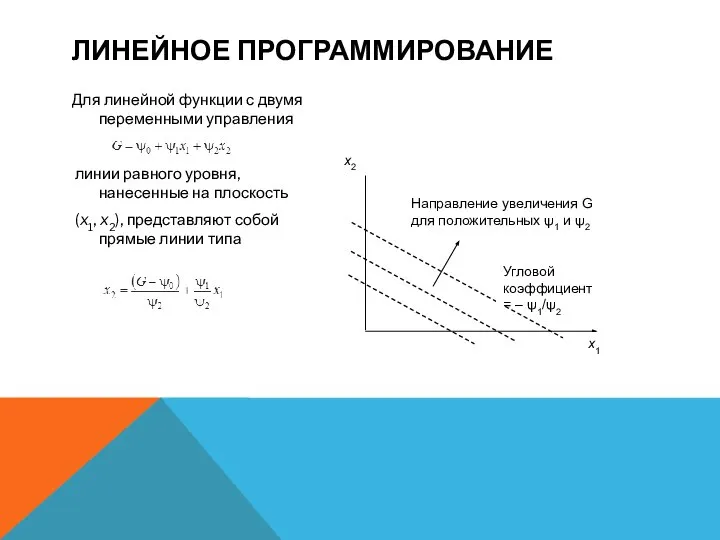
линии равного уровня, нанесенные на плоскость
(x1, x2), представляют собой прямые линии типа

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
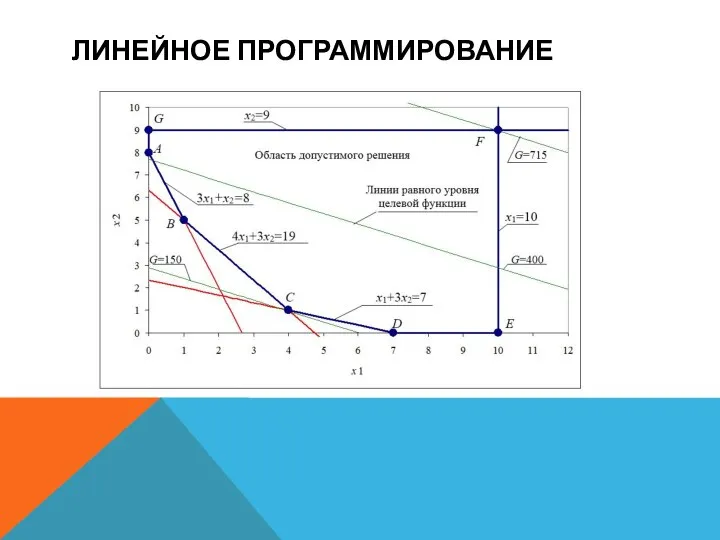
Рассмотрим линейное программирование на примере максимизации функции
при условии, что ограничениями являются
Координаты точек пересечения ограничивающих линий могут быть найдены алгебраическим либо графическим способом. В результате получим
A(0,8); B(1,5); C(4,1); D(7,0); E(10,0); F(10,9); G(0,9).
Минимум находится в точке С, а максимум – в точке F, причем
Gmin = 150, а Gmax = 700.

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

ТРАНСПОРТНАЯ ЗАДАЧА
В городе имеется два склада цемента и два завода ЖБИ, потребляющих этот цемент. Ежедневно с первого склада вывозится 50 т цемента, со второго – 70 т. Этот цемент доставляется на заводы, причем первый завод получает 40 т, второй – 80 т. Допустим, что перевозка одной тонны цемента с первого склада на первый завод стоит 120 руб., с первого склада на второй завод – 160 руб., со второго склада на первый завод – 80 руб., и со второго склада на второй завод – 100 руб. Как нужно спланировать перевозки, чтобы их стоимость была минимальной?
Для того чтобы ответить на этот вопрос, дадим математическую постановку задачи.
Обозначим через x1 и х2 количество цемента, который следует перевезти с первого склада соответственно на первый и второй заводы, а через x3 и x4 – количество цемента, который нужно перевезти со второго склада на первый и второй заводы.

ТРАНСПОРТНАЯ ЗАДАЧА
Эти условия приводят к системе уравнений
xi ≥ 0, i = 1, 2, 3, 4.
Первые два уравнения системы определяют, сколько цемента нужно вывезти с каждого склада, два других уравнения показывают, сколько цемента нужно привезти на каждый завод. Неравенство означает, что в обратном направ­лении с заводов на склады цемент не возят. Общая стоимость всех перевозок определяется формулой
G = 120x1+160x2+80x3+100x4.

ТРАНСПОРТНАЯ ЗАДАЧА
С математической точки зрения задача заключается в том, чтобы найти числа xi, удовлетворяющие заданным условиям и минимизировать стоимость перевозок .
Рассмотрим систему уравнений. Это система четырех уравнении с четырьмя неизвестными. Однако независимыми в ней являются только первые три уравнения, четвертое – их следствие (если сложить 1-е и 2-е уравнения и вычесть 3-е, получится 4-е). Таким образом, фактически нужно рассмотреть следующую систему, эквивалентную:

ТРАНСПОРТНАЯ ЗАДАЧА
В ней число уравнений на единицу меньше числа неизвестных, так что мы можем выбрать какое-нибудь неизвестное, например x1, и выразить через него с помощью уравнений три остальные.
Соответствующие формулы имеют вид
Учитывая неравенства, получаем систему

ТРАНСПОРТНАЯ ЗАДАЧА
из которой 0 ≤ x1 ≤ 40.
Таким образом, задавая любое x1, удовлетворяющее последнему неравенству, и вычисляя x2, x3, x4, мы получим один из возможных планов перевозки. При реализации этого плана с каждого склада будет вывезено и на каждый завод доставлено нужное количество цемента.
Вычислим стоимость перевозок G = 14200–20x1.
Эта формула определяет величину G как функцию одной переменной x1, которую можно выбирать произвольно.
Стоимость окажется минимальной, если мы придадим величине x1 наибольшее возможное значение: x1 = 40. Значения остальных величин xi находятся по x1 .

ТРАНСПОРТНАЯ ЗАДАЧА
Итак, оптимальный по стоимости план перевозок имеет вид
Стоимость перевозок в этом случае составляет 13400 руб. При любом другом допустимом плане перевозок она окажется выше: G > Gmin .

ЗАДАЧА О ИСПОЛЬЗОВАНИИ РЕСУРСОВ
Мебельная фабрика выпускает стулья двух типов. На изготовление одного стула первого типа, стоимостью 800 руб., расходуется 2 п.м досок стандартного сечения, 0,5 м2 обивочной ткани и 2 чел.-ч рабочего времени. Для стульев второго типа аналогичные данные составляют: 1200 руб., 4 п.м, 0,25 м2 и 2,5 чел.-ч.
Допустим, что в распоряжении фабрики имеется 440 п.м досок, 65 м2 обивочной ткани, 320 чел.-ч рабочего времени. Какое количество стульев каждого типа надо изготовить, чтобы в рамках этих ресурсов стоимость произведенной про­дукции была максимальной?
Для ответа на этот вопрос постараемся опять сформулировать задачу как математическую. Обозначим через х1 и х2 запланированное к производству число стульев соответственно первого и второго типов.

ЗАДАЧА О ИСПОЛЬЗОВАНИИ РЕСУРСОВ
Ограниченный запас сырья и трудовых ресурсов означает, что x1 и х2 должны удовлетворять неравенствам
Кроме того, по смыслу задачи они должны быть неотрицательными

ЗАДАЧА О ИСПОЛЬЗОВАНИИ РЕСУРСОВ
Стоимость запланированной к производству продукции определяется формулой
G(x1,x2) = 800x1+1200x2.
Итак, с математической точки зрения задача составления оптимального по стоимости выпущенной продукции плана фабрики сводится к определению пары целых чисел x1, x2, удовлетворяющих линейным неравенствам, и дающих наибольшее значение линейной функции. Мы опять получили типичную задачу линейного программирования. По своей постановке она несколько отличается от транспортной задачи, однако это различие не существенно.

ЗАДАЧА О ИСПОЛЬЗОВАНИИ РЕСУРСОВ
Для анализа сформулированной задачи рассмотрим плоскость и введем на ней декартову систему координат x1, x2. Найдем на этой плоскости множество точек, координаты которых удовлетворяют заданным условиям. При этом множество лежит в первой четверти. Выясним смысл ограничений, которые задаются неравенствами. Проведем на плоскости прямую, определяемую уравнением 2x1+4x2 = 440.
Она делит плоскость на две полуплоскости. На одной из них, расположенной ниже прямой, функция f1(x1,x2) = 2x1+4x2–440 принимает отрицательные значения; на другой, расположенной выше прямой, – положительные. Таким образом, первое из неравенств выполняется на множестве точек, которое включает в себя прямую и полуплоскость, расположенную ниже этой прямой. На рисунке соответствующая часть плоскости заштрихована.

ЗАДАЧА О ИСПОЛЬЗОВАНИИ РЕСУРСОВ

ЗАДАЧА О ИСПОЛЬЗОВАНИИ РЕСУРСОВ
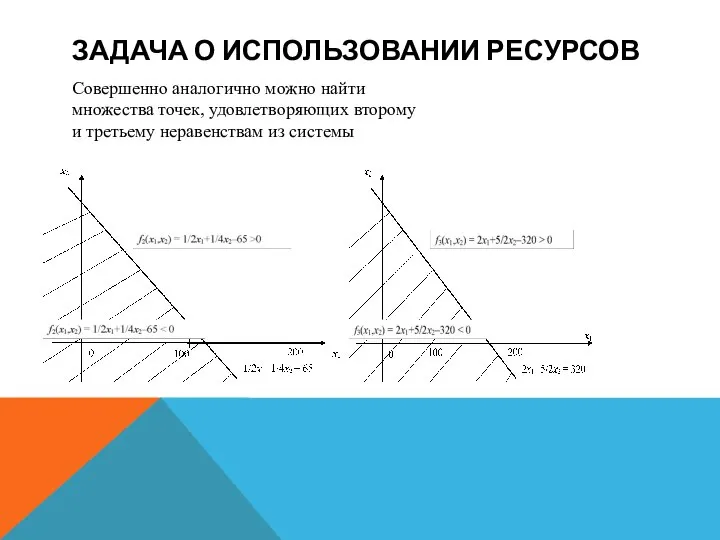
Совершенно аналогично можно найти множества точек, удовлетворяющих второму и третьему неравенствам из системы

ЗАДАЧА О ИСПОЛЬЗОВАНИИ РЕСУРСОВ
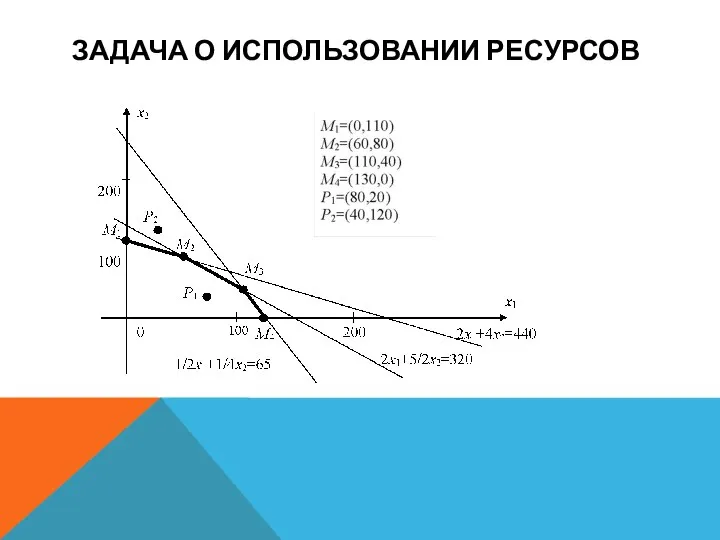
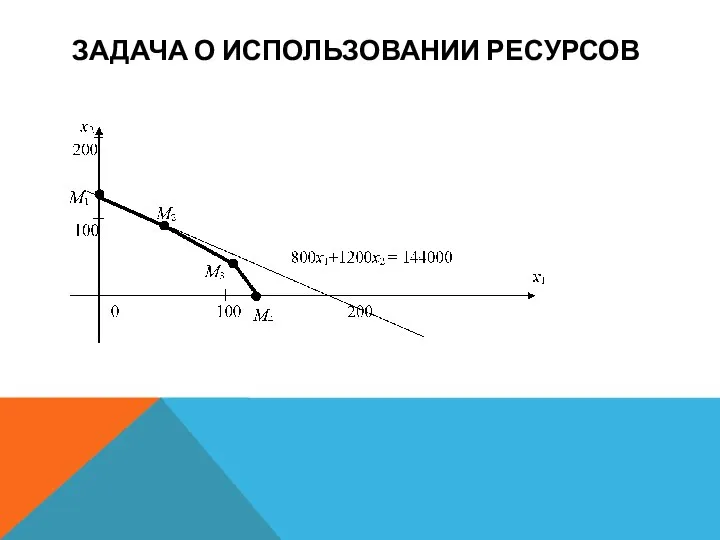
Возьмем пересечение трех найденных множеств и выделим его часть, расположенную в первой четверти. В результате получим множество точек, удовлетворяющих всей совокупности ограничений. Данное множество имеет вид пятиугольника, показанного на рис. Его вершинами являются точки пересечения прямых, на которых неравенства переходят в точные равенства. Координаты вершин пятиугольника указаны на рисунке.

ЗАДАЧА О ИСПОЛЬЗОВАНИИ РЕСУРСОВ

ЗАДАЧА О ИСПОЛЬЗОВАНИИ РЕСУРСОВ
Любой точке Р с целочисленными координатами (x1, x2), принадлежащей данному пятиугольнику, соответствует план выпуска стульев, который может быть выполнен при имеющихся запасах сырья и трудовых ресурсах (реализуемый план). Наоборот, если точка Р не принадлежит пятиугольнику, то соответствующий план не может быть выполнен (нереализуемый план).
Рассмотрим на плоскости x1, x2 линии уровня целевой функции: 800x1+1200x2 = C.
Это уравнение описывает семейство прямых, параллельных прямой
800x1+1200x2 = 0.
При параллельном переносе этой прямой вправо параметр С возрастает, влево – убывает.
Свойства функции тесно связаны с прямыми. Вдоль каждой из них она сохраняет постоянное значение, равное С, а при переходе с одной прямой на другую ее значение меняется.

ЗАДАЧА О ИСПОЛЬЗОВАНИИ РЕСУРСОВ
Будем рассматривать только первую четверть. Предположим, что мы перешли из точки Р1, расположенной на одной прямой, в точку Р2, расположенную на другой прямой (рис). Если вторая прямая расположена дальше от начала координат, чем первая, то функция G при этом переходе возрастет. Отсюда следует важный вывод: оптимальный план должен располагаться на прямой семейства, наиболее удаленной от начала координат.

ЗАДАЧА О ИСПОЛЬЗОВАНИИ РЕСУРСОВ

ЗАДАЧА О ИСПОЛЬЗОВАНИИ РЕСУРСОВ
Этот вывод позволяет закончить решение задачи. Рассмотрим рис. На нем воспроизведен пятиугольник реализуемых планов и нарисована прямая семейства, проходящая через точку М2 с координатами (60, 80). Она является предельной прямой семейства, имеющей общую точку с пятиугольником. Если мы попытаемся с помощью параллельного переноса отодвинуть ее дальше от начала координат, то получим прямую, не имеющую общих точек с пятиугольником, т. е. соответствующие планы нереализуемы.

ЗАДАЧА О ИСПОЛЬЗОВАНИИ РЕСУРСОВ

ЗАДАЧА О ИСПОЛЬЗОВАНИИ РЕСУРСОВ
Итак, оптимальный план найден, – он предписывает производство 60 стульев первого типа и 80 стульев второго типа. Стоимость этой продукции 144000 руб. На выполнение плана нужно затратить: 440 п.м досок, 50 м2 обивочной ткани, 320 чел. -ч рабочего времени.
Видно, что оптимальный план требует полного использования запаса досок и трудовых ресурсов, в то время как обивочная ткань будет израсходована не полностью – останется 15 м2.
Этот результат ясен из последнего рис. Точка M2, определяющая оптимальный план, является вершиной пятиугольника.
Она лежит на пересечении прямых 2x1+4x2 = 440 и 2x1+5/2x2 = 320.

ЗАДАЧА О ИСПОЛЬЗОВАНИИ РЕСУРСОВ
Уравнения этих прямых получаются из первого и третьего условий системы при замене их на строгие равенства. Это означает полный расход досок и трудовых ресурсов. Однако точка М2 не принадлежит прямой
1/2x1+1/4x2 = 65,
так что второе условие связано с ограниченным запасом обивочной ткани, имеет форму неравенства 50 < 65.
Проведенный анализ показывает, что дальнейшее увеличение стоимости продукции регламентируется запасом досок и трудовыми ресурсами.