Содержание
- 2. Предмет математика настільки серйозний, що корисно не упускати випадків робити його цікавим. Б.Паскаль
- 3. 2 Зміст Паралелограм. Паралелограм і його властивості. Прямокутник і його властивості. Площа і периметр прямокутника. Задачі.
- 4. Мета: систематизувати і повторити знання про властивості паралелограмів; закріпити уміння і навички використання властивостей при розв’язуванні
- 5. Це ми повинні знати. 1. Яка фігура називається паралелограмом? 2. Яка фігура називається прямокутником; ромбом; квадратом?
- 6. Що ми повинні вміти? 1. Систематизувати і узагальнювати знання про види, властивості, ознаки паралелограмів. 2. Вдосконалювати
- 7. Паралелограм і його властивості А В С D Паралелограм АВСD - це чотирикутник, у якого протилежні
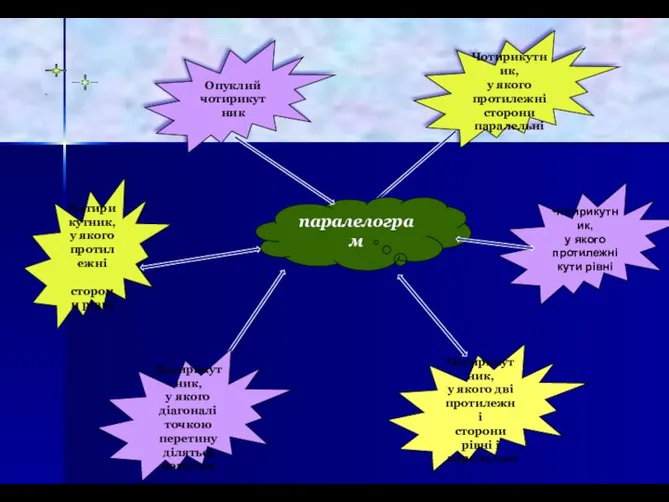
- 8. паралелограм Чотирикутник, у якого протилежні кути рівні Чотирикутник, у якого протилежні сторони паралельні Чотирикутник, у якого
- 9. а) Якщо дві протилежні сторони чотирикутника паралельні й рівні, то цей чотирикутник — паралелограм, б) Якщо
- 10. Закінчіть речення так, щоб утворилося істинне твердження. Паралелограм — це чотирикутник, у якого протилежні сторони... У
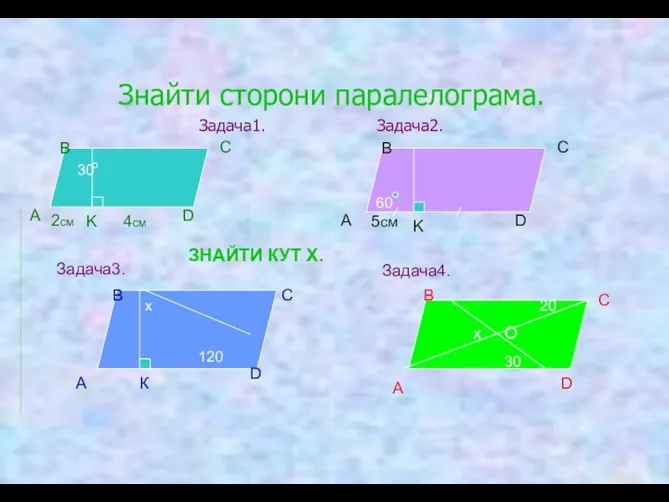
- 11. Знайти сторони паралелограма. Задача1. Задача2. 30 А В С D K 60 А В С D
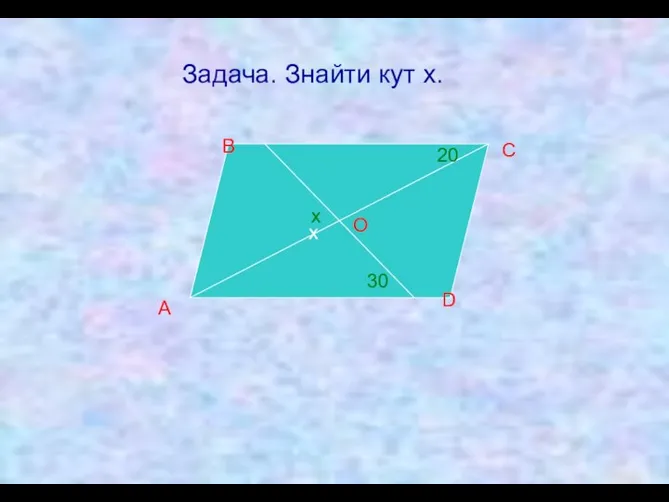
- 12. Задача. Знайти кут х. А В С D х х О 20 30
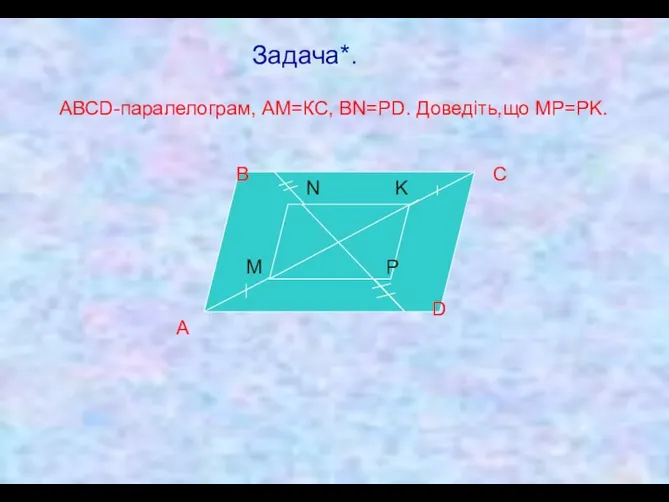
- 13. Задача*. АВСD-паралелограм, АМ=КС, ВN=PD. Доведіть,що MP=PK. А В С D M N K P
- 14. Прямокутник А В С D Означення. Прямокутник - це чотирикутник, у якого всі кути прямі, тобто,
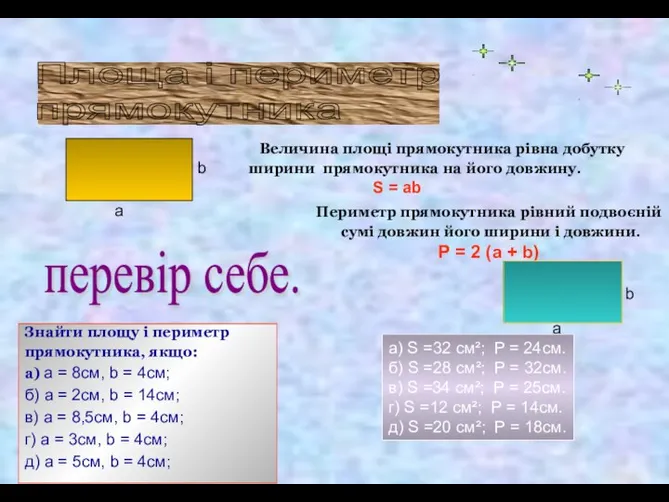
- 15. Периметр прямокутника рівний подвоєній сумі довжин його ширини і довжини. Р = 2 (a + b)
- 16. Працюємо разом А В С D Задача 1. Бісектриса одного з кутів прямокутника ділить його сторону
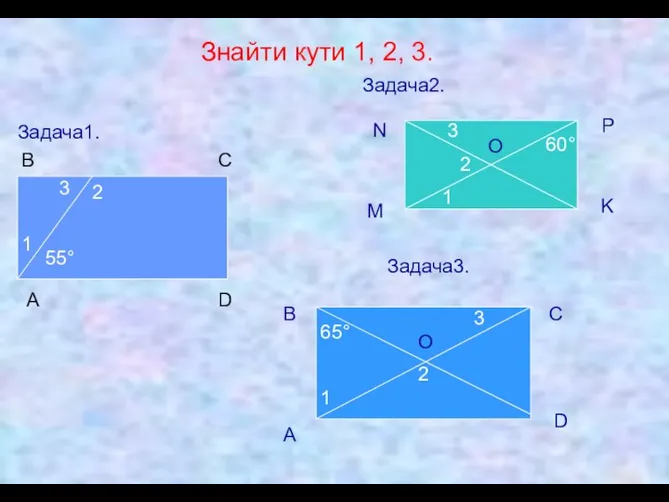
- 17. Знайти кути 1, 2, 3. Задача1. А B С D 55° 1 2 3 Задача2. 60°
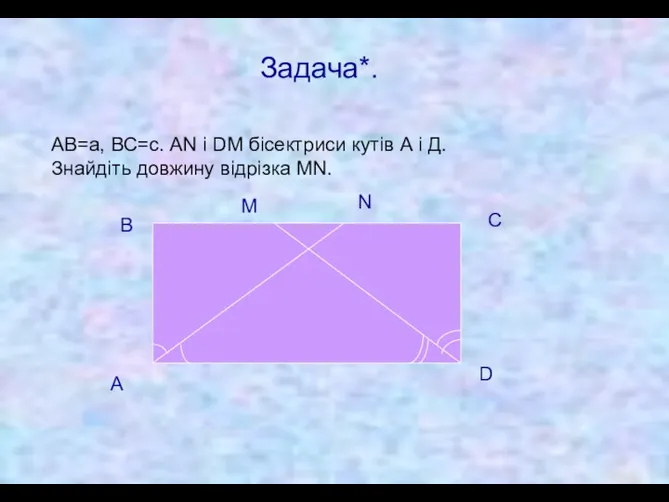
- 18. Задача*. АВ=а, ВС=с. AN і DM бісектриси кутів А і Д. Знайдіть довжину відрізка MN. А
- 19. Означення. Ромб - це чотирикутник, у якого всі сторони рівні. Слово «ромб» вперше уживається у працях
- 20. Площа ромба Площа ромба рівна половині добутку його діагоналей. S = ½d1 d2 2. Оскільки ромб
- 21. Працюємо разом Знайти периметр і площу ромба. а) a = 8см; б) a = 2см; в)
- 22. Перевір себе: Теорема 1. Діагоналі прямокутника рівні. Твердження теореми випливає з рівності прямокутних трикутників ВАD і
- 23. А В С D Працюємо разом. Нехай АВСD - даний ромб, а О – точка перетину
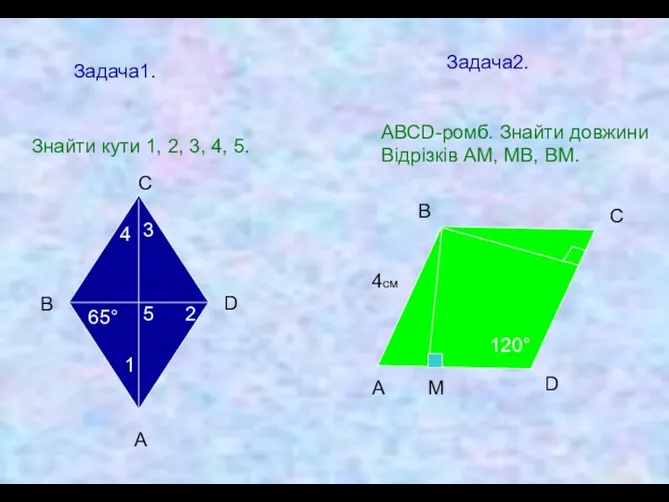
- 24. Задача1. Знайти кути 1, 2, 3, 4, 5. 65° 1 2 5 3 4 А В
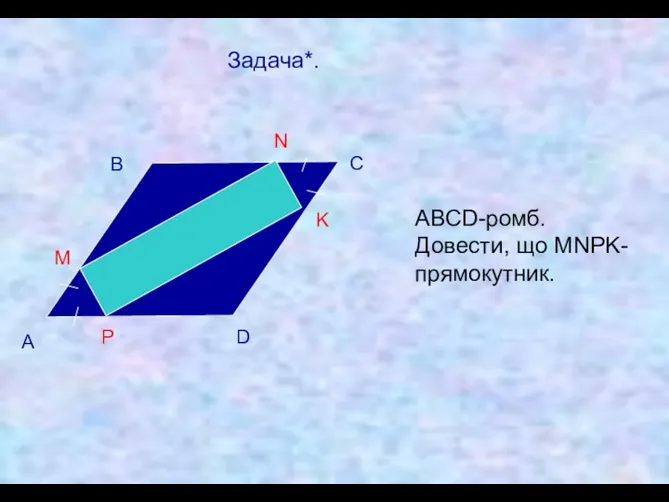
- 25. Задача*. А В С D M N K P АВСD-ромб. Довести, що MNPK- прямокутник.
- 26. Квадрат – це прямокутник у якого всі сторони рівні. Квадрат є також ромбом у якого всі
- 27. Квадрат володіє найбільшою кількістю симетрій серед всіх чотирикутників. При розрізанні квадрата діагоналлю отримуємо два рівнобедрених прямокутних
- 28. Нехай a - сторона квадрата, R - радіус описаного кола, r - радіус вписаного кола. Тоді
- 29. АЛГОРИТМ ПОБУДОВИ ВПИСАНОГО КВАДРАТА Побудуйте довільне коло. Проведіть перпендикулярні діаметри цього кола. Через точки перетину кола
- 30. Працюємо в групах. І група. Дати відповідь: Чи буде чотирикутник квадратом, якщо його діагоналі: а) рівні
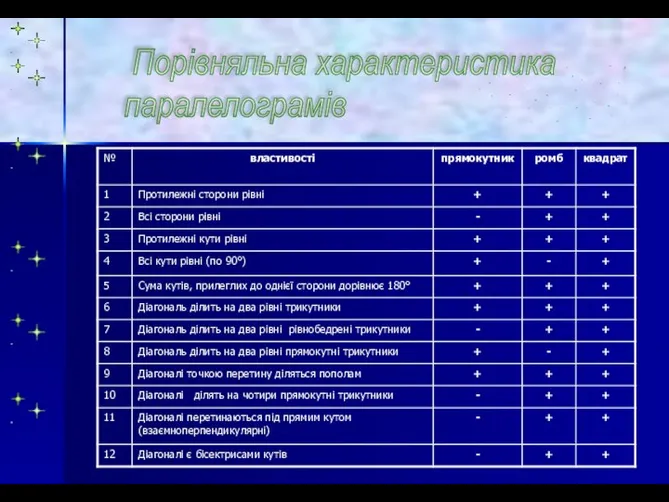
- 31. Порівняльна характеристика паралелограмів
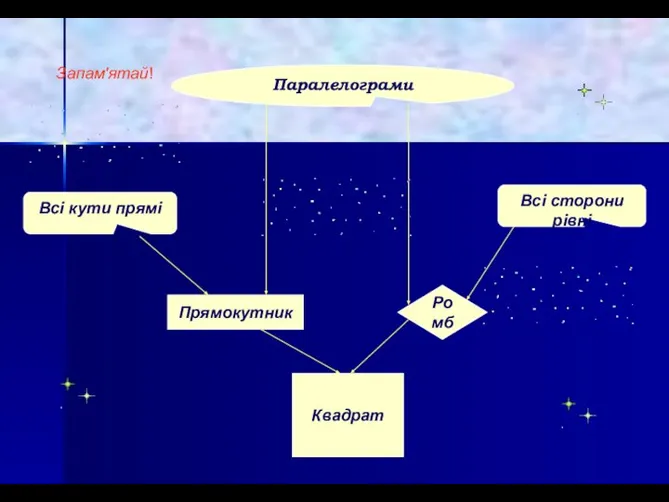
- 32. Паралелограми Всі кути прямі Всі сторони рівні Квадрат Прямокутник Ромб Запам'ятай!
- 33. прямокутники ромби квадрати поралелограми паралелограми
- 34. Додаткові задачі Вчимося використовувати прийом нанизування на одну ідею декілька задач 1 2 3 4 5
- 35. А Працюємо разом В Р С D 1 2 Розв'язуємо задачі з коментарем. Задача 1. ∟1
- 36. А Прямокутник В С D О Працюємо в групах І група. Задача 1. Різниця периметрів ∆АВD
- 37. Прямокутник Працюємо разом А В D М С 1 2 3 Задача 1. Дано: АВ =
- 38. Працюємо разом Ромб А В С D О 1 Задача 1. Периметр ромба АВСD дорівнює 40
- 40. Скачать презентацию


























 Финансовая грамотность
Финансовая грамотность Комплексные числа. Все формы
Комплексные числа. Все формы Роль диагностики в обучении математи
Роль диагностики в обучении математи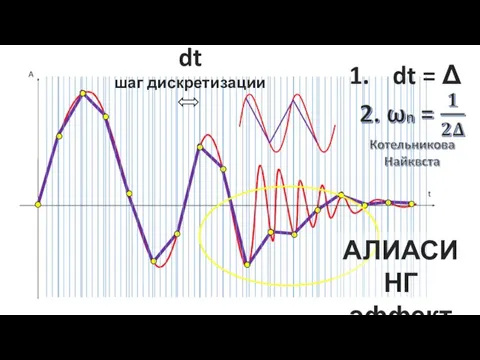 Алиасинг эффект. АЦП σ-δ. Интегратор
Алиасинг эффект. АЦП σ-δ. Интегратор Многогранники
Многогранники Введение в стереометрию
Введение в стереометрию Числа и точки на прямой
Числа и точки на прямой Математика, Устный счёт
Математика, Устный счёт Математический калейдоскоп Областная интеллектуальная игра
Математический калейдоскоп Областная интеллектуальная игра Цикломатика графов
Цикломатика графов Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Понятие объёма
Понятие объёма Производная сложной функции
Производная сложной функции Транспортная задача. Методы нахождения начального решения транспортной задачи
Транспортная задача. Методы нахождения начального решения транспортной задачи Построение сечений
Построение сечений Иррациональные неравенства
Иррациональные неравенства Правильная треугольная пирамида. Задачи
Правильная треугольная пирамида. Задачи Графики линейных функций
Графики линейных функций Решение трансцендентных уравнений
Решение трансцендентных уравнений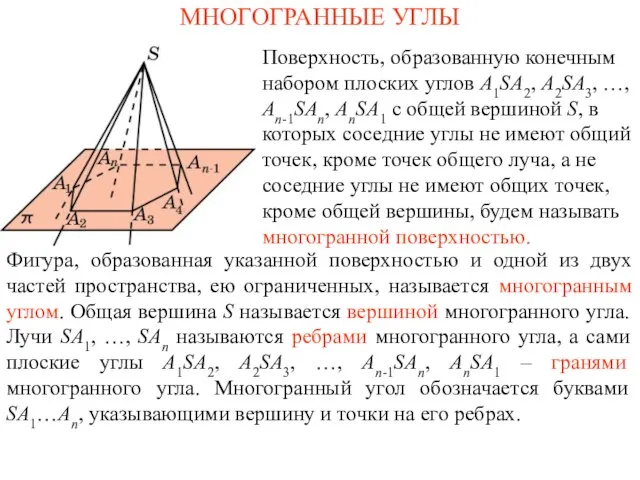 Презентация на тему Многогранные углы
Презентация на тему Многогранные углы  Проценты. Задачи
Проценты. Задачи Прохождение случайной волны через отверстие в экране. Теорема Ван-Циттерта-Цернике
Прохождение случайной волны через отверстие в экране. Теорема Ван-Циттерта-Цернике Методология нелинейного функционально - факторного моделирования природных и техногенных явлений
Методология нелинейного функционально - факторного моделирования природных и техногенных явлений Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников Десятичные дроби
Десятичные дроби Степенная функция
Степенная функция Число 0. Цифра 0. Урок №31
Число 0. Цифра 0. Урок №31 Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями