Слайд 2Определитель квадратной матрицы.
Определение
Каждой квадратной матрице А порядка n (где n≥1) ставится

в соответствие число, называемое определителем матрицы А, обозначаемое ⎜А ⎜, вычисляемое по правилу:
и так далее:
Слайд 3Определитель квадратной матрицы.
Определение

Слайд 4Определитель квадратной матрицы
Определитель n -го порядка:
Эта формула называется разложением определителя

n -го порядка по первой строке.
Слайд 5Определитель квадратной матрицы
Пример 1. Вычисление определителя путем разложения по элементам 1-ой

строки.
Слайд 6Определитель квадратной матрицы
Теорема. Определитель может быть вычислен разложением по элементам его

л ю б о й строки или столбца.
Разложение определителя
по i-той строке:
Разложение определителя
по j-му столбцу:
Слайд 7Определитель квадратной матрицы
Пример 1 (продолжение)
Вычисление определителя путем разложения по элементам 3-й

строки
Вычисление определителя путем разложения по элементам 4-го столбца
Слайд 8Свойства определителей
1. Определитель не меняется при замене в нем всех строк соответствующими

(по номеру) столбцами, т.е. .
2. Определитель равен нулю, если содержит нулевую строку или нулевой столбец.
3. Определитель равен нулю, если содержит две одинаковые строки или два одинаковых столбца.
Слайд 9Свойства определителей
4. Определитель треугольной матрицы равен произведению элементов главной диагонали матрицы

Слайд 10Свойства определителей
5. Определитель изменит знак на противоположный, если в нем поменять местами

любые две строки или два столбца (то есть применено элементарное преобразование первого типа).
6. Если строку (столбец) определителя умножить на некоторое число (то есть применено элементарное преобразование третьего типа), то определитель умножится на это число.
Слайд 11Свойства определителей
7. Определитель не изменится, если в нем заменить строку суммой этой

строки и некоторой другой, вспомогательной, предварительно умноженной на какое-либо число (то есть применено элементарное преобразование второго типа).
8. Определитель произведения квадратных матриц равен произведению определителей сомножителей. т.е.
Слайд 12Применение свойств определителя для вычисления определителей
Пример 1. Вычислить определитель пятого порядка:
Решение.

Слайд 13Применение свойств определителя для вычисления определителей

Слайд 14Применение свойств определителя для вычисления определителей

Слайд 15Применение свойств определителя для вычисления определителей
Пример 2. Вычислить определитель пятого порядка путем

приведения к верхнетреугольному виду:
Решение.
Слайд 16Применение свойств определителя для вычисления определителей
Решение.

Слайд 17Свойства определителей
Определение. Алгебраическим дополнением элемента матрицы порядка n называется число, равное
Используя

алгебраическое дополнение, метод вычисления определителя матрицы примет вид:
Слайд 19Обратная матрица
Определение. Матрица называется невырожденной, если определитель этой матрицы отличен от нуля:

в противном случае матрица называется вырожденной.
Теорема. Если матрица A имеет обратную, то эта матрица является невырожденной:
Слайд 20Методы вычисления обратной матрицы
Теорема. Всякая невырожденная матрица имеет обратную, причем
где алгебраическое дополнения

элемента матрицы A.
Слайд 21Пример вычисления обратной матрицы
Пример. Найти матрицу, обратную данной:
Решение.

Слайд 22Пример вычисления обратной матрицы
Найдем алгебраические дополнения:
Тогда

Слайд 23Методы вычисления обратной матрицы
Обратная матрица для матрицы 2-го порядка
Пусть
Пример.

Слайд 24Методы вычисления обратной матрицы
Метод Жордана-Гаусса вычисления обратной матрицы (метод присоединенной матрицы)
Дана матрица

A. Составим расширенную матрицу , приписав после матрицы A за вертикальной чертой единичную матрицу той же размерности.
Если с помощью элементарных преобразований удастся преобразовать полученную расширенную матрицу к виду, в котором слева будет находиться единичная матрица, то справа будет находиться обратная матрица A-1, т.е.
Слайд 25Пример вычисления обратной матрицы

Слайд 26Пример вычисления обратной матрицы
Следовательно, заключаем


























 Угол между векторами. Скалярное произведение векторов
Угол между векторами. Скалярное произведение векторов ВЛИЯНИЕ КОЭФФИЦИЕНТОВ а, b и с НА РАСПОЛОЖЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ
ВЛИЯНИЕ КОЭФФИЦИЕНТОВ а, b и с НА РАСПОЛОЖЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ Использование Microsoft Exel в проектных работах по математике
Использование Microsoft Exel в проектных работах по математике Задания со спичками
Задания со спичками Формирование алгоритмического мышления у младших школьников
Формирование алгоритмического мышления у младших школьников Занимательная геометрия. Треугольник - три угла
Занимательная геометрия. Треугольник - три угла Загадки и тайны треугольника
Загадки и тайны треугольника Составление переводной работы по алгебре в формате ЕГЭ, 2017-2018 учебный год
Составление переводной работы по алгебре в формате ЕГЭ, 2017-2018 учебный год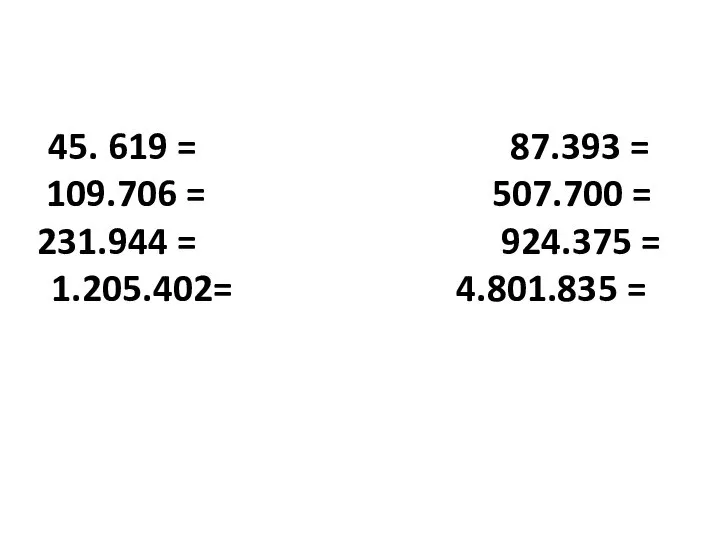 Разряды чисел
Разряды чисел Логика
Логика Решение задания 12 ЕГЭ (профиль)
Решение задания 12 ЕГЭ (профиль) Презентация на тему Признаки равенства и подобия треугольников
Презентация на тему Признаки равенства и подобия треугольников  Уравнения и неравенства с двумя переменными, содержащие параметр
Уравнения и неравенства с двумя переменными, содержащие параметр Справочный материал. 9 класс
Справочный материал. 9 класс Вычитание дроби из целого числа (урок 116)
Вычитание дроби из целого числа (урок 116) Обобщение по 3-м формулам сокращенного умножения
Обобщение по 3-м формулам сокращенного умножения Четырёхугольники, их признаки и свойства. Геометрия. 8 класс
Четырёхугольники, их признаки и свойства. Геометрия. 8 класс Назначение формулы
Назначение формулы Графики функции
Графики функции Интересная математика
Интересная математика Применение интеграла к вычислению площадей
Применение интеграла к вычислению площадей Решение задач с пропорциональными величинами
Решение задач с пропорциональными величинами Какие бывают числа
Какие бывают числа Презентация на тему Формулы сокращенного умножения. Представление выражения в виде многочлена
Презентация на тему Формулы сокращенного умножения. Представление выражения в виде многочлена  Деление суммы на число
Деление суммы на число История введения понятия функции в школьный курс математики и современность
История введения понятия функции в школьный курс математики и современность Учимся писать цифру 8
Учимся писать цифру 8 Проект по математике Задачи-расчеты из моей жизни
Проект по математике Задачи-расчеты из моей жизни