Основное свойство первообразной

ЗАДАНИЕ
1. Повторить, слайд №3,4,6,7
2.Слайд №8,9 рассмотреть примеры нахождения первообразных
3.Решить самостоятельно, слайд №10

Теорема:
Любая первообразная для функции
f на промежутке может быть
записана в виде
F(х)+С, где
F(х) одна из первообразных для f(х)
С – произвольная постоянная

Доказательство:
По определению первообразной
F'(х) = f(х), проверим
(F(х)+С)‘ = f(х) + 0
Ч.т.д

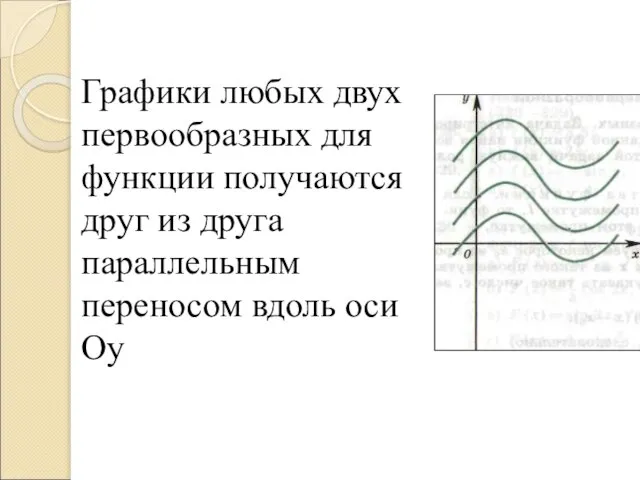
Графики любых двух первообразных для функции получаются друг из друга параллельным переносом вдоль оси Оу

Запомни!
Первообразная для f(х) обозначается F(х)

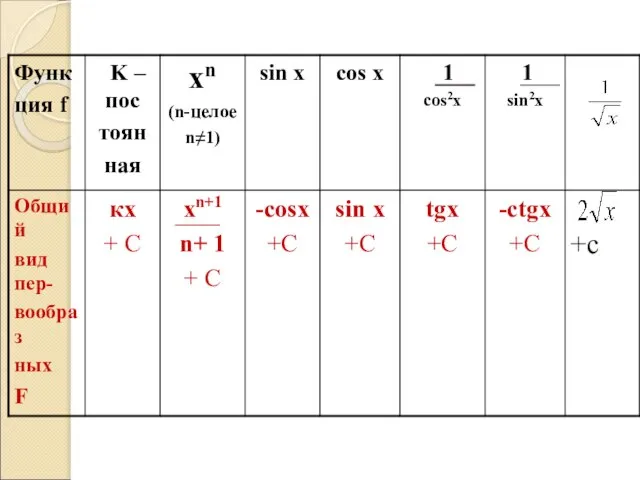
Найдите первообразные
Пример №1. f(х) = 4
Смотрим в верхнюю строку таблицы, первый столбик. Там написано к –постоянная. Опускаемся во вторую строку, там написано кх. Вместо к ставим наше число 4, будет F(х) = 4х + С
Аналогично, для f(х) =-5, F(х) = -5х + С

Пример №2. f(х) = х2
Смотрим в верхнюю строку таблицы, второй столбик. Там написано хn ,у нас
n = 2. Опускаемся во вторую строку, там написано хn/n+1. Вместо n ставим наше число , будет F(х) = х2+1/2 +1+С=х3/3 +С
Аналогично для f(х) =х3, F(х) = х4/4 + С

Найдите первообразные
1.f(х) =10
2.f(х) = -3
3.f(х) =х-5;
4. f(х) =х-6;
5.f(х) =х-8;
7. f(х) = 12
7.f(х) = 7
8. f(х) = х9;
9. f(х) =х4

Найдите первообразные
16.f(х) =х7 - 10;
17. f(х) =х3 + sin x+ 2;
18.f(х) =х8;
19. f(х) = sin x + 5;
20.f(х) = cos x;
21. f(х) = х2+1;
22. f(х) =х9 + 30.

23.f(х) =4;
24. f(х) =-5;
25.f(х) =10;
26. f(х) =9;
27.f(х) =х2;
28.f(х) =х3;
29.f(х) =х5;
30.f(х) =х9;
31.f(х) =х-5;
32. f(х) =х10;
33.f(х) =х-8;
34.f(х) = sin x;
35.f(х) = cos x;