Содержание
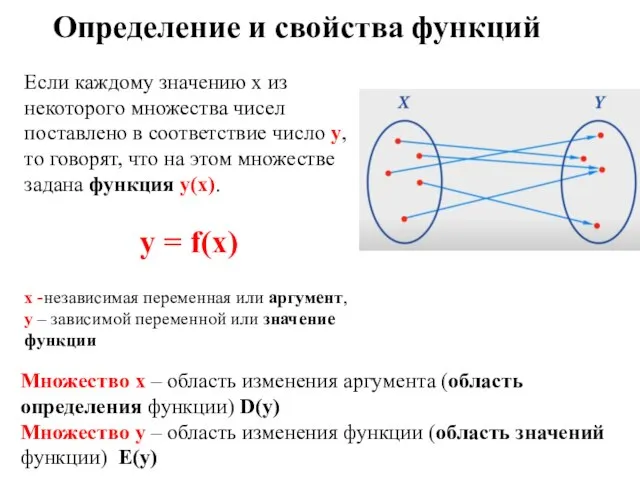
- 2. Определение и свойства функций Если каждому значению х из некоторого множества чисел поставлено в соответствие число
- 5. Функцию y = f(x) называют возрастающей на множестве Х, если для любых двух элементов из этого
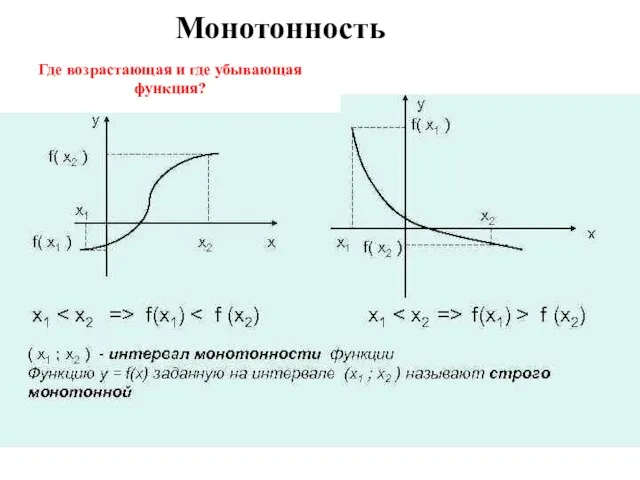
- 6. Монотонность Где возрастающая и где убывающая функция?
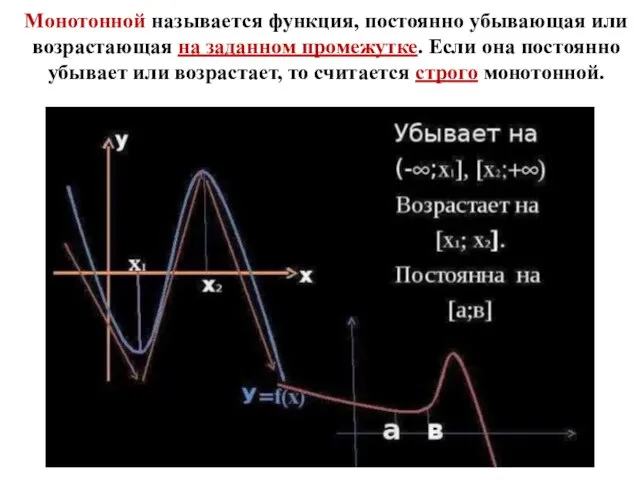
- 7. Монотонной называется функция, постоянно убывающая или возрастающая на заданном промежутке. Если она постоянно убывает или возрастает,
- 8. Четность функции Пример
- 9. Периодичность
- 10. Непрерывность
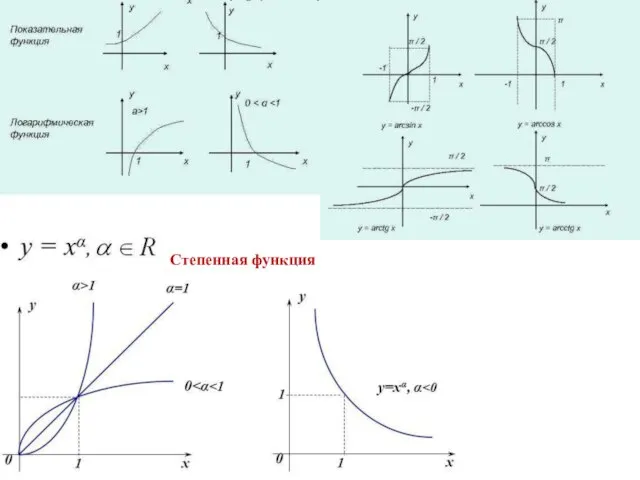
- 12. Степенная функция
- 13. Степенная функция
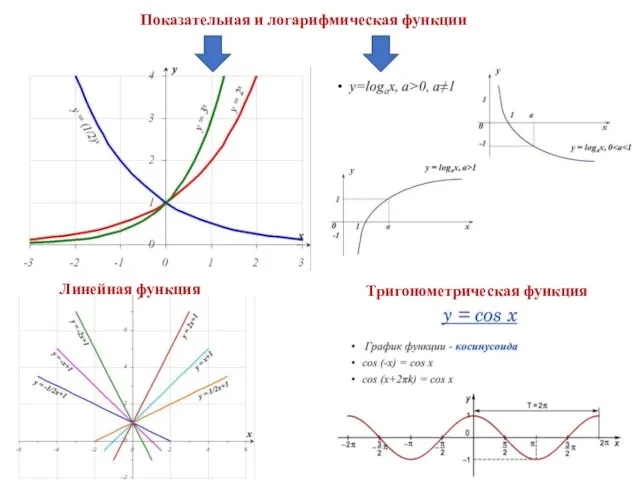
- 14. Показательная и логарифмическая функции Линейная функция Тригонометрическая функция
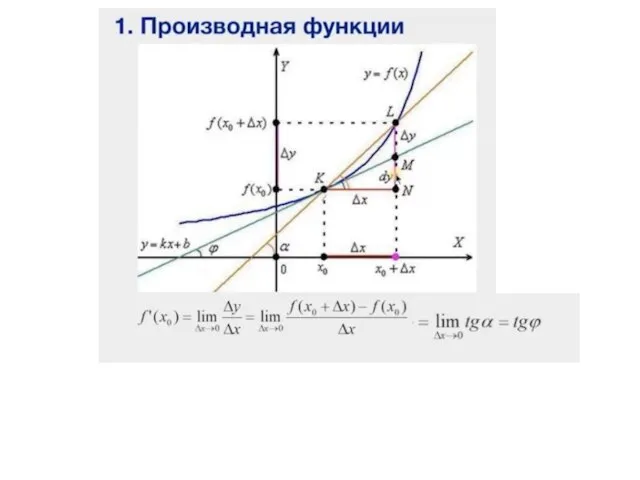
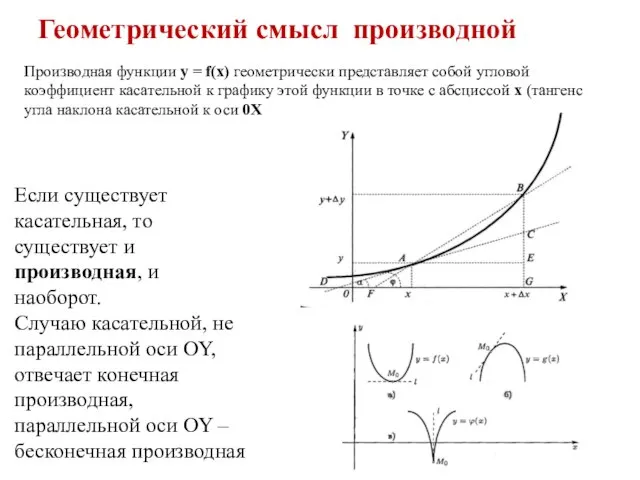
- 16. Производная функции у = f(x) геометрически представляет собой угловой коэффициент касательной к графику этой функции в
- 17. Физический смысл - производная функции отражает скорость изменения функции при изменении ее аргумента. Например, если x
- 18. Физический смысл производной
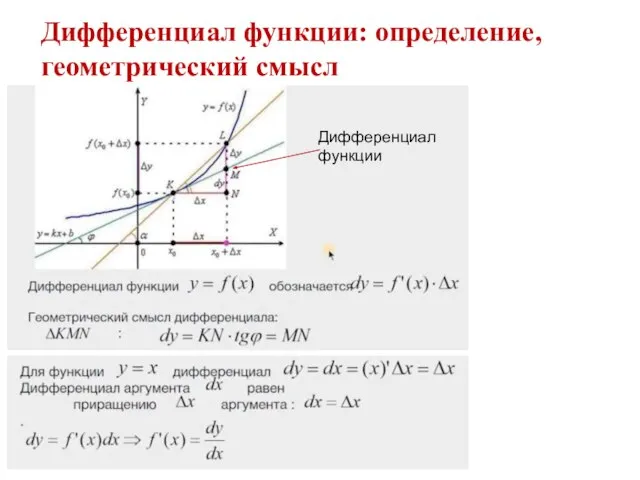
- 19. Дифференциал функции Дифференциал функции: определение, геометрический смысл
- 20. Дифференциал функции: определение, геометрический смысл Дифференциалом функции называется произведение производной этой функции на приращение ее аргумента
- 21. Производные элементарных функций
- 22. Производные и дифференцирование
- 23. Вычисления производных
- 24. Вычисления производных
- 25. y = (2x+3) sin x
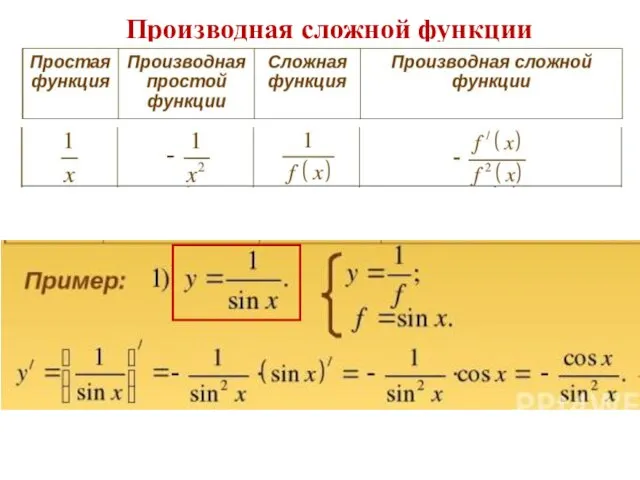
- 28. Производная сложной функции
- 29. Производная сложной функции
- 30. Производная сложной функции
- 31. Производная сложной функции
- 32. Найти область определения функции Найти точки разрыва функции и ее односторонние пределы в этих точках Выяснить,
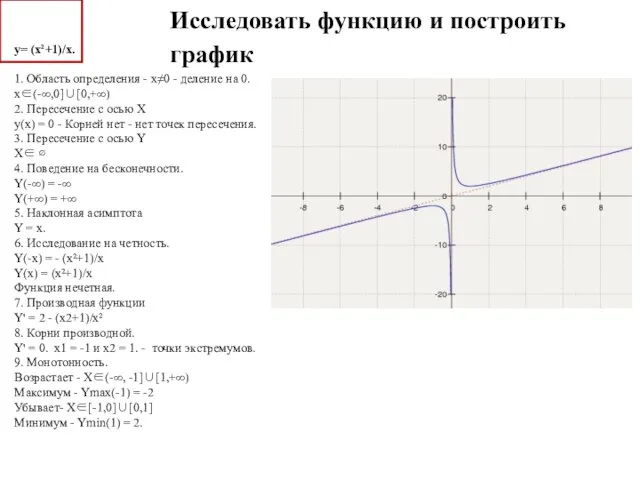
- 33. Исследовать функцию и построить график y= (x²+1)/x. 1. Область определения - x≠0 - деление на 0.
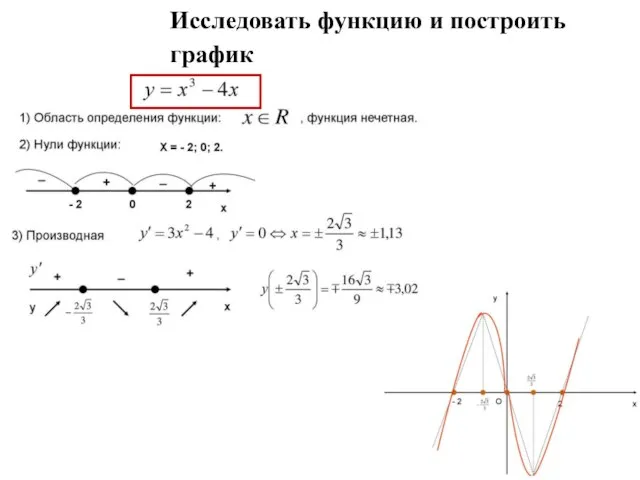
- 34. Исследовать функцию и построить график
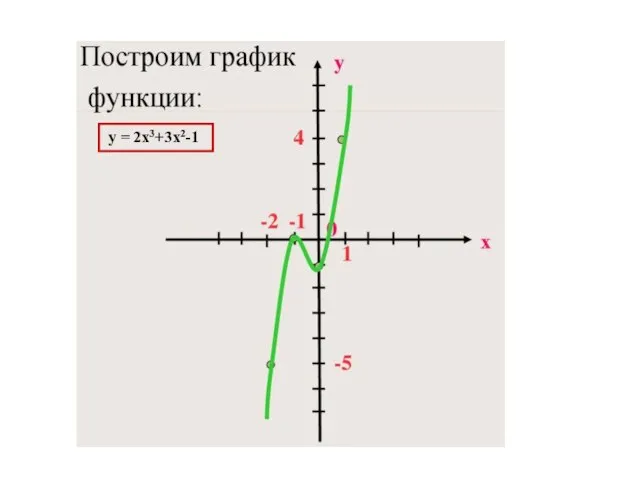
- 37. y = 2x3+3x2-1
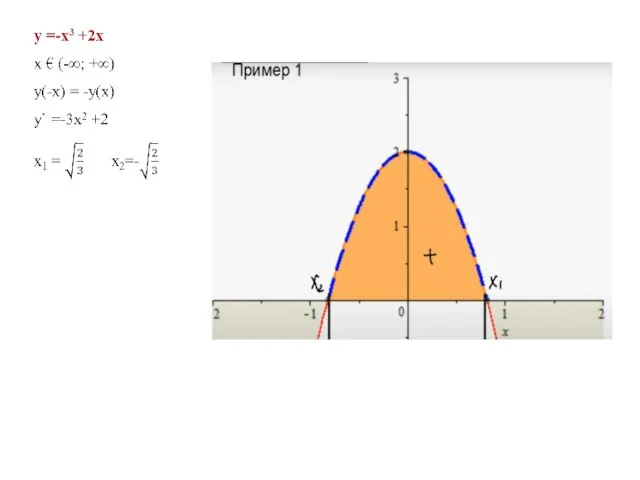
- 39. Пример
- 40. Обратные примеры: По графику функции, изображенному на рисунке, указать:
- 42. «Неберущиеся» интегалы Интеграл, который не выражается через элементарные функции, т.е. его нельзя найти
- 43. Неопределенный интеграл. Свойства
- 44. Неопределенный интеграл элементарных функций
- 45. Неопределенный интеграл. Метод замены переменных
- 46. Неопределенный интеграл. Метод замены переменных
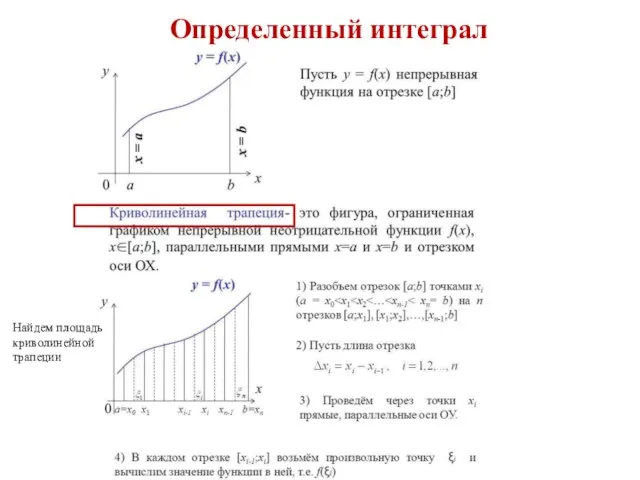
- 47. Определенный интеграл Найдем площадь криволинейной трапеции
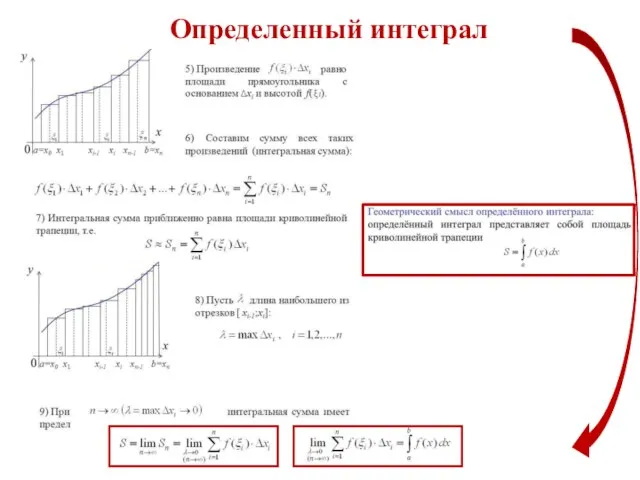
- 48. Определенный интеграл
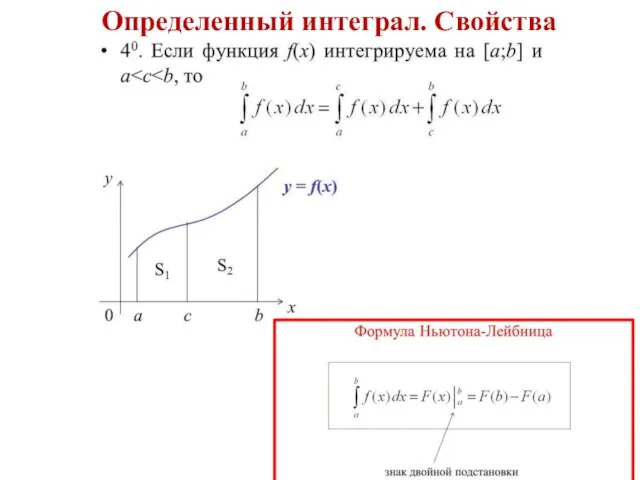
- 49. Определенный интеграл. Свойства
- 50. Определенный интеграл. Свойства
- 51. Определенный интеграл. Свойства
- 52. Определенный интеграл. Свойства
- 53. Примеры. Прямое интегрирование
- 54. Примеры. Метод подстановки
- 55. Примеры. Метод подстановки
- 56. Примеры. Метод подстановки
- 57. Интегрирование по частям
- 58. Интегрирование суммы трех функций
- 59. Интегрирование в физике
- 60. Аппроксимация медицинских (антропометрических) данных функциями.
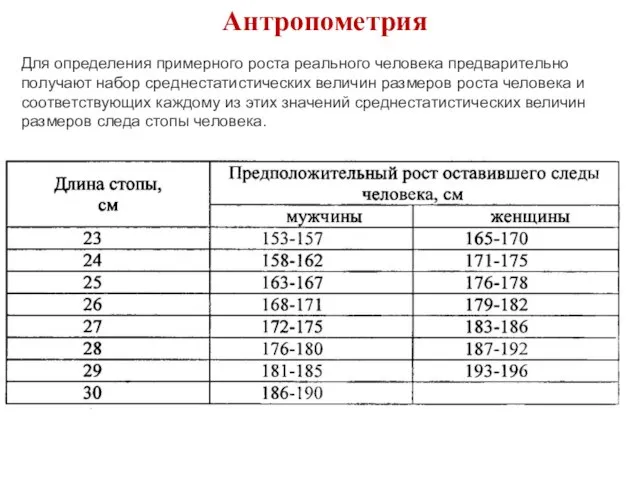
- 61. Антропометрия Рост людей
- 62. Антропометрия Для определения примерного роста реального человека предварительно получают набор среднестатистических величин размеров роста человека и
- 63. Лабораторная работа: Часть 1. Антропометрия. Построить зависимость размера обуви от роста студентов в группе и аппроксимировать
- 65. Скачать презентацию













































 Функция
Функция Геометрия. Это полезно знать
Геометрия. Это полезно знать Презентация на тему Задачи на уменьшение (3 класс)
Презентация на тему Задачи на уменьшение (3 класс)  Действия с десятичными дробями. Интерактивный тренажёр
Действия с десятичными дробями. Интерактивный тренажёр 7fc414894c174883ad06309edf2012ca (1)
7fc414894c174883ad06309edf2012ca (1) Состав числа 11
Состав числа 11 Показательная функция, её свойства и график. Логарифмическая функция, ее свойства и график
Показательная функция, её свойства и график. Логарифмическая функция, ее свойства и график Линейные дискретные системы с постоянными параметрами. Лекция 6
Линейные дискретные системы с постоянными параметрами. Лекция 6 Взвешенные графы. Остовные деревья. Кратчайшие пути
Взвешенные графы. Остовные деревья. Кратчайшие пути Свойство биссектрисы угла
Свойство биссектрисы угла Углы
Углы Вычитание в пределах 20
Вычитание в пределах 20 Табличные случаи сложения и вычитания с переходом через разряд в пределах 20
Табличные случаи сложения и вычитания с переходом через разряд в пределах 20 Планиметрия. Задание 6
Планиметрия. Задание 6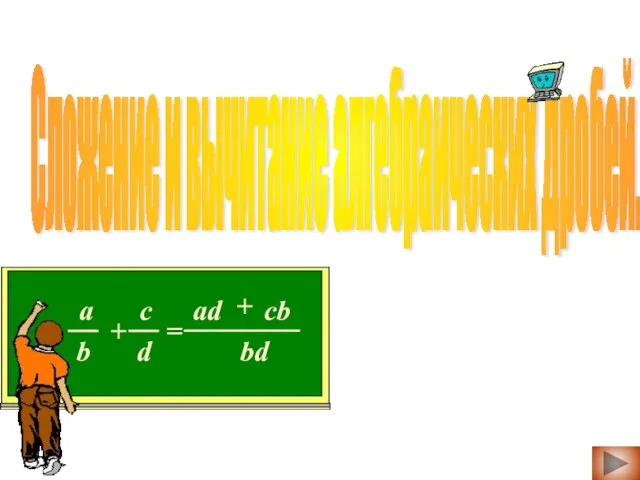 Сложение и вычитание алгебраических дробей
Сложение и вычитание алгебраических дробей Курс по математике ОГЭ 2021
Курс по математике ОГЭ 2021 Задания по уровням. Проверь себя
Задания по уровням. Проверь себя Многогранники. Вершины, рёбра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники. Теорема Эйлера
Многогранники. Вершины, рёбра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники. Теорема Эйлера Единица массы - килограмм
Единица массы - килограмм Пчелки-труженицы. Примеры
Пчелки-труженицы. Примеры Відсоткі
Відсоткі Применение теоремы Пифагора
Применение теоремы Пифагора Мишка. Тренажёр - раскраска
Мишка. Тренажёр - раскраска Решение заданий ЕГЭ. Урок-консультация. 11 класс
Решение заданий ЕГЭ. Урок-консультация. 11 класс Великолепная пятерка. Математический калейдоскоп
Великолепная пятерка. Математический калейдоскоп Презентация на тему Решение задач на готовых чертежах. Площади фигур выполнена в powerpoint
Презентация на тему Решение задач на готовых чертежах. Площади фигур выполнена в powerpoint  Определители матриц
Определители матриц Линейная функция
Линейная функция