Теория множеств

ЛЕКЦИЯ 1
ТЕОРИЯ МНОЖЕСТВ

ГЕОРГ КАНТОР (1845 - 1918)
немецкий математик, логик, теолог, основоположник теории
множеств.
«Множество есть
многое, мыслимое нами
как единое»

ПОНЯТИЕ МНОЖЕСТВА
Множество – это совокупность различимых между собой объектов, объединяемых в целое некоторым общим признаком.
Объекты, из которых состоит множество, называются его элементами.
Обозначения:
A, B, C, … - множества,
а, b, c, … - элементы множества.

ОПРЕДЕЛЕНИЯ, ТЕРМИНЫ И СИМВОЛЫ
Принадлежность:
- элемент принадлежит
множеству
- элемент не принадлежит
множеству

ОПРЕДЕЛЕНИЯ, ТЕРМИНЫ И СИМВОЛЫ
Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается Ø.

ОПРЕДЕЛЕНИЯ, ТЕРМИНЫ И СИМВОЛЫ
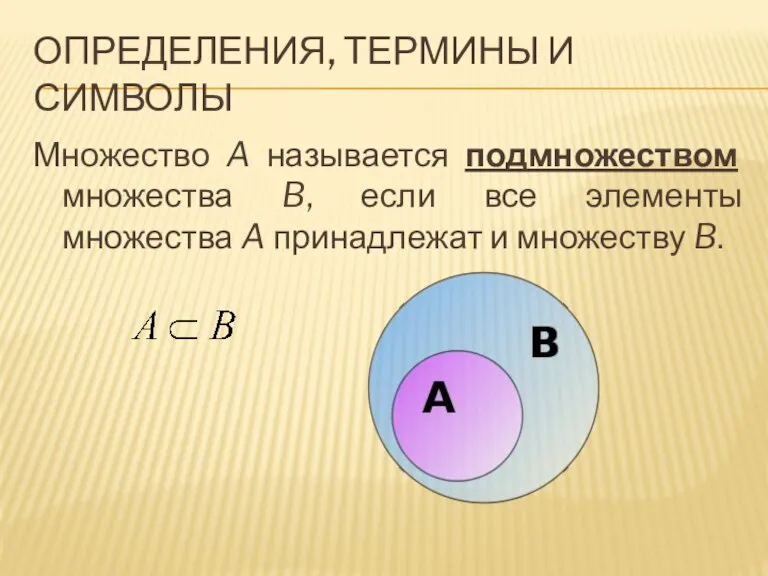
Множество A называется подмножеством множества B, если все элементы множества A принадлежат и множеству B.

СВОЙСТВА ПОДМНОЖЕСТВ
1. Пустое множество является подмножеством любого множества.
2. Множество A является своим подмножеством,
т.е. .
(1) и (2) называют несобственными подмножествами.
4. Если и , то .
5. Если и , то А – собственное подмножество B, т.е. .

ПРИМЕРЫ
1. Дано множество , то его подмножества:
Ø, - несобственные подмножества,
, - собственные подмножества.
2. Пусть A – множество четных чисел, B – множество целых чисел, С – множество нечетных чисел. Тогда

СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВ
1. Перечислением элементов множеств
2. Указанием свойств элементов множества

ПРИМЕР_1
Задать перечислением элементов множество букв, составляющих слово
«СТАТИСТИКА»

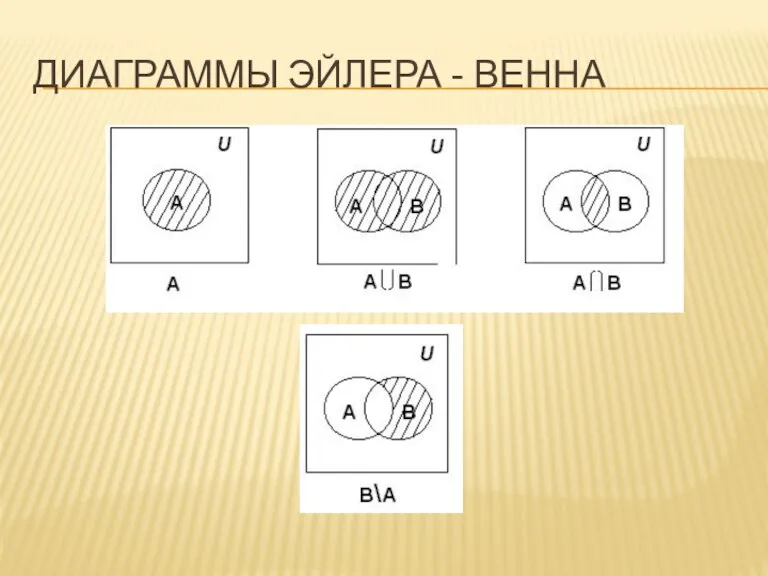
ОБЪЕДИНЕНИЕ МНОЖЕСТВ
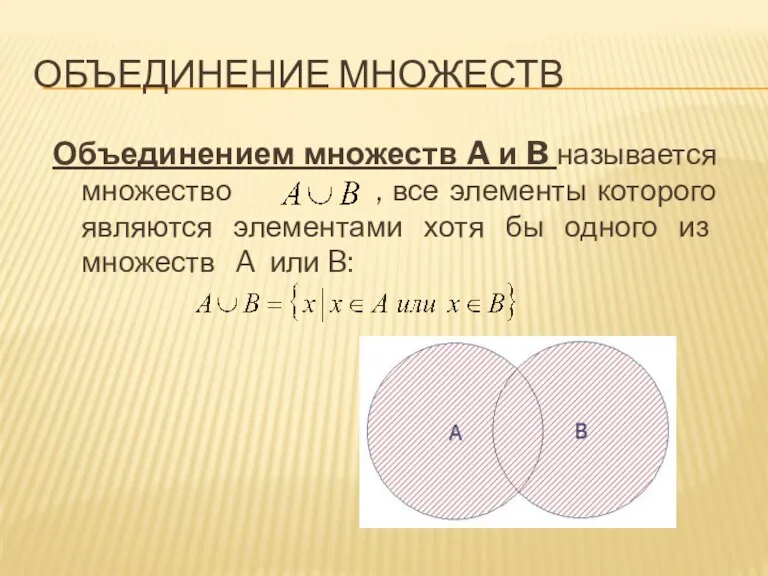
Объединением множеств A и B называется множество , все элементы которого являются элементами хотя бы одного из множеств A или B:

ПРИМЕРЫ
1. Пусть , . Найти .
Решение.
2. Пусть A – множество чисел, которые делятся на 2, а В – множество чисел, которые делятся на 3.
Найти .
Решение.

ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ
Пересечением множеств A и B называется множество , все элементы которого являются элементами обоих множеств A и B одновременно:

ПРИМЕРЫ
1. Пусть , . Найти .
Решение.
2. Пусть A – множество чисел, которые делятся на 2, а В – множество чисел, которые делятся на 3.
Найти .
Решение.

ПРИМЕРЫ
3. Пусть , , .
Найти .
Решение.
Ø

РАЗНОСТЬ МНОЖЕСТВ
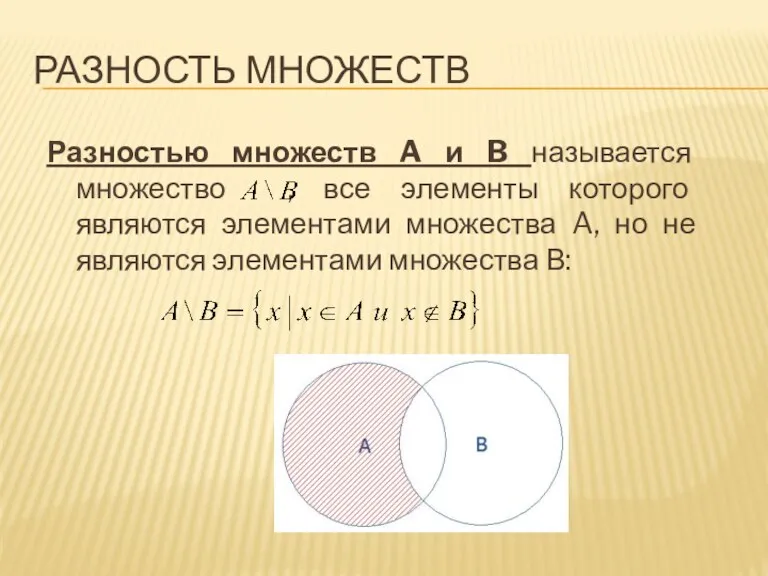
Разностью множеств A и B называется множество , все элементы которого являются элементами множества A, но не являются элементами множества В:

ПРИМЕРЫ
1. Пусть , . Найти , .
Решение.
2. Пусть A – множество чисел, которые делятся на 2, а В – множество чисел, которые делятся на 3.
Найти , .
Решение.

ДИАГРАММЫ ЭЙЛЕРА - ВЕННА

ПРИМЕРЫ
1. Проиллюстрировать на диаграммах Эйлера –Венна результат выполнения операций над множествами:
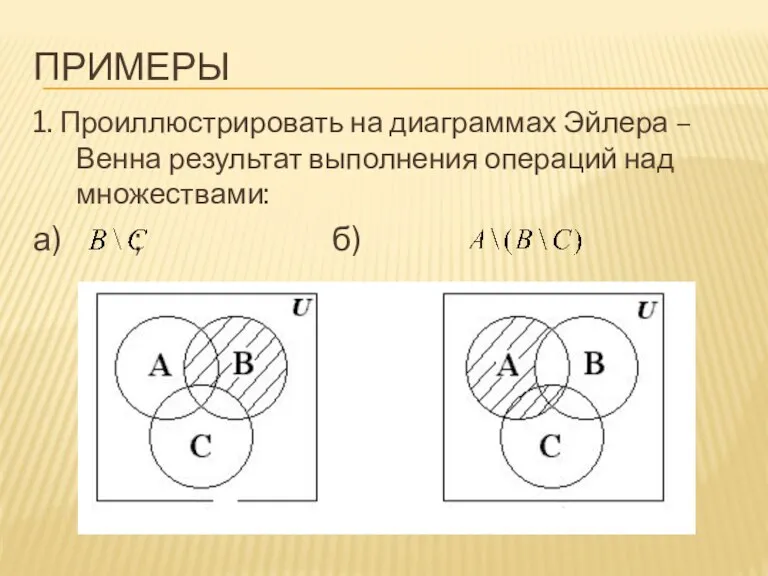
а) ; б)

ПРИМЕРЫ
1. Проиллюстрировать на диаграммах Эйлера –Венна результат выполнения операций над множествами:
в) ; г)