Математика в профессиональной деятельности педагога дошкольного образования. Теория множеств

Теория множеств

План:
Вопрос 1. Множество. Виды множеств.
Вопрос 2. Операции над множествами.
Вопрос 3. Мощность множества

Вопрос 1.
Множество. Виды множеств.

Понятие множества
Понятие множества является одним из фундаментальных понятий математики.
Оно было введено в математику создателем теории множеств немецким ученым Георгом Кантором (1845 – 1918).
Следуя ему, под множеством понимается совокупность объектов произвольной природы, которая рассматривается как единое целое. Объекты, входящие в состав множества, называются его элементами.

Множество
это совокупность объектов (элементов), которые понимаются как единое целое (по тем или иным признакам, критериям или обстоятельствам). Причём, это не только материальные объекты, но и буквы, цифры, теоремы, мысли, эмоции и т.д.
Множества принято обозначать прописными буквами латинского алфавита: A, B, C, …

Для числовых множеств используются следующие обозначения:
N – множество натуральных чисел;
N0 – множество неотрицательных целых чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
I – множество иррациональных чисел;
R – множество действительных чисел;
C – множество комплексных чисел.
Элементы множества обозначаются строчными латинскими буквами: a, b, c, … и записываются в фигурных скобках {}

Пример множеств
А = {а, б, в …я} - множество букв русского алфавита;
N = {1, 2, 3, 4 …} – множество натуральных чисел.
Множества А является конечным (состоящими из конечного числа элементов), а множество N – это пример бесконечного множества.
в теории и на практике рассматривается так называемое пустое множество: – множество, в котором нет ни одного элемента.
принадлежность элемента множеству записывается значком ∈.

Пример множеств
5 ∈ N – число 5 принадлежит множеству натуральных чисел;
5,5 ∈ N – число 5,5 не принадлежит множеству натуральных чисел.

Подмножества
Множество B называется подмножеством множества A, если каждый элемент множества B принадлежит множеству A.
Иными словами, множество В содержится во множестве А и записывается как: В ⊆ А. Данный знак называется знаком включения.
Отношения между подмножествами удобно изображать с помощью условной геометрической схемы, которая называется кругами Эйлера.

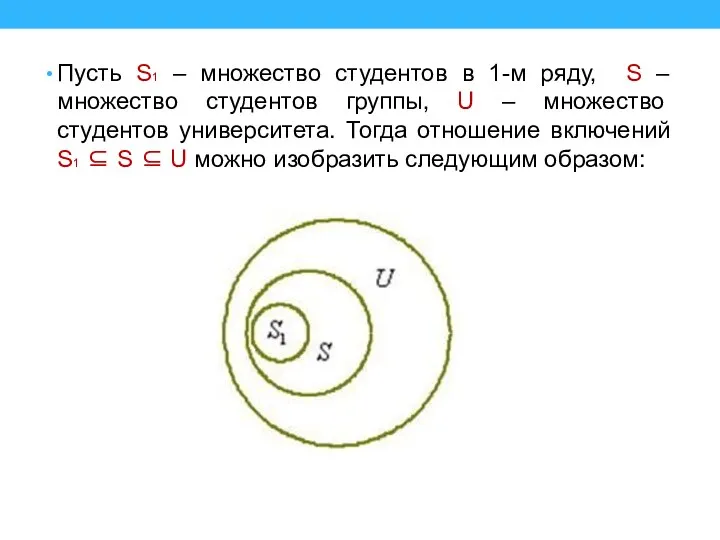
Пусть S1 – множество студентов в 1-м ряду, S – множество студентов группы, U – множество студентов университета. Тогда отношение включений S1 ⊆ S ⊆ U можно изобразить следующим образом:

Вопрос 2.
Операции над множествами

Действия над множествами. Диаграммы Венна
Диаграммы Венна (по аналогии с кругами Эйлера) – это схематическое изображение действий с множествами.
Операции над множествами могут быть следующими:
Пересечение (конъюнкция) или логическое умножение.
Объединение (дизъюнкция) или логическое сложение.
Разность множеств.

Пересечение (конъюнкция) или логическое умножение
Пересечение множеств характеризуется логической связкой И, обозначается знаком ∩
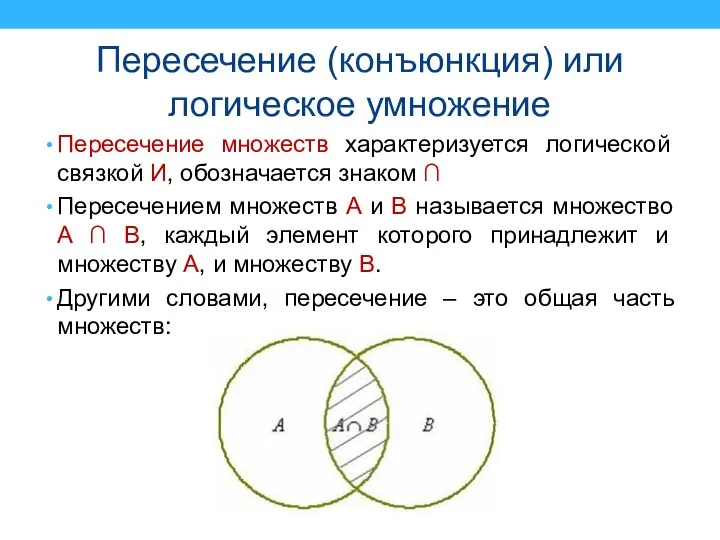
Пересечением множеств А и В называется множество A ∩ B, каждый элемент которого принадлежит и множеству А, и множеству В.
Другими словами, пересечение – это общая часть множеств:

Объединение (дизъюнкция) или логическое сложение
Объединение множеств характеризуется логической связкой ИЛИ и обозначается значком ∪
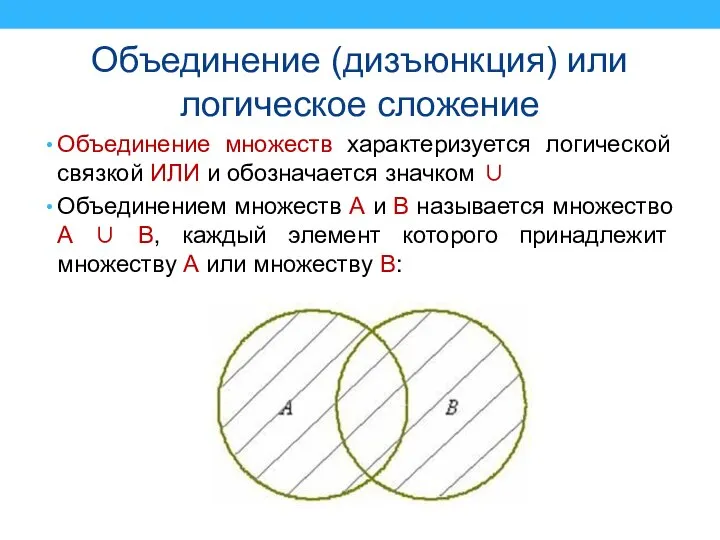
Объединением множеств А и В называется множество A ∪ B, каждый элемент которого принадлежит множеству А или множеству В:

Разность множеств
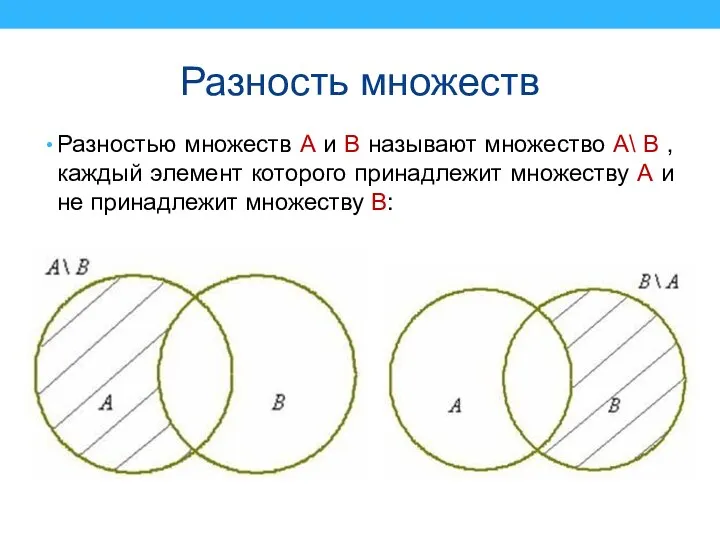
Разностью множеств А и В называют множество А\ В , каждый элемент которого принадлежит множеству А и не принадлежит множеству В:

Вопрос 3.
Мощность множества