Матрицы

Матрицей называется прямоугольная
таблица чисел .
Если матрица содержит строк и
столбцов, то говорят, что матрица имеет
размерность .
- порядок матрицы

Обозначение матриц

Матрица размера m×m называется
квадратной.
Матрица , имеющая только одну строку
называется матрицей-строкой.
Матрица, имеющая только один
столбец называется
матрицей-столбцом .

Две матрицы считаются равными,
если равны их размеры и равны
элементы, стоящие на одинаковых
местах.
Квадратная матрица называется
невырожденной (неособенной), если
её определитель отличен от нуля, и
вырожденной (особенной) , если
определитель её равен нулю.

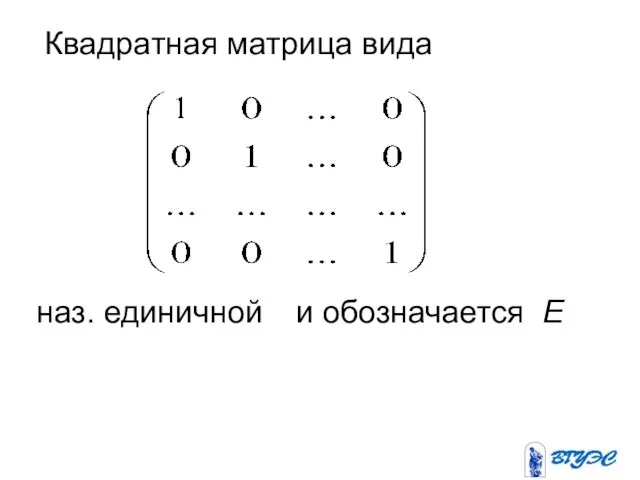
Квадратная матрица вида
наз. единичной и обозначается Е

Матрица, все элементы которой равны нулю, наз. нулевой.
Определитель, составленный из элементов квадратной матрицы, наз. определителем матрицы.
Очевидно

Матрица
наз. транспонированной по отношению к
матрице

Действия над матрицами.
Суммой двух матриц одинаковой
размерности А и В называется
матрица С той же размерности,
элементы которой равны суммам
элементов матриц A и B с
одинаковыми индексами.

Произведением матрицы на
число α называется матрица ,
получающаяся из матрицы A
умножением всех её элементов
на α .

Разностью двух матриц А и В
одинаковой размерности
называется матрица С=A+(-B).

Произведением матрицы
размера на матрицу
размера
называется матрица размера
, элемент которой , стоящий в i-ой строке и j-ом столбце, равен
сумме произведений элементов i-ой
строки матрицы A и соответствующих
элементов j-го столбца матрицы B.

Свойства операций над
матрицами
1.A+B=B+A
2.(A+B)+C=A+(B+C)
3.(A+B)k=kA+kB

4. (AB)C=A(BC)
5. A(B+C)=AB+AC
6. A+O=A
7. AE=EA=A

Если и две квадратные матрицы одного порядка, то

Обратная матрица

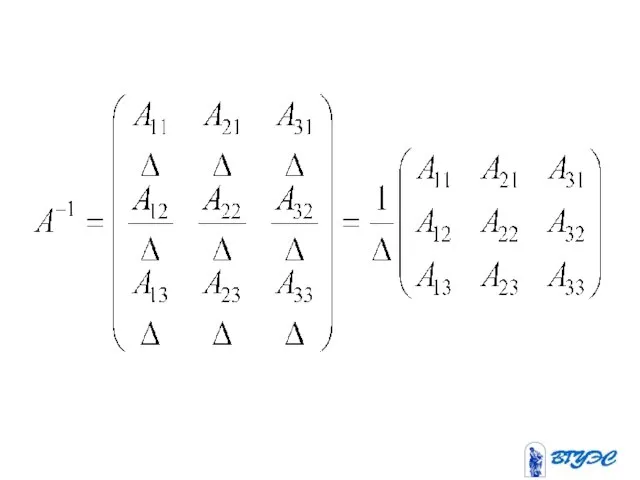
Пусть - квадратная матрица.
Обратной для неё матрицей наз.
квадратная матрица того же порядка,
обозначаемая и
удовлетворяющая условию

Для того, чтобы квадратная матрица
имела обратную матрицу, необходимо и
достаточно, чтобы матрица была
невырожденной.

Р а н г м а т р и ц ы
Рангом матрицы называется наивысший
из порядков отличных от нуля миноров
матрицы.
Ранг матрицы A обозначается:
или .

Теорема о ранге матрицы
Ранг матрицы равен
максимальному числу линейно –
независимых строк матрицы.

Элементарные преобразования матрицы.
1.Умножение всех элементов строк на одно и то же число не равное 0.
2. Перестановка строк местами.
3. Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на одно и тоже число.

4.Отбрасывание одной из двух одинаковых строк.
5.Отбрасывание нулевой строки