Слайд 3Вопросы для повторения
. Что называют криволинейной 1трапецией?
2. Являются ли фигуры, изображённые на

графиках криволинейными трапециями?
3. Запишите формулу для вычисления площади криволинейной трапеции
Слайд 4Рассмотрим другой подход к вычислению площади криволинейной трапеции
Будем считать функцию f неотрицательной

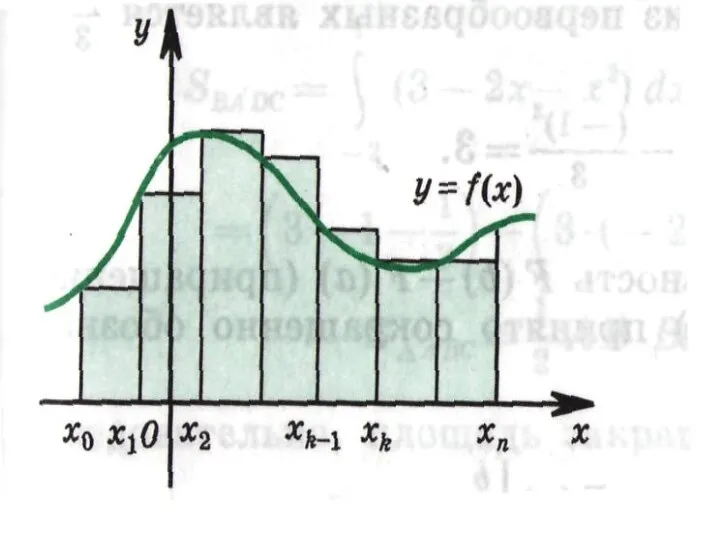
и непрерывной на отрезке [а; в], тогда площадь S соответствующей криволинейной трапеции можно приближённо подсчитать следующим образом
Слайд 6Разобьём отрезок [а; в] на n отрезков одинаковой длины точками
![Разобьём отрезок [а; в] на n отрезков одинаковой длины точками](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/945473/slide-5.jpg)
Слайд 7 При n → ∞
Sn→ к некоторому числу
Это число называют интегралом

функции f от а до в и обозначают:
в
∫ f(х)dх
а
Слайд 8 Числа а и в - называются пределами
интегрирования, а –

нижним пределом, в – верхним.
Знак ∫ - называют знаком интеграла
Функцию f называют подынтегральной функцией, а переменная х – переменной интегрирования
df- знак дифференциала
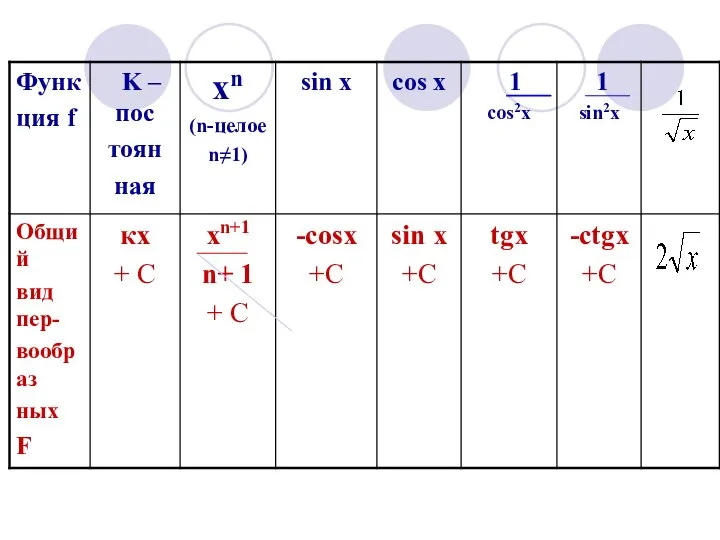
Слайд 9 Итак, если f( х ) ≥0 на отрезке [а; в], то
![Итак, если f( х ) ≥0 на отрезке [а; в], то Площадь](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/945473/slide-8.jpg)
Площадь соответствующей криволинейной трапеции выражается формулой:
в
S = ∫ f(х)dх
а
Слайд 10Сравнивая формулы криволинейных трапеций :
в
S = ∫ f(х)dх и S

= F(в) – F(а)
а
Делаем вывод:
Слайд 12Иссак Ньютон
(1643-1716)
Готфрид
Лейбниц(1646-1716).




![Разобьём отрезок [а; в] на n отрезков одинаковой длины точками](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/945473/slide-5.jpg)


![Итак, если f( х ) ≥0 на отрезке [а; в], то Площадь](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/945473/slide-8.jpg)



 Теория фракталов
Теория фракталов Арифметический корень степени п
Арифметический корень степени п Применение производной для исследования функций на монотонность
Применение производной для исследования функций на монотонность Посади воздушные шары. Математика
Посади воздушные шары. Математика Деление десятичных дробей
Деление десятичных дробей Упрощение выражений. Игра, 6 класс
Упрощение выражений. Игра, 6 класс Подготовка к ГИА Решение задач по теории вероятностей
Подготовка к ГИА Решение задач по теории вероятностей Презентация на тему Ромб
Презентация на тему Ромб  Приближенные вычисления
Приближенные вычисления Площадь треугольника
Площадь треугольника Корреляция. Показатель корреляции
Корреляция. Показатель корреляции Состав чисел в приделах 10. Решение задач
Состав чисел в приделах 10. Решение задач Развитие пространственного мышления младших школьников не основе конструирования. Оригами
Развитие пространственного мышления младших школьников не основе конструирования. Оригами Понятия возрастающей и убывающей функций. Понятие монотонности функции. Возрастание и убывание функции
Понятия возрастающей и убывающей функций. Понятие монотонности функции. Возрастание и убывание функции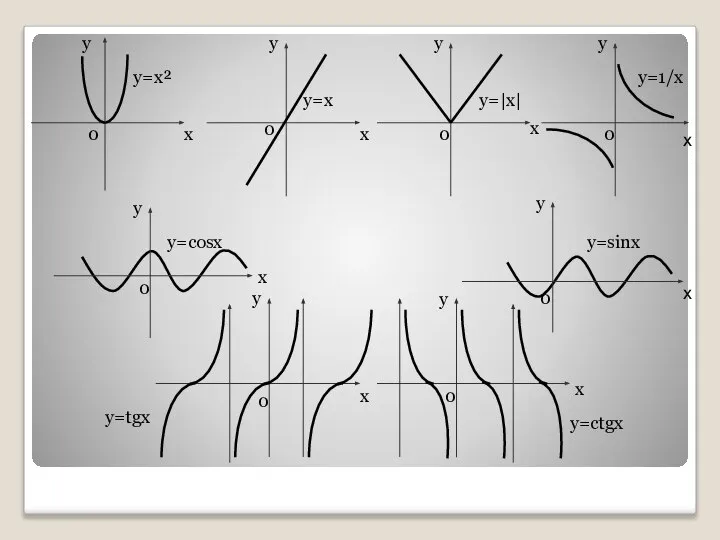 Параллельный перенос вдоль оси координат
Параллельный перенос вдоль оси координат Процент. Сорауларга җавап бирегез
Процент. Сорауларга җавап бирегез Развертка. Создание объёмных фигур из плоскости
Развертка. Создание объёмных фигур из плоскости Формула Пика
Формула Пика Логарифмические уравнения
Логарифмические уравнения Дифференциальные уравнения и их применение в медицинской практике. Элементы комбинаторики. Случайные величины
Дифференциальные уравнения и их применение в медицинской практике. Элементы комбинаторики. Случайные величины Формулы. Урок 1
Формулы. Урок 1 Параллелограмм и трапеция. Урок 8
Параллелограмм и трапеция. Урок 8 Это полезно знать. Интересные факты из жизни самых больших чисел
Это полезно знать. Интересные факты из жизни самых больших чисел Действия с обыкновенными дробями. Подготовка к ОГЭ задания первой части 1, 3, 8
Действия с обыкновенными дробями. Подготовка к ОГЭ задания первой части 1, 3, 8 Вычисления вида 32 + 8, 40 – 8
Вычисления вида 32 + 8, 40 – 8 Развитие общества по закону синусоиды. Понятие Графика функции y=sin x
Развитие общества по закону синусоиды. Понятие Графика функции y=sin x Kombinatorika
Kombinatorika Измерительные приборы. Виды и предназначение
Измерительные приборы. Виды и предназначение