Матрицы и действия над ними

1. Определение матрицы
Прямоугольная таблица чисел вида
называется матрицей.
- элементы матрицы.
Размер матрицы
Главная диагональ матрицы
Побочная диагональ матрицы
назад

2. Виды матриц
Прямоугольная
Квадратная
Нулевая
Единичная
Диагональная
Симметричная
Вырожденная
Равные
Треугольная
Квазитреугольная (ступенчатая или трапециевидная)
Матрица-строка или строчная матрица
Матрица-столбец или столбцевая матриц
назад

Матрица называется прямоугольной, если количество ее строк не совпадает с количеством столбцов:
Матрица называется квадратной, если количество ее строк совпадает с количеством столбцов:
назад

Матрица называется нулевой, если все ее элементы нулевые :
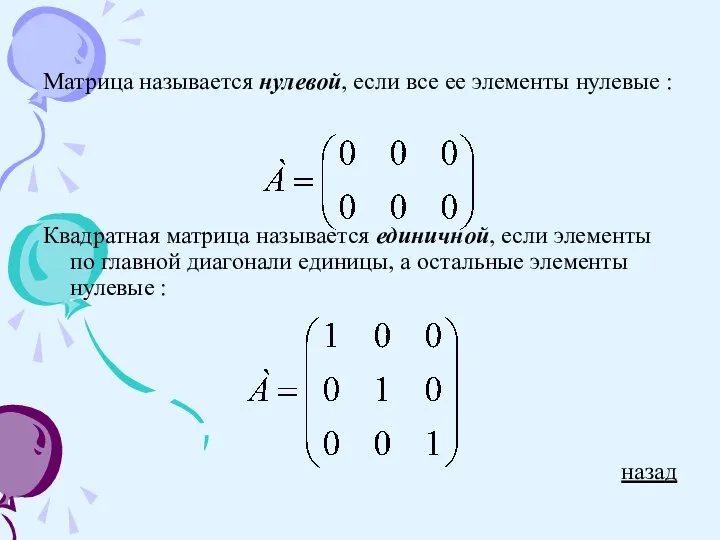
Квадратная матрица называется единичной, если элементы по главной диагонали единицы, а остальные элементы нулевые :
назад

Квадратная матрица называется диагональной, если элементы по главной диагонали отличны от нуля, а остальные элементы нулевые:
Квадратная матрица называется симметричной, если относительно главной диагонали для всех ее элементов выполняется условие :
назад

Квадратная матрица называется вырожденной, если ее определитель равен нулю.
Матрицы А и В (одинаковых размерностей) называются равными, если :
назад

Квадратные матрицы вида
или
называются треугольными.
назад

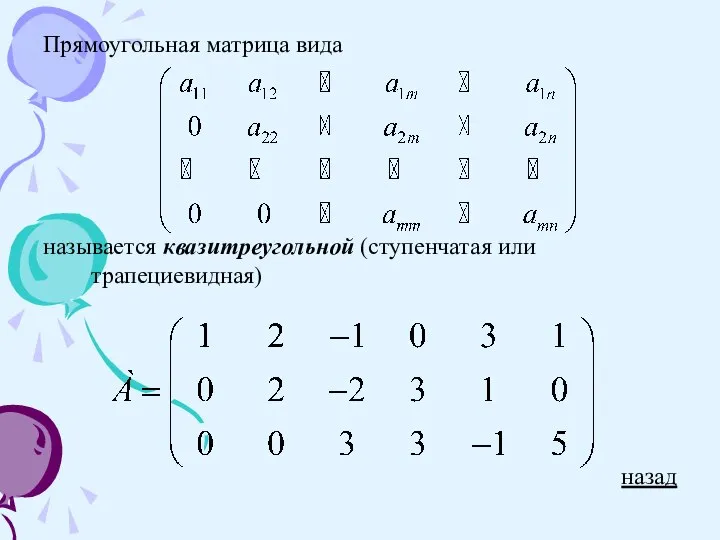
Прямоугольная матрица вида
называется квазитреугольной (ступенчатая или трапециевидная)
назад

Матрица, состоящая из одной строки называется матрицей-строкой или строчной матрицей.
Матрица, состоящая из одного столбца называется матрицей-столбцом или столбцевой матрицей
назад

назад

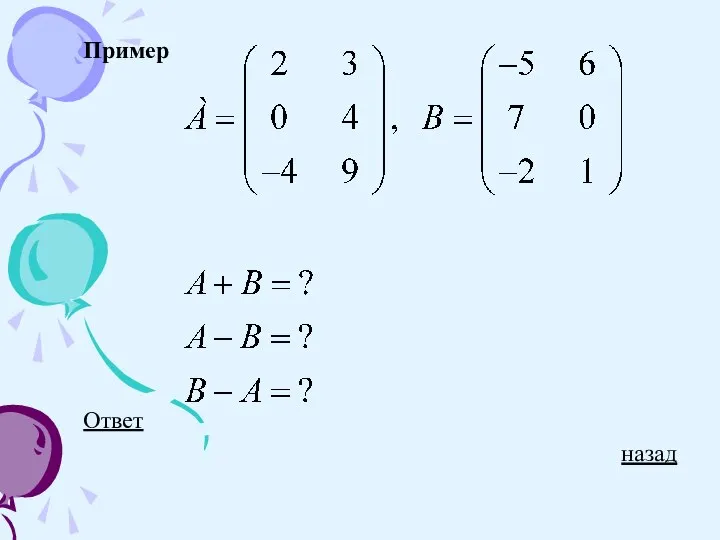
Суммой (разностью) двух матриц одинаковой размерности называется матрица, элементы которой равны сумме (разности) соответствующих элементов матриц слагаемых.
Например:
Пример
назад

Пример
Ответ
назад

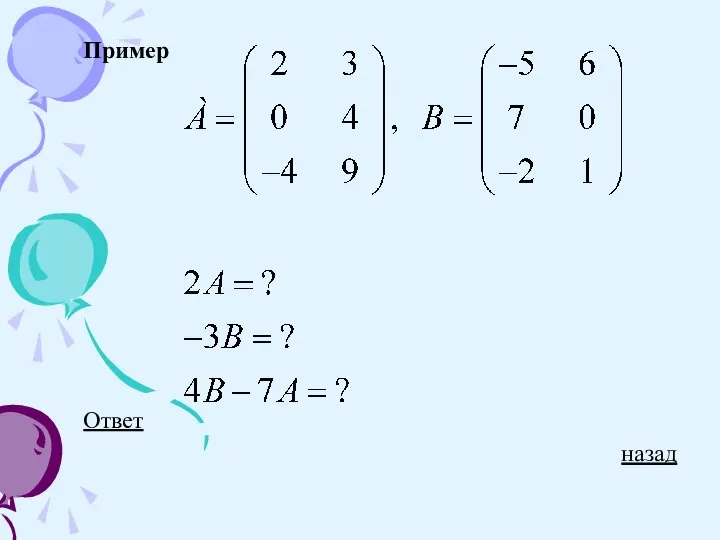
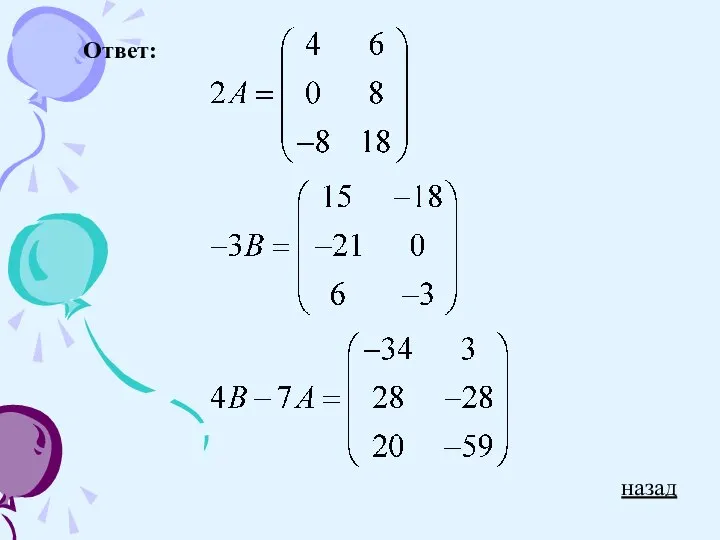
Произведением матрицы на число называется матрица, полученная из данной умножением всех ее элементов на число.
Например:
Пример
назад

Линейные операции обладают следующими свойствами:

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной относительно данной.
Например:
Свойства
назад

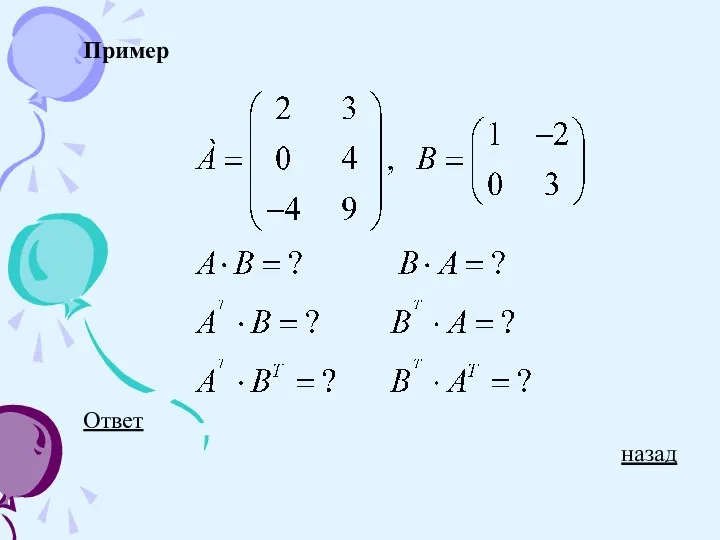
Умножение матриц определяется для согласованных матриц.
Произведением матрицы на матрицу называется матрица , для которой ,
т.е. каждый элемент матрицы С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В.
Например
Свойства
назад

Например:
Пример
назад

В случае, когда АВ=ВА, матрицы А и В называют перестановочными или коммутативными.
Пример 1. Найти все перестановочные матрицы к матрице
Пример 2. Найти все перестановочные матрицы к матрице
назад

Ответ:
назад

Пример
Ответ
назад

Ответ:
назад

Свойства операции транспонирования:
назад

Матрица А называется согласованной с матрицей В, если число столбцов матрицы А равно числу строк матрицы В:
Например:
назад

Пример
Ответ
назад

Ответ:
назад

Свойства операции умножение матриц:
1. Свойство сочетательности или ассоциативности
2.
Свойство распределительности (дистрибутивности) справа и слева относительно сложения матриц
назад

Решение (Пример 1):
1) общий вид всех перестановочных матриц
2) Применим определение перестановочных матриц AB=BA:

Получаем:
3) По определению равных матриц
4) Общий вид всех перестановочных матриц
5) Проверка
назад

Ответ:
или
или
назад