Содержание
- 2. Problem Definition Given an undirected graph G(V,E), find a cut between the vertices, such that the
- 3. Max Cut is NP-Hard! We show that it is NP-Hard by a reduction from the NAE-3-SAT
- 4. NAE-3-SAT Problem Not All Equal-3-SAT: A circuit consisting of a big AND of clauses Each clause
- 5. The Reduction – Step 0 Max Cut ∈ NP Change problem to: “Is there a cut
- 6. The Reduction – Step 1 What to reduce it to? Reduce to NAE-3-SAT NAE-3-SAT ≤ Max
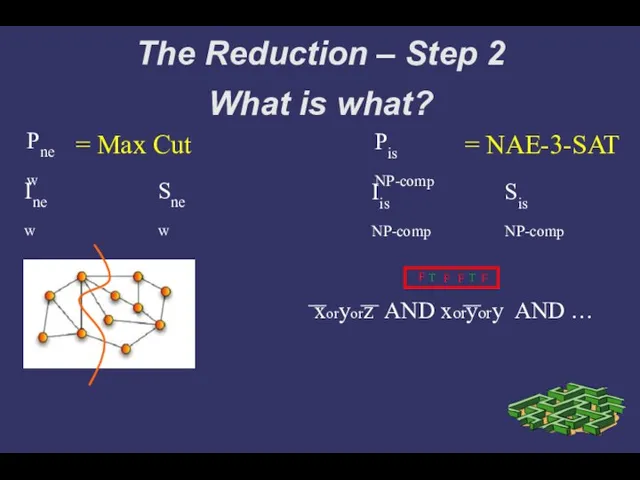
- 7. The Reduction – Step 2 What is what? = Max Cut = NAE-3-SAT Pnew Pis NP-comp
- 8. The Reduction – Step 3 Direction of Reduction and Code Want to show that Max Cut
- 9. The Reduction – Step 4 Look for Similarities Max Cut NAE-3-SAT Literals x y z ¬x
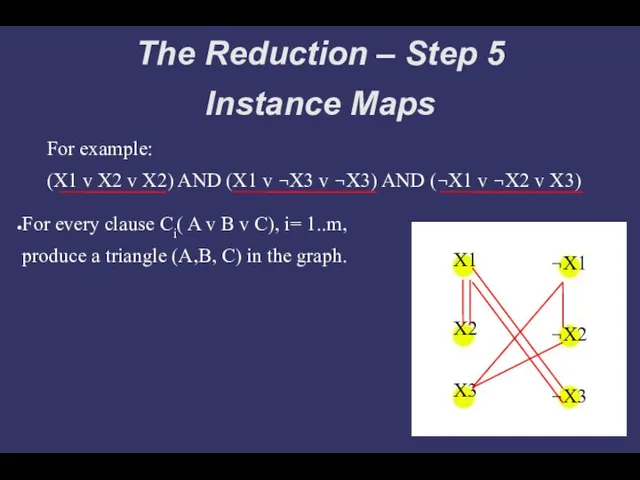
- 10. The Reduction – Step 5 Instance Maps For every clause Ci( A v B v C),
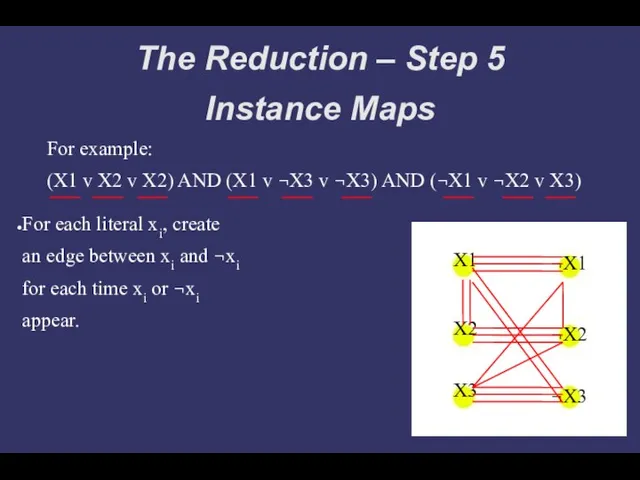
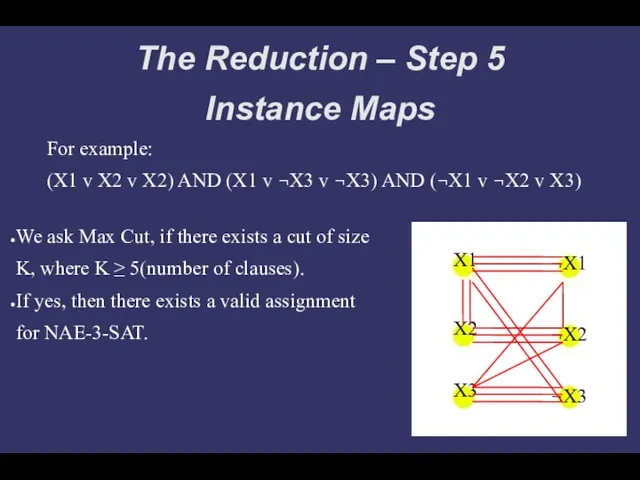
- 11. The Reduction – Step 5 Instance Maps For example: (X1 v X2 v X2) AND (X1
- 12. The Reduction – Step 5 Instance Maps For example: (X1 v X2 v X2) AND (X1
- 13. The Reduction – Step 5 Instance Maps For example: (X1 v X2 v X2) AND (X1
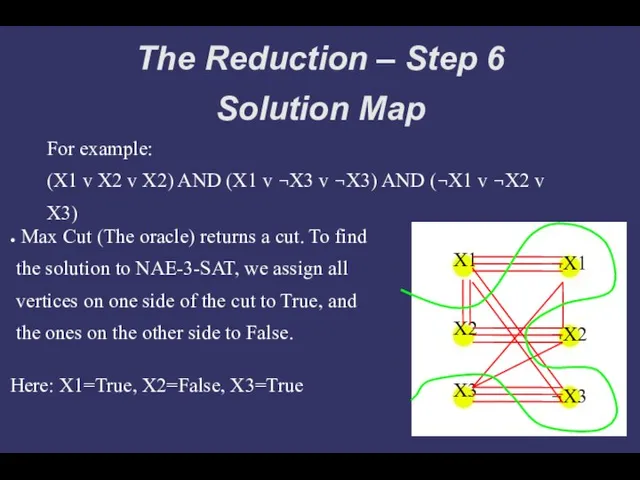
- 14. The Reduction – Step 6 Solution Map For example: (X1 v X2 v X2) AND (X1
- 15. The Reduction – Step 7 Valid to Valid X1 X2 X3 ¬X1 ¬X2 ¬X3 Assume the
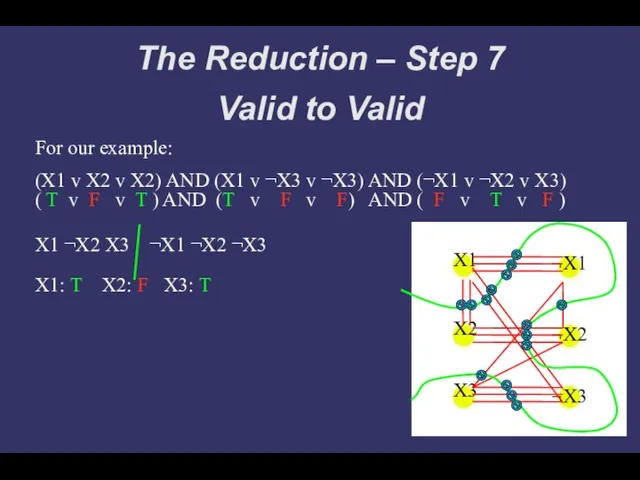
- 16. The Reduction – Step 7 Valid to Valid X1 X2 X3 ¬X1 ¬X2 ¬X3 For our
- 17. The Reduction – Step 7 Valid to Valid X1 X2 X3 ¬X1 ¬X2 ¬X3 All m
- 18. The Reduction – Step 7 Valid to Valid X1 X2 X3 ¬X1 ¬X2 ¬X3 For our
- 19. The Reduction – Steps 8&9 Reverse Solution Map Conversely, it is also possible for a valid
- 20. The Reduction – Step 10 Working Algorithm We now have a working algorithm for the NAE-3-SAT
- 21. The Reduction – Step 11 Running Time? We can create an instance map (clauses -> graph)
- 22. Max Cut – Running Time The best known algorithm for finding an optimal solution for the
- 23. Max Cut – Randomized Algorithm Here is a simple approximation Max Cut Algorithm instead: The cut
- 24. Max Cut – Randomized Algorithm Flip a coin! To see in which of the two sets
- 26. Скачать презентацию

















 Плоскость. Уравнение плоскости по точке и нормальному вектору
Плоскость. Уравнение плоскости по точке и нормальному вектору формулы
формулы Проценты и десятичные дроби
Проценты и десятичные дроби Презентация на тему Элементы теории вероятностей на ЕГЭ
Презентация на тему Элементы теории вероятностей на ЕГЭ  Применение производной. Учебно-тренировочные материалы для подготовки к ЕГЭ
Применение производной. Учебно-тренировочные материалы для подготовки к ЕГЭ Презентация на тему Проценты 5 класс
Презентация на тему Проценты 5 класс  Подготовка к ЕГЭ. Площадь многоугольников
Подготовка к ЕГЭ. Площадь многоугольников Учимся писать цифры
Учимся писать цифры Длина окружности. Площадь
Длина окружности. Площадь Интерактивная игра. Математический футбол
Интерактивная игра. Математический футбол Некоторые свойства прямоугольных треугольников. Задачи на готовых чертежах
Некоторые свойства прямоугольных треугольников. Задачи на готовых чертежах Треугольник
Треугольник Признаки равенства треугольников
Признаки равенства треугольников Скалярное произведение векторов
Скалярное произведение векторов Величины. Свойства величин
Величины. Свойства величин 2_бинарные отношения
2_бинарные отношения Построение графиков функций с помощью геометрических преобразований
Построение графиков функций с помощью геометрических преобразований Треугольники. Решение задач
Треугольники. Решение задач Метод координат в пространстве
Метод координат в пространстве Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Аналитическая геометрия. Поверхности
Аналитическая геометрия. Поверхности Презентация на тему Обыкновенные дроби
Презентация на тему Обыкновенные дроби  Предел функции (часть 4)
Предел функции (часть 4) Функции у=|x| и ей график
Функции у=|x| и ей график Понятие структуры в теории систем. Лекция 4
Понятие структуры в теории систем. Лекция 4 Графическая лаборатория Цель: систематизировать знания по теме «Функции и их графики», закрепить навыки работы с графиками функц
Графическая лаборатория Цель: систематизировать знания по теме «Функции и их графики», закрепить навыки работы с графиками функц Упрощение выражений. Урок-сказка
Упрощение выражений. Урок-сказка Увеличение и уменьшение на несколько %
Увеличение и уменьшение на несколько %