Содержание
- 2. Корни многочлена делят числовую ось на промежутки, на каждом из которых функция сохраняет свой знак без
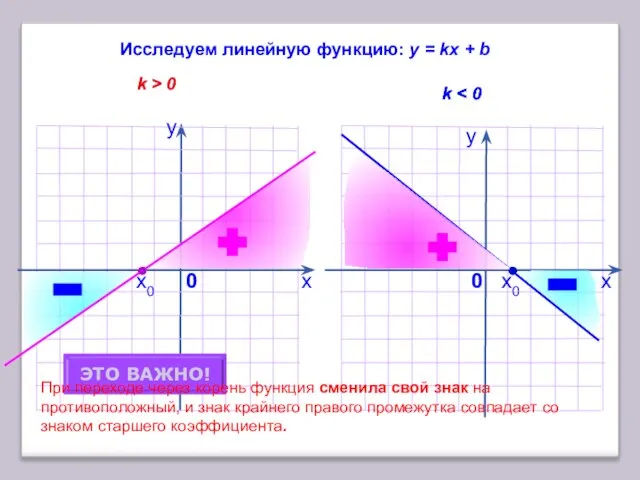
- 3. х у 0 Исследуем линейную функцию: у = kx + b k > 0 k у
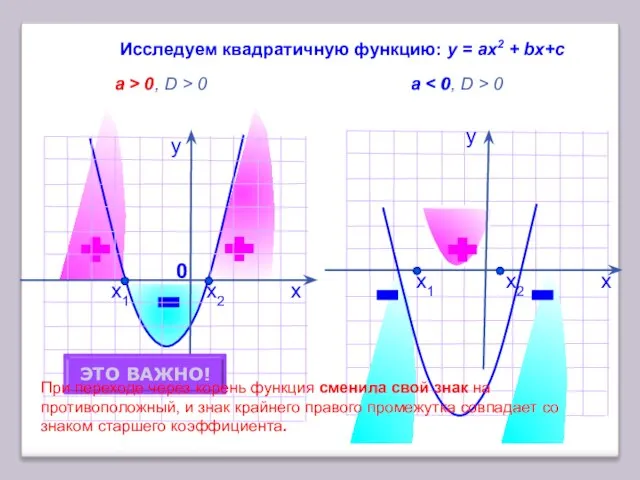
- 4. х у Исследуем квадратичную функцию: у = аx2 + bх+с a > 0, D > 0
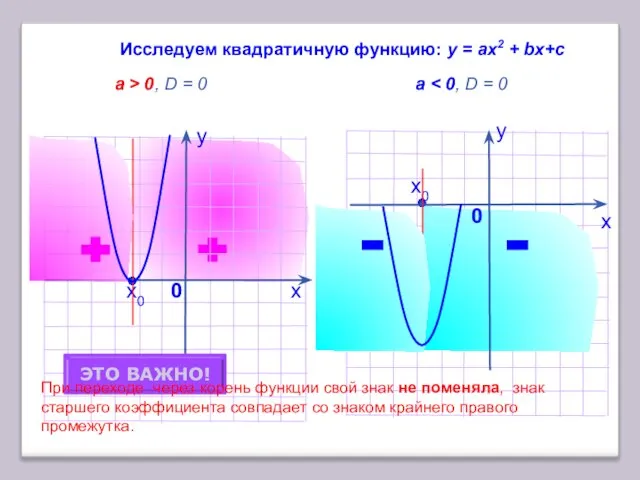
- 5. х Исследуем квадратичную функцию: у = аx2 + bх+с a > 0, D = 0 a
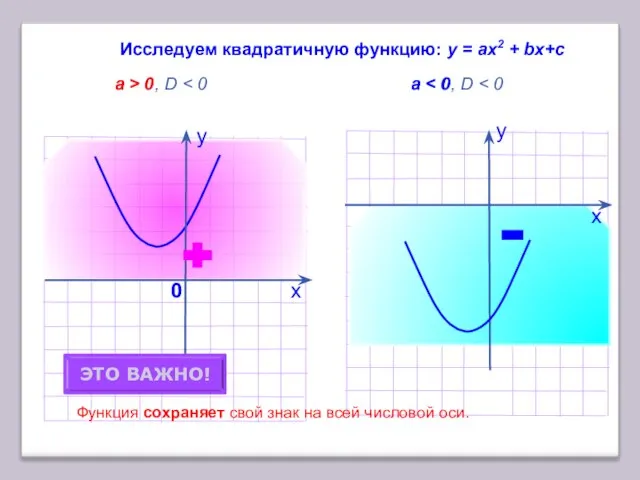
- 6. х Исследуем квадратичную функцию: у = аx2 + bх+с a > 0, D a у 0
- 7. Выводы: 1) если корень функции встречается нечетное число раз, то при переходе через него функция меняет
- 8. Алгоритм решения неравенств методом интервалов: привести неравенство к сравнению многочлена с нулем; найти корни многочлена, для
- 9. Решение неравенств
- 10. - 1 №1. x2 – 3х – 4 ≥ 0 х 4 Неравенство готово для решение
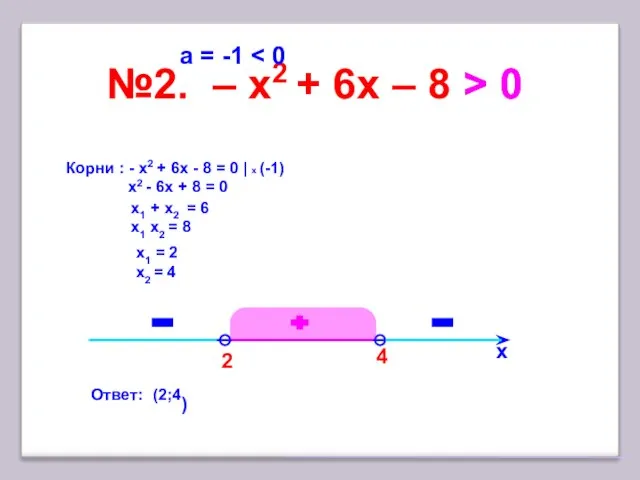
- 11. 2 №2. – x2 + 6х – 8 > 0 х 4 Корни : - x2
- 12. №3. 3x2 ≤ 1 х Корни : 3x2 - 1 = 0 3х2 = 1 х2
- 13. 1 №4. x2 – 2х + 1 > 0 х Корни : x2 – 2х +1
- 14. 3 №8. (x – 3)18 > 0 х Корни : x - 3 = 0 х
- 15. 5 №9. (5 – х)5 ≥ 0 х Корни : 5 - х = 0 х
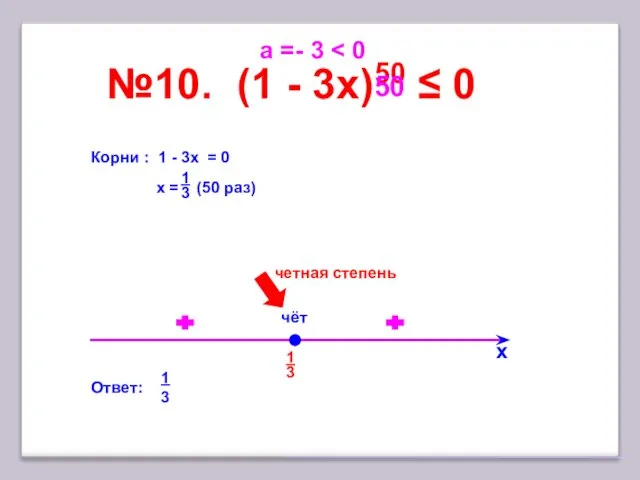
- 16. 1 №10. (1 - 3x)50 ≤ 0 х Корни : 1 - 3x = 0 х
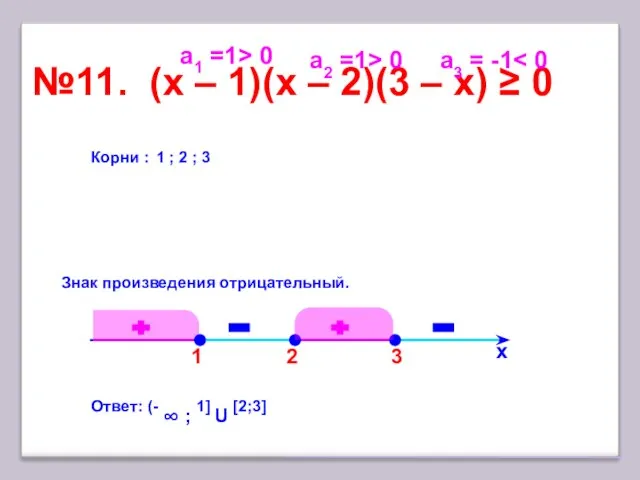
- 17. 3 №11. (x – 1)(х – 2)(3 – х) ≥ 0 х Корни : 1 ;
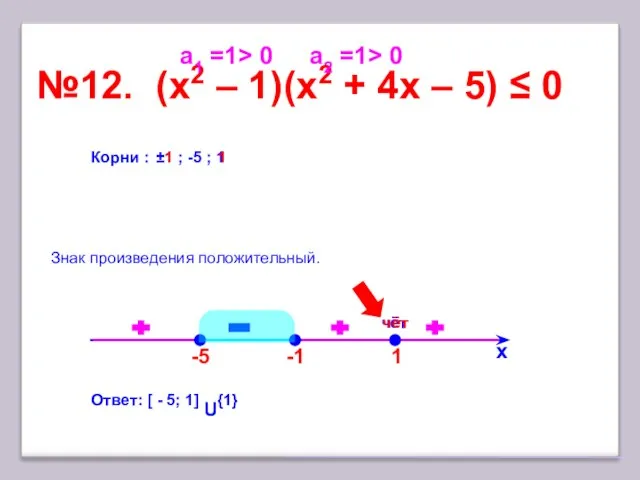
- 18. 1 №12. (x2 – 1)(х2 + 4x – 5) ≤ 0 х Корни : ±1 ;
- 19. 6 №13. х Корни числителя : ± 2 Ответ: [ - 2; 2) U (2; 6)
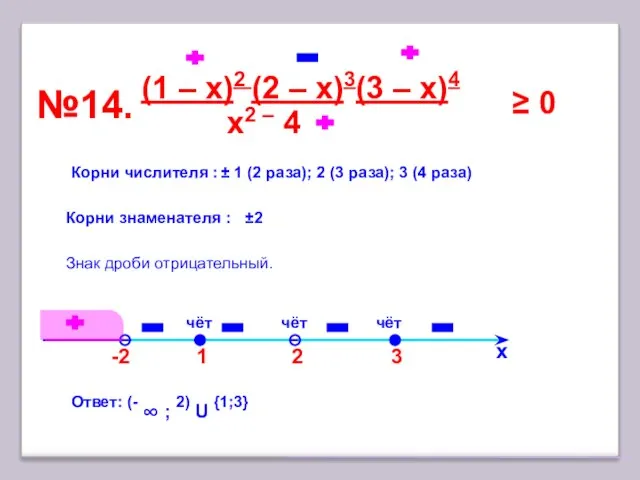
- 20. 3 №14. х Корни числителя : ± 1 (2 раза); 2 (3 раза); 3 (4 раза)
- 22. Скачать презентацию










 Векторная алгебра. Лекция 4
Векторная алгебра. Лекция 4 Презентация на тему Умножение одночленов. Возведение одночленов в степень
Презентация на тему Умножение одночленов. Возведение одночленов в степень  Равенство треугольников
Равенство треугольников Математика. Часть 1
Математика. Часть 1 АЛГОРИТМ ЕВКЛИДА
АЛГОРИТМ ЕВКЛИДА Задача по математике (1 класс, задание 15)
Задача по математике (1 класс, задание 15) Счет в пределах 5
Счет в пределах 5 Перпендикулярные прямые
Перпендикулярные прямые Числовые функции
Числовые функции Математические лабиринты
Математические лабиринты задача про арбузы2
задача про арбузы2 Веселое путешествие
Веселое путешествие Площадь прямоугольника
Площадь прямоугольника Сечение многогранника плоскостью
Сечение многогранника плоскостью Стереометрия. Основные понятия стереометрии. Аксиомы стереометрии
Стереометрия. Основные понятия стереометрии. Аксиомы стереометрии Типовой расчет по дискретной математике
Типовой расчет по дискретной математике Построение сечений
Построение сечений Число и цифра 2
Число и цифра 2 Объём произвольного тела вращения
Объём произвольного тела вращения Презентация на тему Формулы сокращённого умножения
Презентация на тему Формулы сокращённого умножения  Математические методы в психологии. Генеральная совокупность и выборка
Математические методы в психологии. Генеральная совокупность и выборка Квадратичная функция и ее график
Квадратичная функция и ее график Математический тренажёр Наряжаем ёлочку. Случаи сложения и вычитания вида 26+4, 30-7
Математический тренажёр Наряжаем ёлочку. Случаи сложения и вычитания вида 26+4, 30-7 Остроугольный, прямоугольный и тупоугольный треугольники
Остроугольный, прямоугольный и тупоугольный треугольники Решение уравнений
Решение уравнений Диаграммы
Диаграммы Производная и интеграл показательной и логарифмической функций
Производная и интеграл показательной и логарифмической функций Презентация на тему Единицы измерения
Презентация на тему Единицы измерения