Метод интервалов. Общий метод интервалов

Курсы поступления в 9 класс лицея 134

Определение

+
-
+
-
+

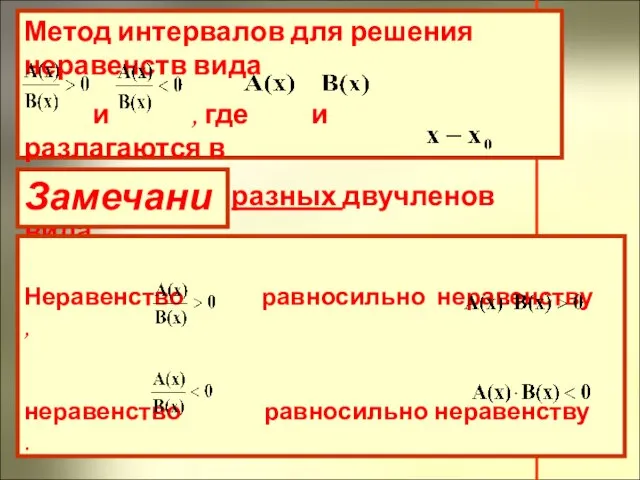
Метод интервалов для решения неравенств вида
, , , ,
где , ,
, то есть все различны.

3. Над промежутком справа от наибольшего нуля многочлена поставить знак «+», так как на этом промежутке все множители положительны. Затем, двигаясь справа налево, при переходе через очередной нуль, сменить знак на противоположный.

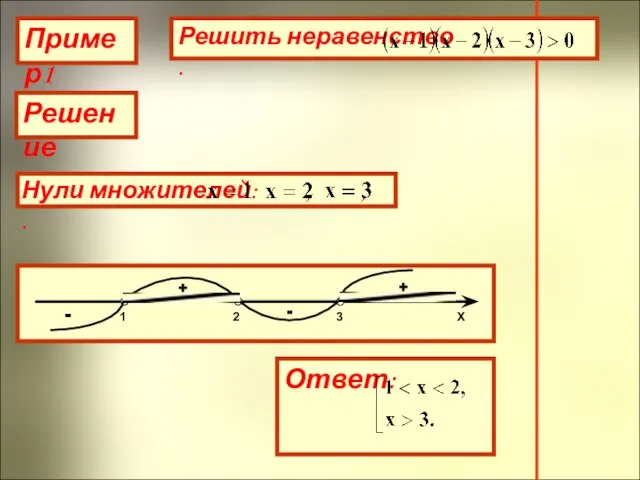
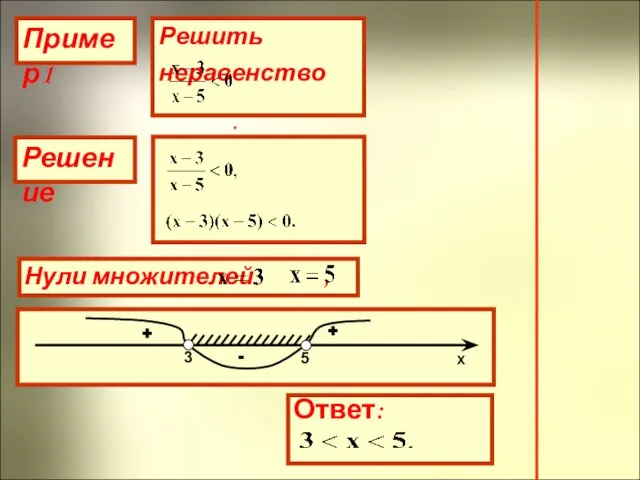
Пример1
Решение
+
-
+
-

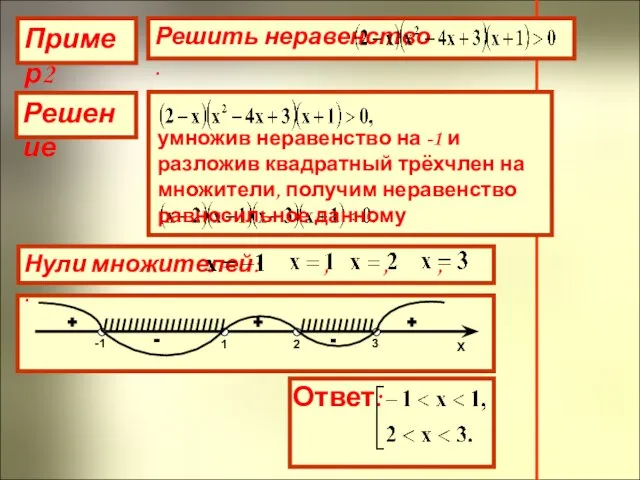
Пример2
Решение
умножив неравенство на -1 и разложив квадратный трёхчлен на множители, получим неравенство равносильное данному
+
-
+
-
+

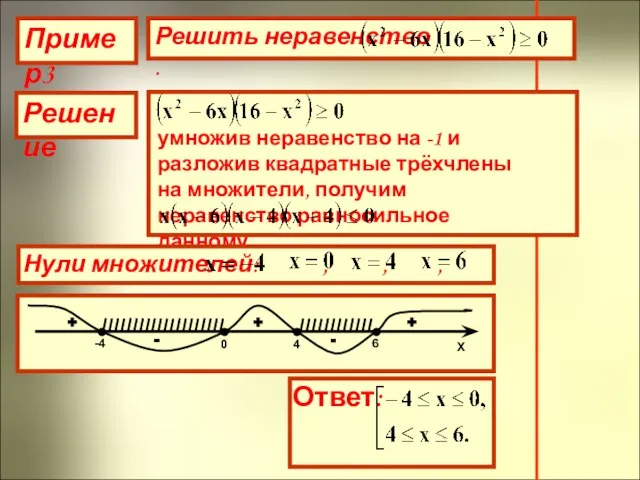
Пример3
Решение
умножив неравенство на -1 и разложив квадратные трёхчлены на множители, получим неравенство равносильное данному
+
+
-
-
+

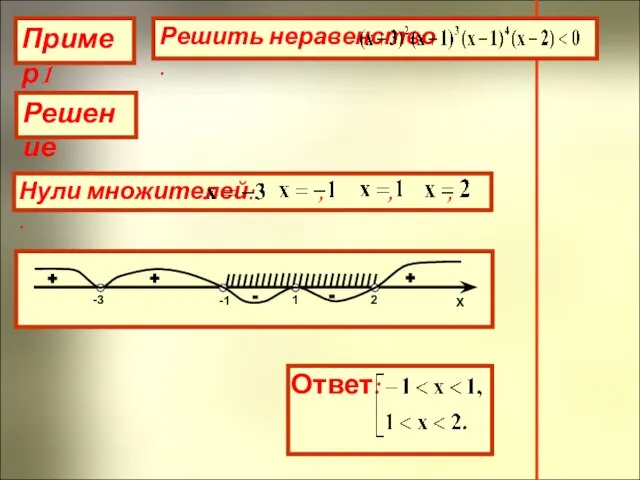
Пример4
Решение
+
+
+
+
-
-
-

3. Над промежутком справа от наибольшего нуля многочлена поставить знак «+», так как на этом промежутке все множители положительны. Затем, двигаясь справа налево, при переходе через очередной нуль, сменить знак на противоположный, если соответствующий этому нулю двучлен возведён в нечётную степень, и сохранить знак, если соответствующий этому нулю двучлен возведён в чётную степень.

Решение
+
+
-
-
+

+
-
-
+

+
+
-

умножив неравенство на -1 и разложив квадратные трёхчлены на множители, получим неравенство равносильное данному
+
-
+
-
+

+
-
+
-
+

Метод интервалов для решения неравенств вида
и , где и разлагаются в
произведения двучленов, где в числителе и знаменателе дроби имеются одинаковые двучлены .

+
-
-
+

+
+
+
-
-
-

Домашнее задание

ответы