Слайд 2Устно:
1.Решить уравнения:
1) 28x2=0; 2) x2=1 ⁄ 4 ; 3) x2- 25=0;

4) 4x2- 16=0;
5) x2+1=0
2.Найти такое положительное число m, чтобы данное выражение было квадратом суммы или разности:
x2+ 4x + m ; x2+ 16x + m; ; x2+ mx + 4; ;
x2-mx + 9
Слайд 3Для решения квадратных уравнений применяется метод выделения полного квадрата
Задача №1
Решить квадратное

уравнение
x2 + 2x - 3 =0.
Слайд 4Решение:
X2 + 2x-3=0.
1.Перенесём свободный член в правую часть уравнения (ИЗМЕНИВ,ЕГО ЗНАК НА

ПРОТИВОПОЛОЖНЫЙ)
X2 + 2x=3,
ЛЕВАЯ
2.Левую часть уравнения дополним до полного квадрата , X2 + 2∙x∙1 + 1
3.Но чтобы равенство оставалось верным, к правой части добавим такое же число , что мы дополнили к левой части
X2 + 2x∙1 + 1=3+1
X2 + 2x +1 = 4
Слайд 5Решение:
4.Левая часть уравнения является полным квадратом суммы (a + b)2=a2+ 2a+b2
Запишем
(x

+ 1)2=4
5.Значит можно применить теорему x2= d, где x1=√d, x2=-√d
x + 1=√4 или x +1=-√4
X +1=2 или x +1=-2
X=2-1 или х=-2-1
Х=1 или х=-3
Ответ: x1=1; x2=-3
Слайд 6Рассмотрим задачу №2 стр.115
Закрепление: решим №429 (1,3,5)

Слайд 71)X2- 4x-5=0
X2- 4x=5
X2- 2∙2x + 4=5+4
(x-2)2=9
X-2=√9 или x-2=-√9
x-2=3 или x-2=-3
x=5 или x=-1

Слайд 8X2+2x-15=0
X2 +2x =15
X2 +2x + 1=15+1
(x +1)2=16
X +1=√16 или x +1=-√16
X+1=4или x+1=-4
x=3
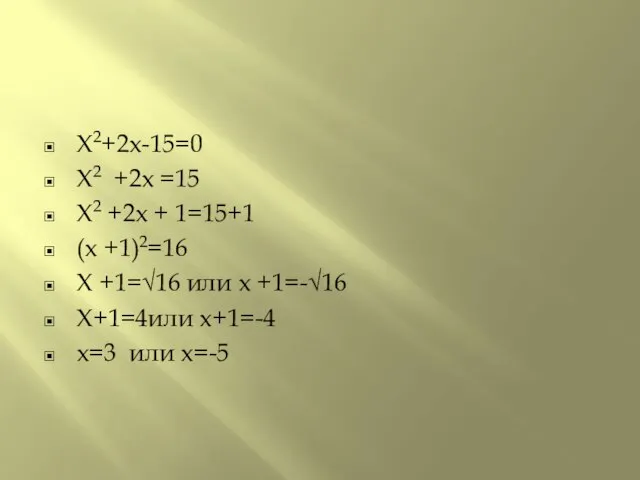
или x=-5
Слайд 9X2-6x+3=0
X2 -3∙2x =-3
X2 -6x + 9=-3+9
(x -3)2=6
X-3=√6или x-3=-√6
x=3 +√6 или x=3 -√6
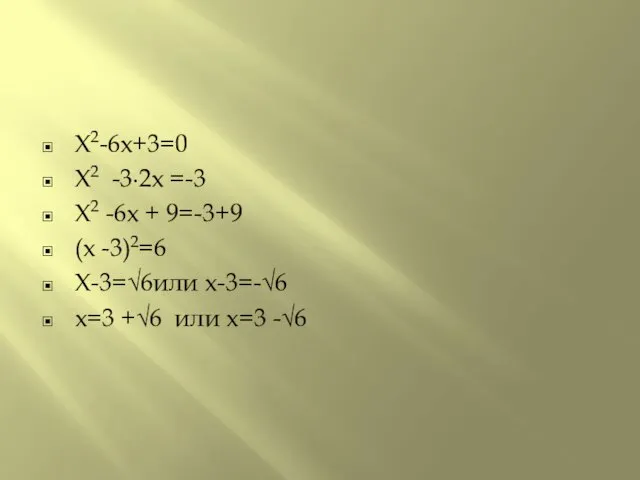
Слайд 10Рассмотрим задачу №3 стр.115
Закрепление №430(1)
9X2+6x-8=0
(3X)2 +3∙2x+1 =8 +1
9X2+6x + 1=9
(3x +1)2=9
3X+1=√9 или

3x+1=-√9
3x=3-1 или 3x=-3-1
3x=2 или 3x=-4
X=₂⁄3 или x= -₄⁄3
Слайд 11Что было трудно понять?
Как себя оцениваешь?
Главное из урока?
Дома:№429,430 повторить задачи стр.113,114,115

рассмотренные на уроках
Слайд 12 На дорожку
Ученик за 3 блокнота и 2 тетради уплатил 40 р,

другой ученик за 2 таких же блокнота и 4 тетради уплатил32р.
Сколько стоил блокнот и сколько стоила тетрадь?






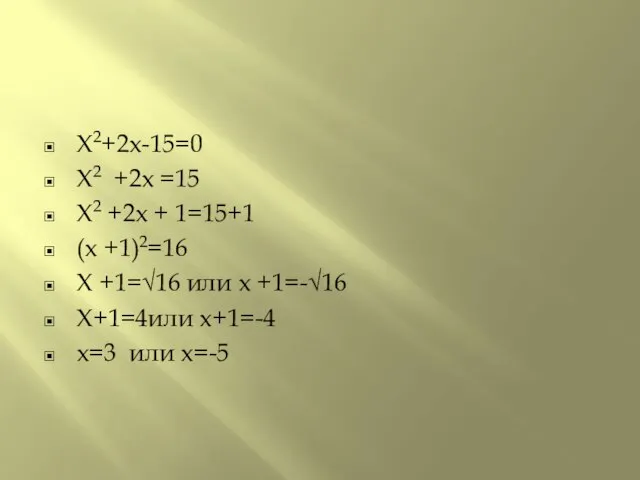
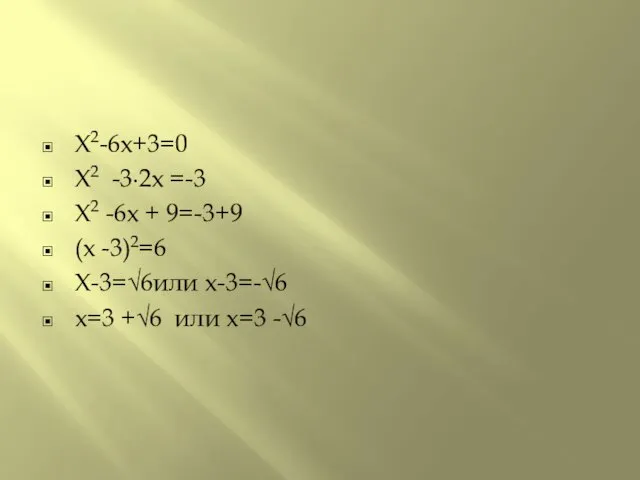



 Применение производной в различных науках
Применение производной в различных науках Корни натуральной степени из числа и их свойства
Корни натуральной степени из числа и их свойства Декартова система координат
Декартова система координат В стране занимательной Математики
В стране занимательной Математики Многогранники на службе у человека
Многогранники на службе у человека Аксиомы стереометрии
Аксиомы стереометрии Методика прикладных вычислений в конечных полях
Методика прикладных вычислений в конечных полях Многогранники в архитектуре
Многогранники в архитектуре Геометрия вокруг нас
Геометрия вокруг нас Презентация на тему Сложение и вычитание круглых десятков и однозначных чисел
Презентация на тему Сложение и вычитание круглых десятков и однозначных чисел  Теорема Пифагора
Теорема Пифагора Одночлен. Умножение
Одночлен. Умножение Логарифм числа и его свойства
Логарифм числа и его свойства электронный учебник по интеллектике в 5 классе. знакомство с вероятностью
электронный учебник по интеллектике в 5 классе. знакомство с вероятностью Неопределённый и определённый интеграл
Неопределённый и определённый интеграл Мультипликативная система индексов
Мультипликативная система индексов Циклоида, эпициклоида
Циклоида, эпициклоида Свойства и графики тригонометрических функций
Свойства и графики тригонометрических функций Экстремумы (1)
Экстремумы (1) Презентация по математике "Алгоритмы внутренних точек с приближенным решением вспомогательной задачи" -
Презентация по математике "Алгоритмы внутренних точек с приближенным решением вспомогательной задачи" -  Степень с натуральным показателем
Степень с натуральным показателем Геймификация образовательного процесса на уроках математики с использованием двигательной активности
Геймификация образовательного процесса на уроках математики с использованием двигательной активности Графический диктант Раскрытие скобок
Графический диктант Раскрытие скобок Что будет со мной, если буду питаться, как Дюймовочка?
Что будет со мной, если буду питаться, как Дюймовочка? Математическая викторина
Математическая викторина Итоговая диагностика. Математическая вертикаль. 8 класс
Итоговая диагностика. Математическая вертикаль. 8 класс Множества. (Задачи)
Множества. (Задачи) Таблица умножения и деления с числом 7
Таблица умножения и деления с числом 7