Слайд 2Дифференциальное уравнение
вынужденных колебаний

Слайд 3Если на балке рассматриваются 2 участка (АС, СВ), то решение уравнения (1)

необходимо составлять на каждом участке и использовать условия сопряжения на границе участков. Например, на 1 участке нет внешней нагрузки, поэтому уравнение (1) можно рассматривать как однородное и использовать решение однородного уравнения.
Слайд 4Решение дифференциального уравнения на 2-х участках

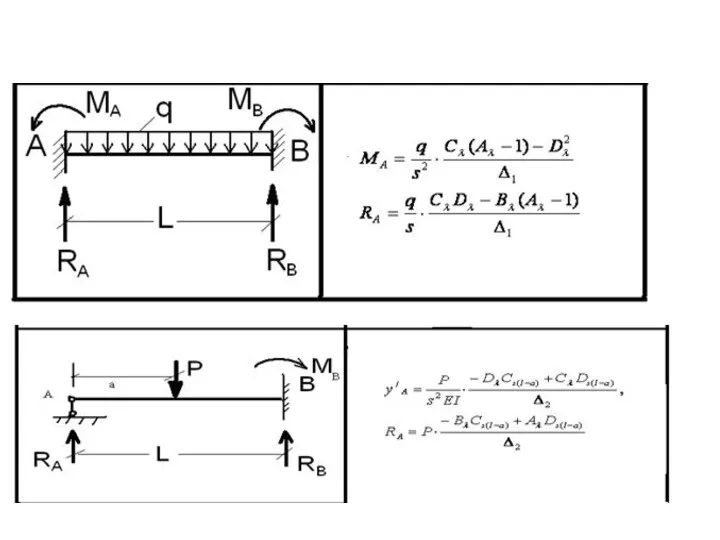
Слайд 5Формула для амплитудной функции прогибов на любом участке балки для случая действия

системы гармонических сосредоточенных сил, моментов и равномерно распределенных нагрузок
Слайд 6Формулы для амплитудных функций прогибов, изгибающих моментов и поперечных сил

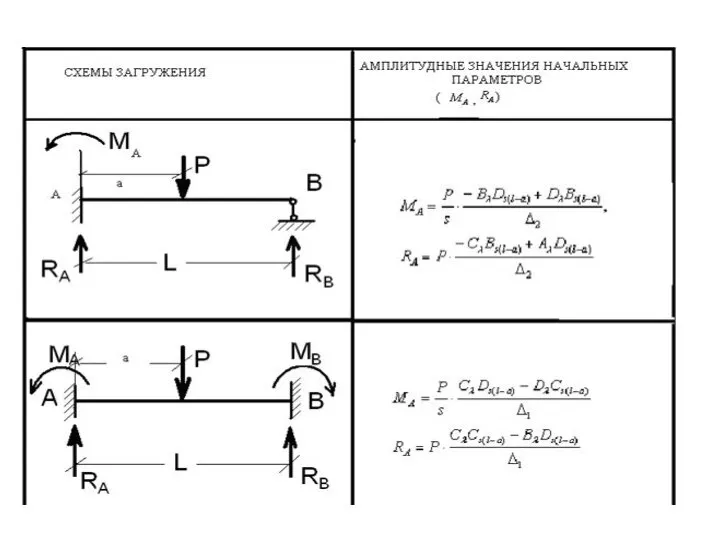
Слайд 7Граничные условия для балки шарнирно опертой двумя концами, находящейся под действием сосредоточенной

силы Р
∆М1 =0, ∆Q1=P, ∆qi =0
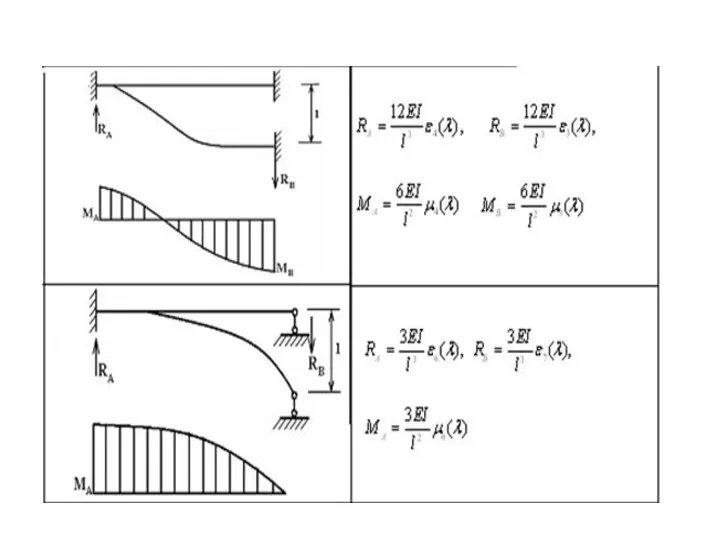
Слайд 8Случай вынужденных колебаний стержня – кинематическое возбуждение колебаний стержня, вызванное периодическим смещением
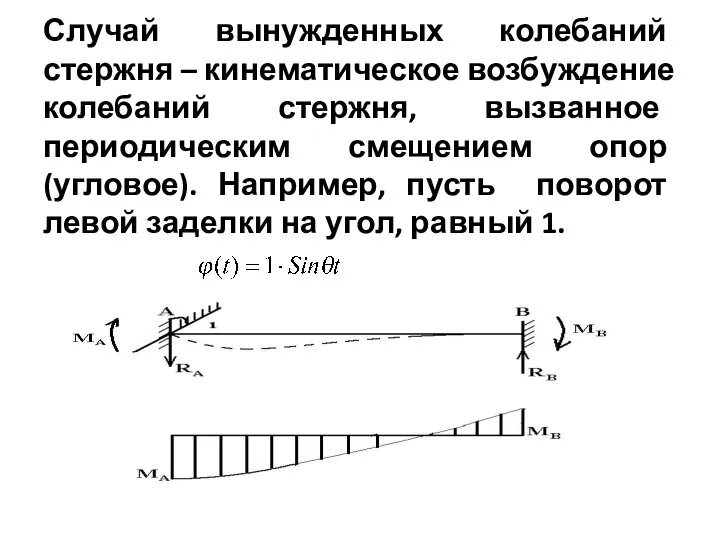
опор (угловое). Например, пусть поворот левой заделки на угол, равный 1.
Слайд 10Формулы для реактивных моментов и сил

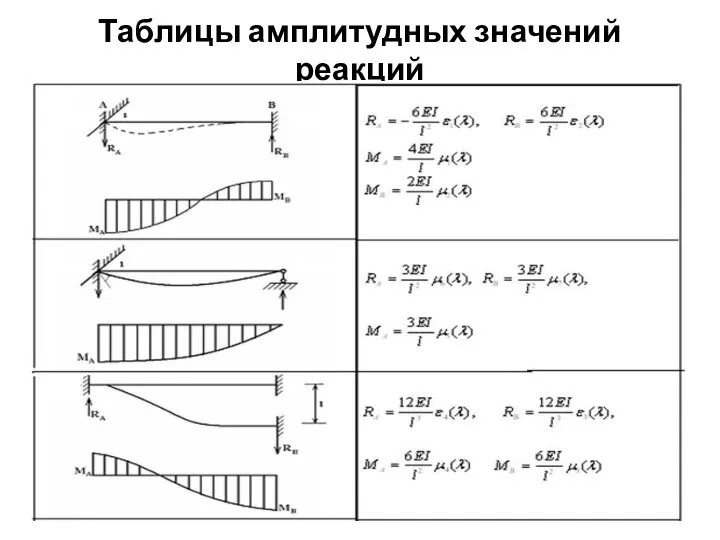
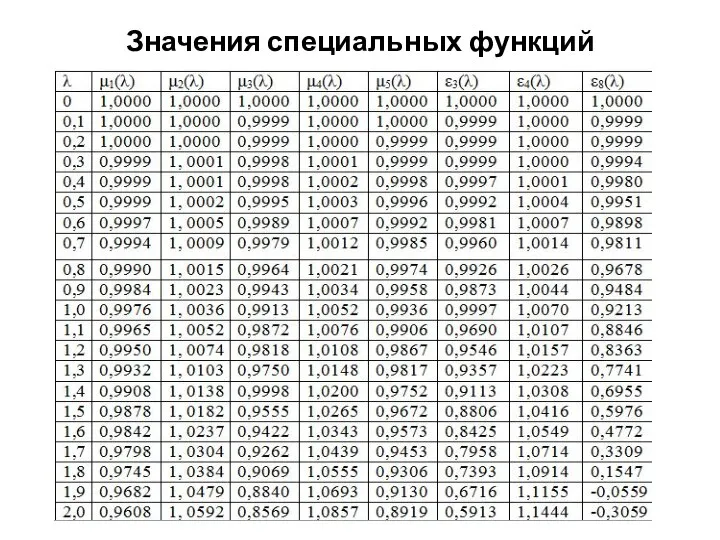
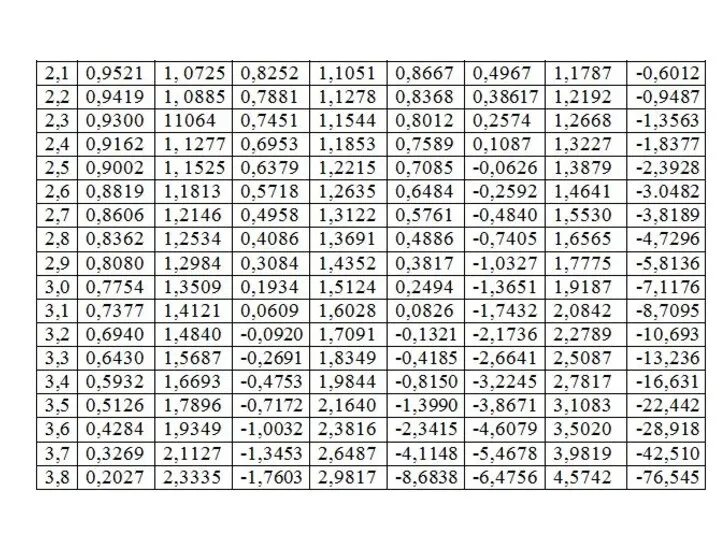
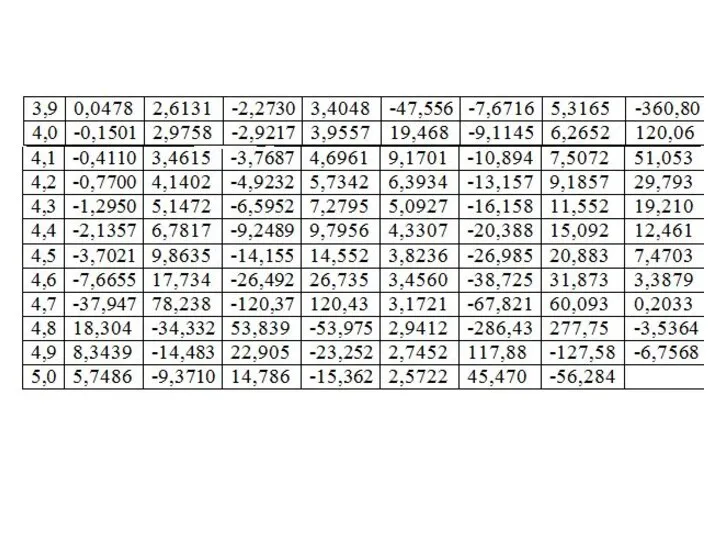
Слайд 11Таблицы амплитудных значений реакций
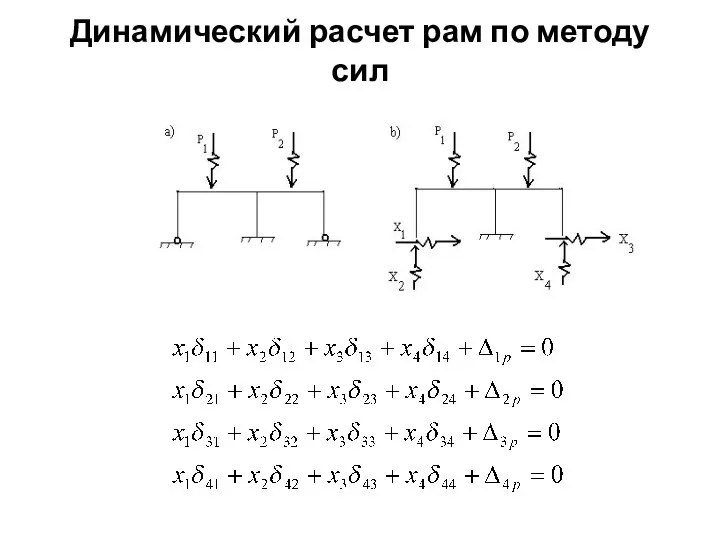
Слайд 20Динамический расчет рам по методу сил
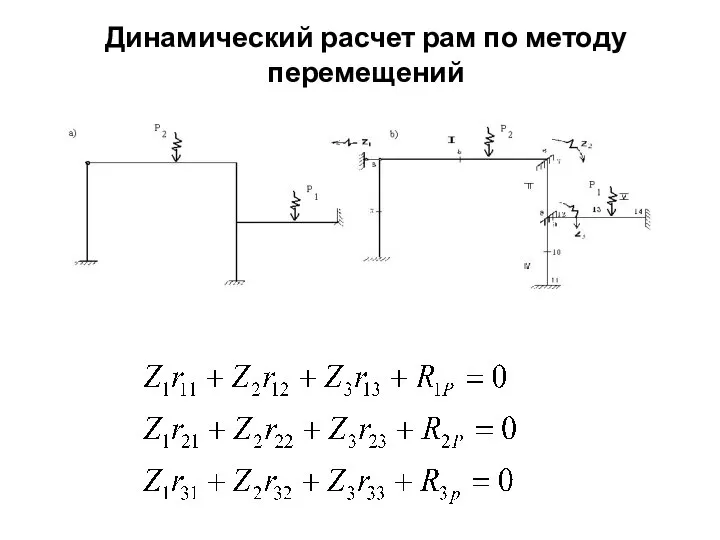
Слайд 21Динамический расчет рам по методу перемещений











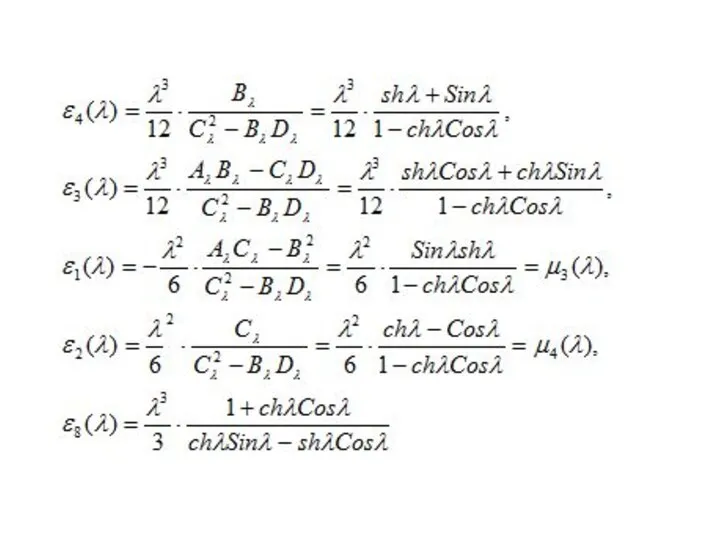


 Арифметический квадратный корень. Самостоятельная работа
Арифметический квадратный корень. Самостоятельная работа Параллельность прямых и плоскостей
Параллельность прямых и плоскостей Наибольшее и наименьшее значение функций
Наибольшее и наименьшее значение функций Презентация на тему Готфрид Вильгельм Лейбниц
Презентация на тему Готфрид Вильгельм Лейбниц 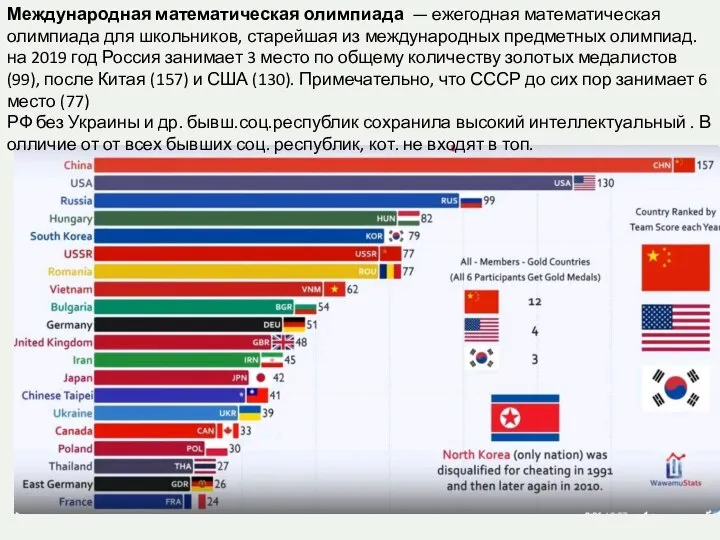 Международная математическая олимпиада
Международная математическая олимпиада Многоугольники в нашей жизни
Многоугольники в нашей жизни Формирование математических представлений, умений и навыков у дошкольников
Формирование математических представлений, умений и навыков у дошкольников Геометрический смысл производной. Производная и её геометрический смысл
Геометрический смысл производной. Производная и её геометрический смысл Согласные звуки [в],[ в’], буквы В, в
Согласные звуки [в],[ в’], буквы В, в Векторы в пространстве
Векторы в пространстве Пример записи решения задания к Части I РГР №1
Пример записи решения задания к Части I РГР №1 Презентация на тему Неопределенный интеграл
Презентация на тему Неопределенный интеграл  Статистический анализ случайных погрешностей
Статистический анализ случайных погрешностей Презентация на тему Понятие площади фигуры и ее измерение
Презентация на тему Понятие площади фигуры и ее измерение  Понятие области
Понятие области Проценты. 5 класс
Проценты. 5 класс Решение задач на применение свойств прямоугольного треугольника. 7 класс
Решение задач на применение свойств прямоугольного треугольника. 7 класс Окружность и круг
Окружность и круг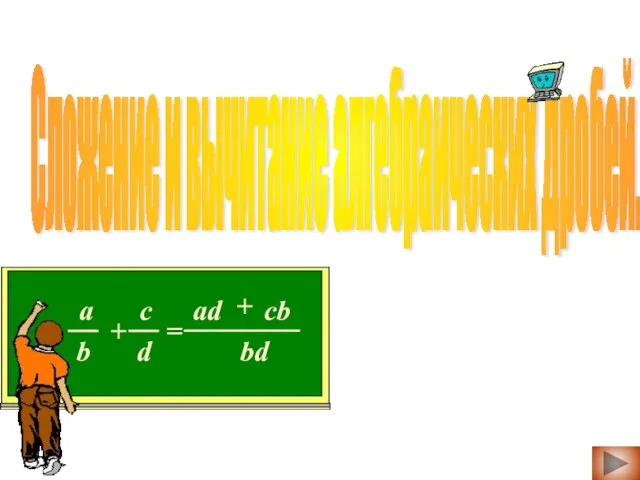 Сложение и вычитание алгебраических дробей
Сложение и вычитание алгебраических дробей Презентация на тему Формулы дифференцирования
Презентация на тему Формулы дифференцирования  Прибавить и вычесть 4
Прибавить и вычесть 4 Проценты. Устная работа
Проценты. Устная работа Реляционная алгебра
Реляционная алгебра Системы неравенств
Системы неравенств Задачи о зиме
Задачи о зиме Презентация на тему ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ
Презентация на тему ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ  Способы задания арифметической прогрессии
Способы задания арифметической прогрессии Презентация на тему ГИА 2013. Модуль АЛГЕБРА №7
Презентация на тему ГИА 2013. Модуль АЛГЕБРА №7