Содержание
- 2. План проекта: ввести понятие «золотое сечение» геометрическое построение «золотого сечения» построение правильного пятиугольника пентаграмма – символ
- 3. Алгебраическое построение «золотого сечения» АВ=а сводится к решению уравнения a:x=x:(a-x), где x=b, откуда x= =0,62a. Отношение
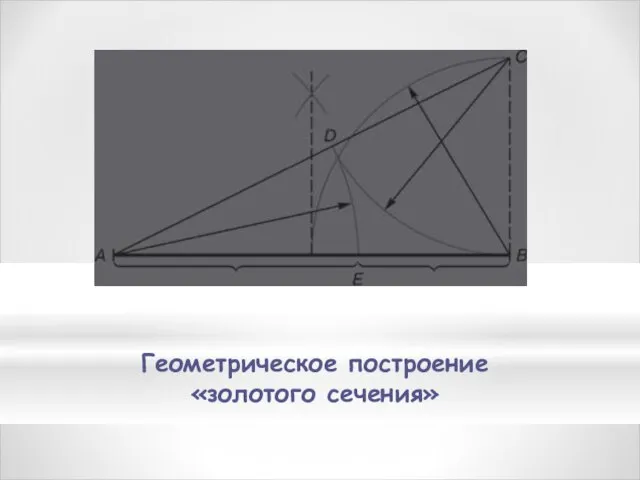
- 4. Геометрическое построение «золотого сечения»
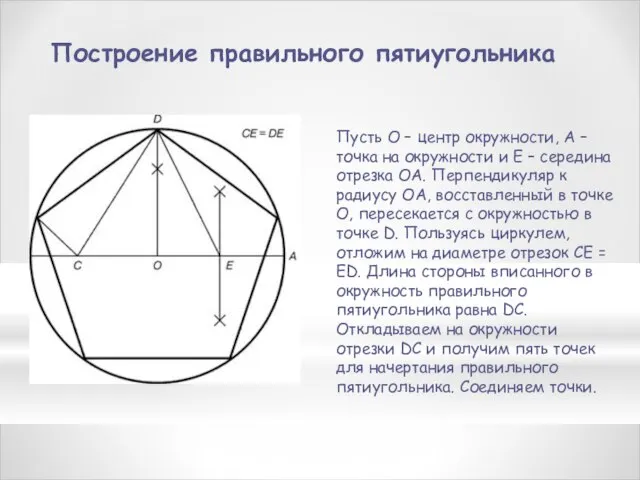
- 5. Построение правильного пятиугольника Пусть O – центр окружности, A – точка на окружности и Е –
- 6. Построение пентаграммы Соединяем углы полученного выше пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника
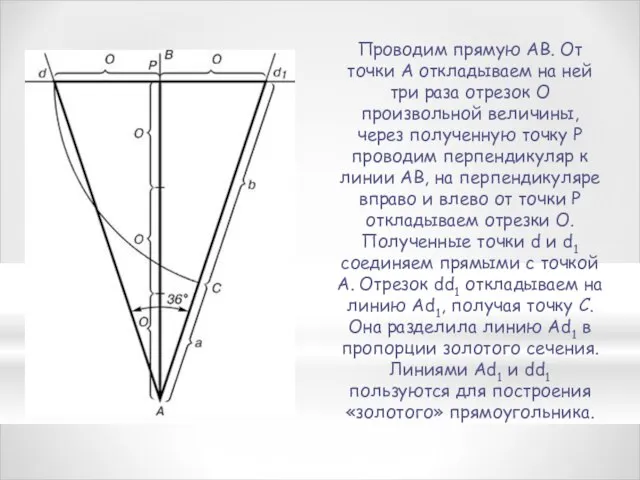
- 7. Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через
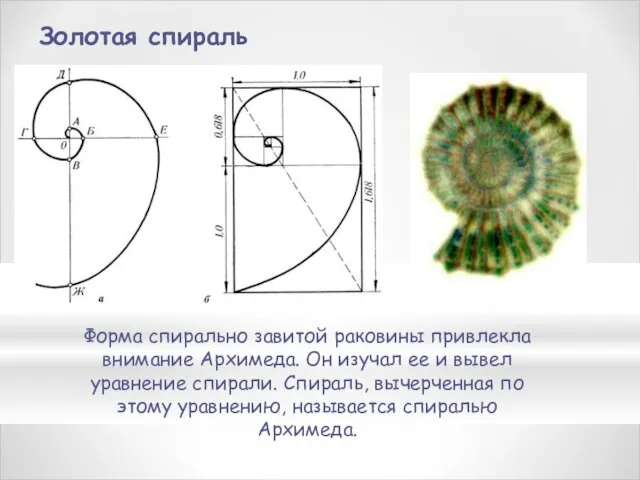
- 8. Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная
- 9. В расположении листьев на ветке, семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть,
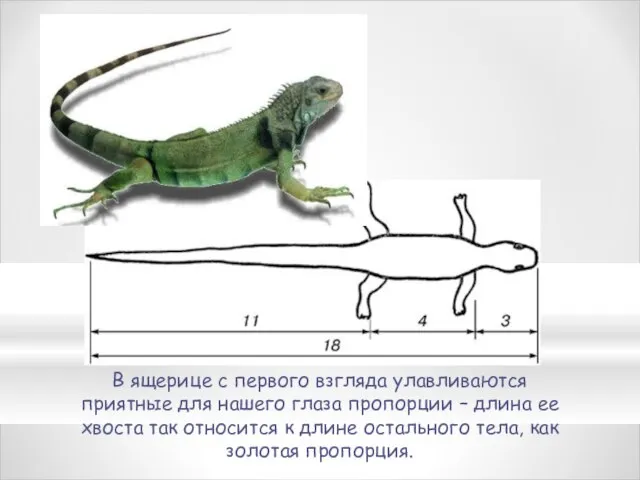
- 10. В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции – длина ее хвоста так
- 11. Портрет «Мона Лиза» (Джоконда) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на
- 12. На подготовительном эскизе Рафаэля проведены линии, идущие от смыслового центра композиции - точки, где пальцы воина
- 13. Статуя Поликлета «Дорифор» Отношение высот нижней и верхней частей, на которые статую делит пупок, равно золотому
- 14. Парфенон «Золотое сечение» многократно встречается при анализе геометрических соразмерностей Парфенона. В частности в отношении ширины фасада
- 15. ПРАКТИЧЕСКАЯ РАБОТА
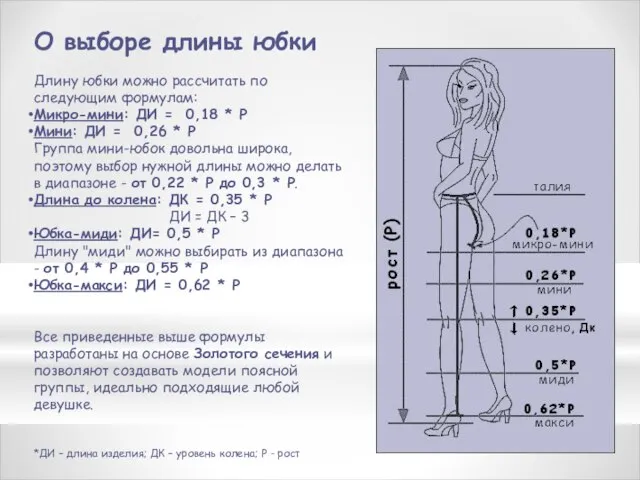
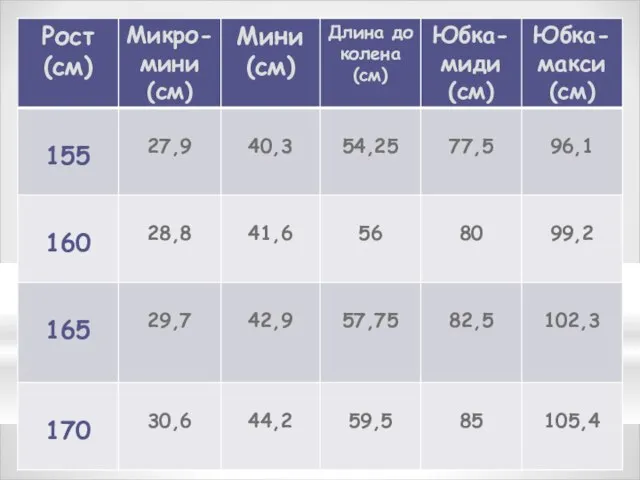
- 16. О выборе длины юбки Длину юбки можно рассчитать по следующим формулам: Микро-мини: ДИ = 0,18 *
- 19. Скачать презентацию









 Метод составления уравнений неголономной механики в задаче волнового твердотельного гироскопа
Метод составления уравнений неголономной механики в задаче волнового твердотельного гироскопа Как считать десятками
Как считать десятками Алгоритм принятия решения о выборе критерия оценки измерений
Алгоритм принятия решения о выборе критерия оценки измерений Векторы. Линейные операции над векторами. Разложение вектора по базису
Векторы. Линейные операции над векторами. Разложение вектора по базису Цели урока:
Цели урока: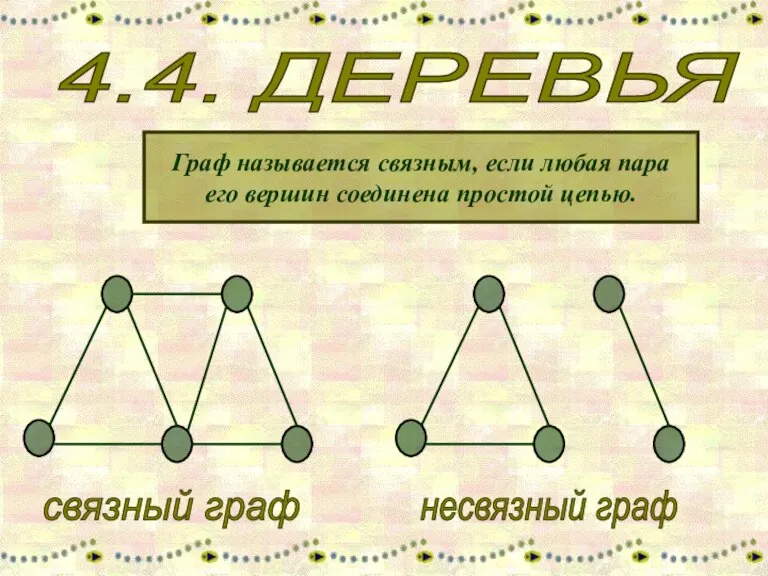 Деревья
Деревья Двойные интегралы в прямоугольной области
Двойные интегралы в прямоугольной области Признаки параллельных прямых
Признаки параллельных прямых Задачи на движение в одном направлении из одной точки
Задачи на движение в одном направлении из одной точки Задачи на нахождение элементов призмы
Задачи на нахождение элементов призмы Матрицы и действия над ними
Матрицы и действия над ними Треугольник
Треугольник Числа от 1 до 100. Сложение и вычитание
Числа от 1 до 100. Сложение и вычитание Статистические гипотезы и их проверка
Статистические гипотезы и их проверка Эллипсоид — поверхность в трёхмерном пространстве
Эллипсоид — поверхность в трёхмерном пространстве Неравенства. Решить систему неравенств
Неравенства. Решить систему неравенств Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Конус
Конус Таблица Шульте
Таблица Шульте УРОК МАТЕМАТИКИ В 5 кл. Учитель: Батычёк Т.Н.
УРОК МАТЕМАТИКИ В 5 кл. Учитель: Батычёк Т.Н. Числовое и буквенное выражения
Числовое и буквенное выражения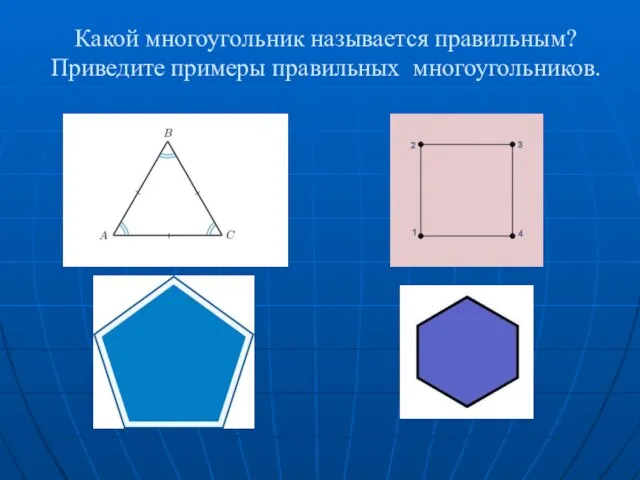 Какой многоугольник называется правильным? Приведите примеры правильных многоугольников
Какой многоугольник называется правильным? Приведите примеры правильных многоугольников Движение по окружности. Решение задач
Движение по окружности. Решение задач Системы линейных уравнений СЛУ
Системы линейных уравнений СЛУ Метод алгебраического сложения
Метод алгебраического сложения Экзаменационные задачи по дисциплине Процессы и аппараты
Экзаменационные задачи по дисциплине Процессы и аппараты ММК_Io66hWx
ММК_Io66hWx Повторение. Числа от 100 до 1000 (Урок 1)
Повторение. Числа от 100 до 1000 (Урок 1)